【好题必练】第19章 矩形、菱形与正方形全章重点巩固训练题(二)(含答案)
文档属性
| 名称 | 【好题必练】第19章 矩形、菱形与正方形全章重点巩固训练题(二)(含答案) | 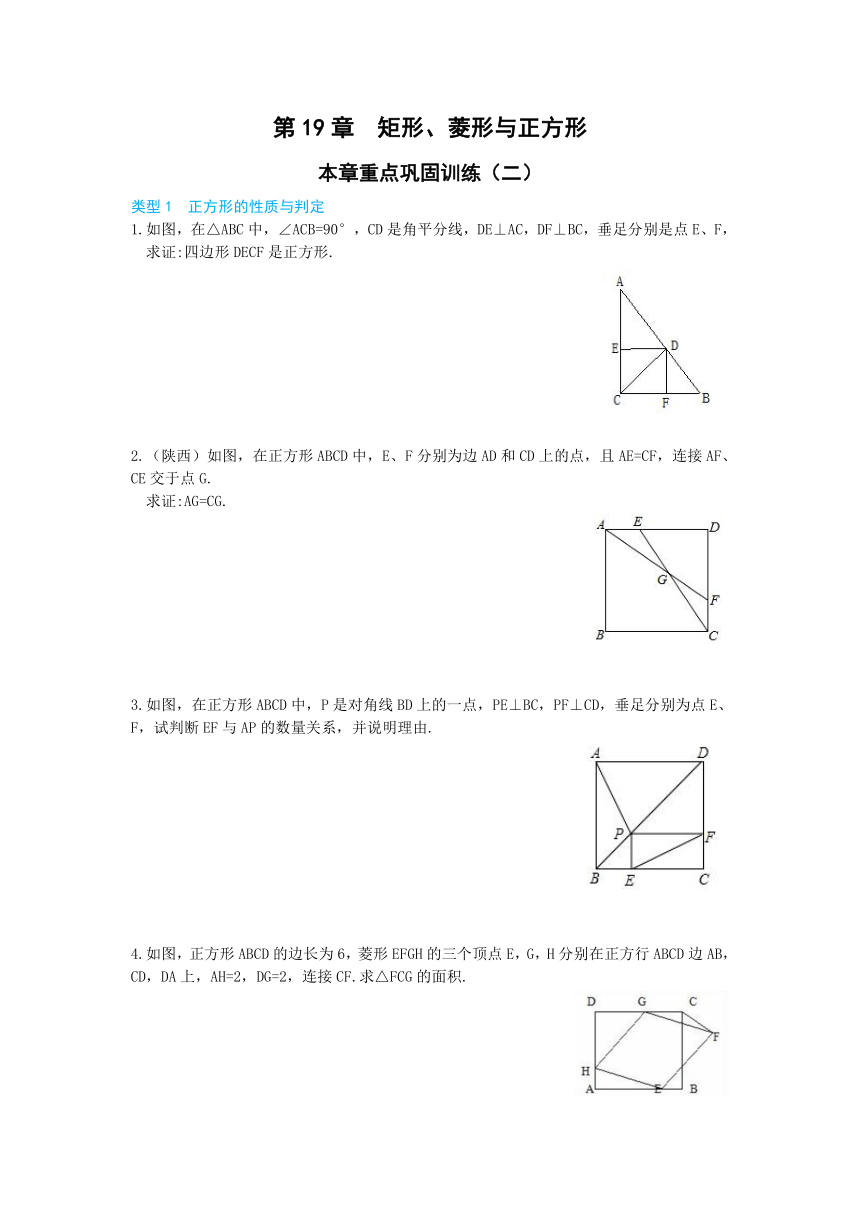 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 22:39:26 | ||
图片预览




文档简介
第19章 矩形、菱形与正方形
本章重点巩固训练(二) 类型1 正方形的性质与判定
1.如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是点E、F,求证:四边形DECF是正方形.
2.(陕西)如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.
求证:AG=CG.
3.如图,在正方形ABCD中,P是对角线BD上的一点,PE⊥BC,PF⊥CD,垂足分别为点E、F,试判断EF与AP的数量关系,并说明理由.
4.如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方行ABCD边AB,CD,DA上,AH=2,DG=2,连接CF.求△FCG的面积.
5.(江苏杭州)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
类型2 特殊平行四边形的探究性问题
6.如图,在△ABC中,点D、E、F分别在BC、AB、AC边上,且DE∥AC,DF∥AB.(1)如果∠ABC=90°,判断四边形AEDF的形状;
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
(1)试说明四边形AFED是平行四边形;
(2)当△ABC满足什么条件时,四边形AFED是矩形,说明理由;
(3)当△ABC满足什么条件时,四边形AFED是正方形?
(4)当△ABC满足什么条件时,四边形AFED不存在?
7.探究:如图1,在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD、AE,求证:△ACE≌△CBD.
应用:如图2,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD、EA,延长EA交CD于点G,求∠CGE的度数.
8.如图,在梯形ABCD中,AD∥BC,AB=CD,∠A=∠D,点E是线段AD上的一个动点(点E与点A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)探究四边形ECFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?为什么?
(3)若(2)中的菱形ECFH是正方形,请探究线段EF与线段BC的关系,并证明你的结论.
参 考 答 案
1.证明:∵CD是角平分线,DE⊥AC,DF⊥BC,
∴DE=DF,∠CED=∠CFD=90°.
∵ACB=90°,
∴四边形DECF是矩形,
又∵DE=DF,
∴四边形DECF是正方形.
2.证明∵四边形ABCD是正方形,
∴AD=CD.
∵AE=CF,
∴DE=DF,
又∠ADF=∠CDE,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中,
,
∴△AGE≌△CGF(AAS),
∴AG=CG.
3.解:EF=AP.理由如下:
∵PE⊥BC,PF⊥CD,四边形ABCD是正方形,
∴∠PEC=∠PFC=∠BCD=90°,
∴四边形PECF是矩形.
如图,连结PC,则PC=EF
∵P是正方形ABCD对角线上一点,
∴AD=CD,∠PDA=∠PDC.
在△PAD和△PCD中,
,
∴△PAD≌△PCD(S.A.S.),
∴PA=PC
∴EF=AP.
4.解:过点F作FM⊥CD交DC延长线于M,如下图,
∵四边形ABCD是正方形,
∴∠A=90°,AB=CD=6,DC∥AB,
∴∠CGE=∠AEG,
∴四边形EFGH是菱形,
∴EH=GF,GF∥HE,
∴∠FGE=∠HEG, ∴∠CGF=∠AEH,
在△FGM和△HEA中,, ∴△FGM≌△HEA(AAS), ∴FM=AH=2, ∵DG=2,DC=6, ∴GC=4, ∴△FCG的面积=GC·FM=×4×2=4.
5.解:(1)AG2=GE2-GF2.
理由:连结CG.
∵四辺形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形HGFC是矩形,
∴CF=GE.
在Rt△GFC中,CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上取一点M,使得AN=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,
∴∠GBN=30°,
∴∠MAB=∠ABM=15°,
∴∠AMN=30°,
∴BM=AM=2x,MN=x,
在Rt△ABN中,
∵AB2=AN2+BN2,
∴42=x2+(2x+x)2,
解得x=(负值舍去),
∴BN=,
∴BG=
6.解:(1)∵△ABD,△BCE,△FAC是等边三角形,
∴AB=DB,BC=BE,AC=AF,∠ABD=∠EBC=60°,
∴∠DBE=∠ABC.
在△BDE和△BAC中,
,
∴△DBE≌ABC(SAS),
∴DE=AC,
∴DE=AF.
同理可得DA=EF,
∴四边形AFED是平行四边形;
(2)当∠BAC=150°时,四边形ADEF是矩形.理由如下:
∵∠DAF=360°-∠DAB-∠BAC-∠CAF=360°-60°-150°-60°=90°,
∴平行四边形AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.理由如下:
由(2)可知,当∠BAC=150°时,四边形ADEF是矩形,
∵AB=AC,
∴矩形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
7.解:探究:∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=∠ABC.
∵BE=AD,
∴BE+BC=AD+AB,即CE=BD,
∴△ACE≌△CBD(S.A.S.).
应用:如图,连结AC,则△ABC是等边三角形.
由探究可知△ACE≌△CBD,
∴∠E=∠D.
∵∠BAE=∠DAG,
∴∠E+∠BAE=∠D+∠DAG,
∴∠ABC=∠CGE.
∵∠ABC=60?,
∴∠CGE=60?.
8.解:(1)四边形EGFH是平行四边形.理由如下:
∵G、F、H分别是BE、BC、CE的中点,
∴GF∥EH,GF=EH,
∴四边形EGFH是平行四边形.
(2)当点E是AD的中点时,四边形EGFH是菱形.
理由:在四边形ABCD中,∵点E是AD的中点,
∴AE=DE.
又∵∠A=∠D,AB=CD,
∴△ABE≌△DCE(S.A.S.),
∴BE=CE.
∵G、H分别是BE、CE的中点,
∴EG=EH.
又由(1)知四边形EGFH是平行四边形,
∴四边形EGFH是菱形.
(3)FF⊥BC,EF=BC.
证明:∵四边形EGFH是正方形,
∴EG=EH,∠BEC=90°.
∵G、H分别是BE、CE的中点,
∴BE=CE,
即△BCE是等腰直角三角形.
连结EF,易得△FBE≌△FCE,
∴∠BFE=∠CFE=90°,∠FBE=∠FCE=45°,
则EF=BF=CF,
∴EF⊥BC,且EF=BC.
本章重点巩固训练(二) 类型1 正方形的性质与判定
1.如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是点E、F,求证:四边形DECF是正方形.
2.(陕西)如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.
求证:AG=CG.
3.如图,在正方形ABCD中,P是对角线BD上的一点,PE⊥BC,PF⊥CD,垂足分别为点E、F,试判断EF与AP的数量关系,并说明理由.
4.如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方行ABCD边AB,CD,DA上,AH=2,DG=2,连接CF.求△FCG的面积.
5.(江苏杭州)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
类型2 特殊平行四边形的探究性问题
6.如图,在△ABC中,点D、E、F分别在BC、AB、AC边上,且DE∥AC,DF∥AB.(1)如果∠ABC=90°,判断四边形AEDF的形状;
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
(1)试说明四边形AFED是平行四边形;
(2)当△ABC满足什么条件时,四边形AFED是矩形,说明理由;
(3)当△ABC满足什么条件时,四边形AFED是正方形?
(4)当△ABC满足什么条件时,四边形AFED不存在?
7.探究:如图1,在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD、AE,求证:△ACE≌△CBD.
应用:如图2,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD、EA,延长EA交CD于点G,求∠CGE的度数.
8.如图,在梯形ABCD中,AD∥BC,AB=CD,∠A=∠D,点E是线段AD上的一个动点(点E与点A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)探究四边形ECFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?为什么?
(3)若(2)中的菱形ECFH是正方形,请探究线段EF与线段BC的关系,并证明你的结论.
参 考 答 案
1.证明:∵CD是角平分线,DE⊥AC,DF⊥BC,
∴DE=DF,∠CED=∠CFD=90°.
∵ACB=90°,
∴四边形DECF是矩形,
又∵DE=DF,
∴四边形DECF是正方形.
2.证明∵四边形ABCD是正方形,
∴AD=CD.
∵AE=CF,
∴DE=DF,
又∠ADF=∠CDE,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中,
,
∴△AGE≌△CGF(AAS),
∴AG=CG.
3.解:EF=AP.理由如下:
∵PE⊥BC,PF⊥CD,四边形ABCD是正方形,
∴∠PEC=∠PFC=∠BCD=90°,
∴四边形PECF是矩形.
如图,连结PC,则PC=EF
∵P是正方形ABCD对角线上一点,
∴AD=CD,∠PDA=∠PDC.
在△PAD和△PCD中,
,
∴△PAD≌△PCD(S.A.S.),
∴PA=PC
∴EF=AP.
4.解:过点F作FM⊥CD交DC延长线于M,如下图,
∵四边形ABCD是正方形,
∴∠A=90°,AB=CD=6,DC∥AB,
∴∠CGE=∠AEG,
∴四边形EFGH是菱形,
∴EH=GF,GF∥HE,
∴∠FGE=∠HEG, ∴∠CGF=∠AEH,
在△FGM和△HEA中,, ∴△FGM≌△HEA(AAS), ∴FM=AH=2, ∵DG=2,DC=6, ∴GC=4, ∴△FCG的面积=GC·FM=×4×2=4.
5.解:(1)AG2=GE2-GF2.
理由:连结CG.
∵四辺形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形HGFC是矩形,
∴CF=GE.
在Rt△GFC中,CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上取一点M,使得AN=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,
∴∠GBN=30°,
∴∠MAB=∠ABM=15°,
∴∠AMN=30°,
∴BM=AM=2x,MN=x,
在Rt△ABN中,
∵AB2=AN2+BN2,
∴42=x2+(2x+x)2,
解得x=(负值舍去),
∴BN=,
∴BG=
6.解:(1)∵△ABD,△BCE,△FAC是等边三角形,
∴AB=DB,BC=BE,AC=AF,∠ABD=∠EBC=60°,
∴∠DBE=∠ABC.
在△BDE和△BAC中,
,
∴△DBE≌ABC(SAS),
∴DE=AC,
∴DE=AF.
同理可得DA=EF,
∴四边形AFED是平行四边形;
(2)当∠BAC=150°时,四边形ADEF是矩形.理由如下:
∵∠DAF=360°-∠DAB-∠BAC-∠CAF=360°-60°-150°-60°=90°,
∴平行四边形AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.理由如下:
由(2)可知,当∠BAC=150°时,四边形ADEF是矩形,
∵AB=AC,
∴矩形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
7.解:探究:∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=∠ABC.
∵BE=AD,
∴BE+BC=AD+AB,即CE=BD,
∴△ACE≌△CBD(S.A.S.).
应用:如图,连结AC,则△ABC是等边三角形.
由探究可知△ACE≌△CBD,
∴∠E=∠D.
∵∠BAE=∠DAG,
∴∠E+∠BAE=∠D+∠DAG,
∴∠ABC=∠CGE.
∵∠ABC=60?,
∴∠CGE=60?.
8.解:(1)四边形EGFH是平行四边形.理由如下:
∵G、F、H分别是BE、BC、CE的中点,
∴GF∥EH,GF=EH,
∴四边形EGFH是平行四边形.
(2)当点E是AD的中点时,四边形EGFH是菱形.
理由:在四边形ABCD中,∵点E是AD的中点,
∴AE=DE.
又∵∠A=∠D,AB=CD,
∴△ABE≌△DCE(S.A.S.),
∴BE=CE.
∵G、H分别是BE、CE的中点,
∴EG=EH.
又由(1)知四边形EGFH是平行四边形,
∴四边形EGFH是菱形.
(3)FF⊥BC,EF=BC.
证明:∵四边形EGFH是正方形,
∴EG=EH,∠BEC=90°.
∵G、H分别是BE、CE的中点,
∴BE=CE,
即△BCE是等腰直角三角形.
连结EF,易得△FBE≌△FCE,
∴∠BFE=∠CFE=90°,∠FBE=∠FCE=45°,
则EF=BF=CF,
∴EF⊥BC,且EF=BC.
