【好题必练】第19章 矩形、菱形与正方形全章重点巩固训练题(一)(含答案)
文档属性
| 名称 | 【好题必练】第19章 矩形、菱形与正方形全章重点巩固训练题(一)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 22:38:11 | ||
图片预览



文档简介
第19章 矩形、菱形与正方形
本章重点巩固训练(一)
类型1 矩形的性质与判定
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
2.如图,在矩形ABCD中,点E是BC边上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
3.如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CF的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
4.如图,在矩形ABCD中,AB=4,AD=6,M、N分别是AB、CD的中点,P是AD上的点,且∠PNB=3∠CHN
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
5.如图,在□ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形BFDE是矩形.
类型2 菱形的性质与判定
6.在菱形ABCD中,点E,F分别为边CD,AD的中点,连接AE,CF.求证:△ADE≌△CDF.
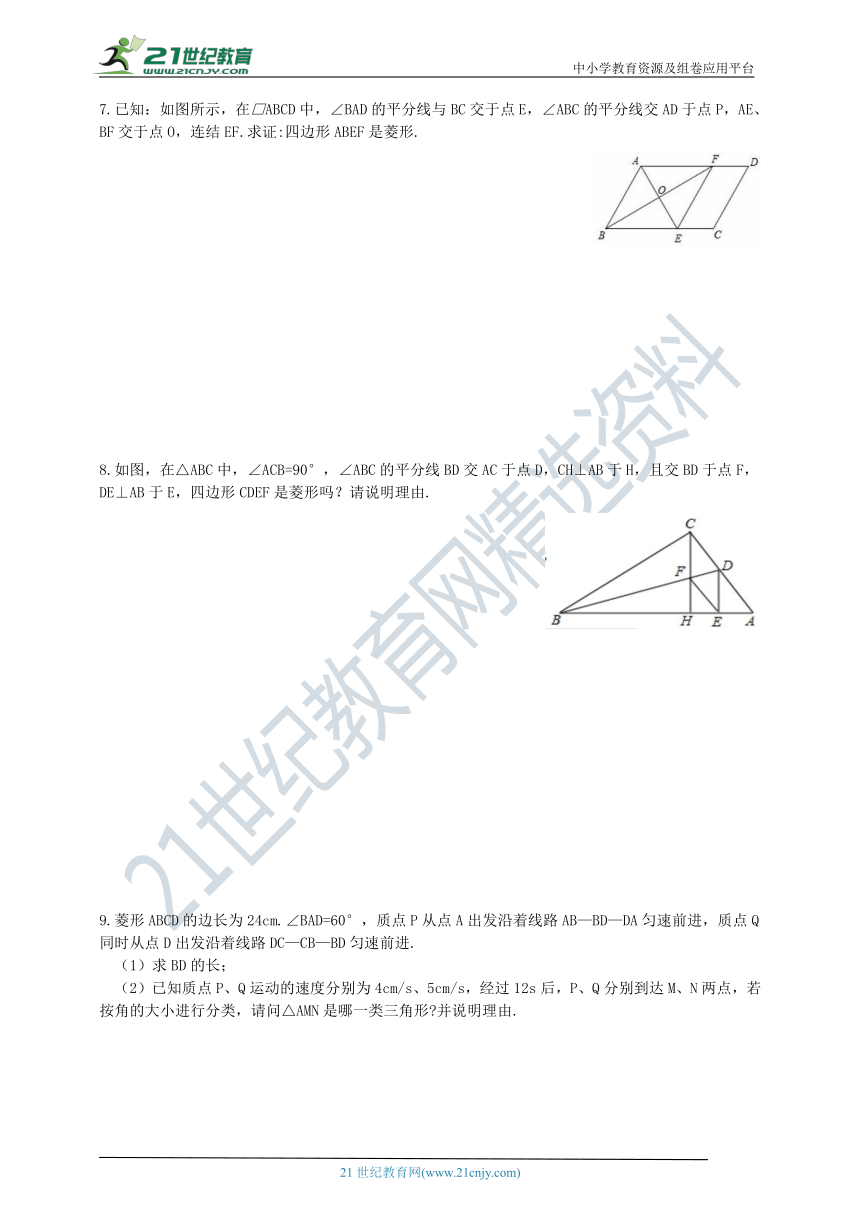
7.已知:如图所示,在□ABCD中,∠BAD的平分线与BC交于点E,∠ABC的平分线交AD于点P,AE、BF交于点O,连结EF.求证:四边形ABEF是菱形.
8.如图,在△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
9.菱形ABCD的边长为24cm.∠BAD=60°,质点P从点A出发沿着线路AB—BD—DA匀速前进,质点Q同时从点D出发沿着线路DC—CB—BD匀速前进.
(1)求BD的长;
(2)已知质点P、Q运动的速度分别为4cm/s、5cm/s,经过12s后,P、Q分别到达M、N两点,若按角的大小进行分类,请问△AMN是哪一类三角形?并说明理由.
8.如图,在菱形ABCD中,P是AB上一个动点(不与A,B重合),连接DP交对角线AC于E,连接BE.
(1)求证:∠APD=∠CBE;
(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?
参 考 答 案
1.证明:∵四边形ABCD为矩形,
∴∠ADC=∠BCD=90°
AC=BD,OD=BD,OC=AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,即∠EDO=∠FCO.
又∵DE=CF,
∴△ODE≌△OCF(SAS),
∴OE=OF.
2.证明:∵四边形ABCD是矩形,
∴AB=CD,AD∥BC,∠B=90°.
∵DF⊥AE,
∴∠AFD=∠B=90°.
∵AD∥BC,
∴∠DAE=∠AEB.
又∵AD=AE,
∴△ADF≌△EAB(AAS),
∴DF=AB,
∴DF=DC.
3.(1)证明:∵点E是AD的中点,∴AE=DE.
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE.
∴∠EAF≌△EDC.∴AF=DC.
∵AF=BD,
∴BD=DC,即D是BC的中点.
(2)四边形AFBD是矩形.证明如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,又由(1)可知D是BC的中点,
∴AD⊥BC.
∴四边形AFBD是矩形.
4.(1)证明:∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN//BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN.
(2)如图,连结AN.
根据矩形的对称性可知∠PAN=∠CBN,
由(1),知∠PNM=2∠CBN=2∠PAN.
∵MN∥AD.
∴∠PAN=∠ANM,
∴∠PAN=∠PNA,
∴AP=PN.
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2.
设AP=x,则PD=6-x,PN=x.
在Rt△PDN中,PD2+DN2=PN2,
∴(6-x)2+22=x2,解得x=.
即AP的长为.
5.证明:(1)在ABCD中,AB=CD,∠A=∠C,AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,
∴∠CDF=∠CDB,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(A.S.A.).
(2)由(1),知△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°,
∴平行四边形BFDE是矩形.
6.证明:∵四边形ABCD为菱形,
∴AD=CD,
?∵点E,F分别为边CD,AD的中点,
∴AD-2DF,CD=2DE,
∴DE=DF,? ?在△ADE和△CDF中,, ?∴△ADE≌△CDF(SAS).
7.证明:∵四边形ABCD是平行四过形,
∴AD∥BC,
∴∠DAE=∠AEB.
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,
同理,AB=AF,
∴AF=BE.
又∵AF∥BE,
∴四边形ABEF是平行四边形,
又∵AB=AF,
∴四边形ABEF是菱形.
8.解:四边形CDEF是菱形.
证明如下:∵BD平分∠ABC,DC⊥BC,DE⊥AB,
∴DC=DE,又BD=BD,
∴Rt△BCD≌Rt△BED(HL),
∴∠BDC=∠BDE.又FD= FD,
∴△CDF≌△EDF(SAS),
∴∠FCD=∠FED.
∵CH⊥AB,DE⊥AB,
∴CH∥DE,
∴∠HFE=∠FED.
∴∠HFE=∠FCD,
∴FE∥CD,
∴四边形FEDC是平行四边形,又DC=DE,
∴□FEDC是菱形.
9.解:(1)∵菱形ABCD中,∠BAD=60°,
∴△ABD为等边三角形,
∴BD=AB=24cm
(2)∵vp=4cm/s,
∴sp=vpt=48cm.
又∵BD=AB=24cm,
∴点P到达点D,即点M与点D重合.
∵vQ=5cm/s,
∴sQ=vQt=60cm,
∴点N在BD的中点,
∴∠ANM=90°,即△AMN为直角三角形.
10. 解:(1)∵四边形ABCD是菱形,
∴BC=CD,AC平分∠BCD.
∵CE=CE,
∴△BCE≌△DCE,
∴∠EBC=∠EDC.
又∵AB∥DC,∴∠APD=∠CDP,
∴∠EBC=∠APD.
(2)当P点运动到AB边的中点时,S△ADP=S菱形ABCD.
理由:连接DB,如下图.
∵∠DAB=60°,AD=AB,
∴△ABD是等边三角形.
∵P是AB边的中点,
∴DP⊥AB,
∴S△ADP=AP·DP,S菱形ABCD=AB·DP.
∵AP=AB,
∴S△ADP=×AB·DP=S菱形ABCD,
即△ADP的面积等于菱形ABCD面积的.
本章重点巩固训练(一)
类型1 矩形的性质与判定
1.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
2.如图,在矩形ABCD中,点E是BC边上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.
3.如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CF的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
4.如图,在矩形ABCD中,AB=4,AD=6,M、N分别是AB、CD的中点,P是AD上的点,且∠PNB=3∠CHN
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
5.如图,在□ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形BFDE是矩形.
类型2 菱形的性质与判定
6.在菱形ABCD中,点E,F分别为边CD,AD的中点,连接AE,CF.求证:△ADE≌△CDF.
7.已知:如图所示,在□ABCD中,∠BAD的平分线与BC交于点E,∠ABC的平分线交AD于点P,AE、BF交于点O,连结EF.求证:四边形ABEF是菱形.
8.如图,在△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
9.菱形ABCD的边长为24cm.∠BAD=60°,质点P从点A出发沿着线路AB—BD—DA匀速前进,质点Q同时从点D出发沿着线路DC—CB—BD匀速前进.
(1)求BD的长;
(2)已知质点P、Q运动的速度分别为4cm/s、5cm/s,经过12s后,P、Q分别到达M、N两点,若按角的大小进行分类,请问△AMN是哪一类三角形?并说明理由.
8.如图,在菱形ABCD中,P是AB上一个动点(不与A,B重合),连接DP交对角线AC于E,连接BE.
(1)求证:∠APD=∠CBE;
(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的,为什么?
参 考 答 案
1.证明:∵四边形ABCD为矩形,
∴∠ADC=∠BCD=90°
AC=BD,OD=BD,OC=AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,即∠EDO=∠FCO.
又∵DE=CF,
∴△ODE≌△OCF(SAS),
∴OE=OF.
2.证明:∵四边形ABCD是矩形,
∴AB=CD,AD∥BC,∠B=90°.
∵DF⊥AE,
∴∠AFD=∠B=90°.
∵AD∥BC,
∴∠DAE=∠AEB.
又∵AD=AE,
∴△ADF≌△EAB(AAS),
∴DF=AB,
∴DF=DC.
3.(1)证明:∵点E是AD的中点,∴AE=DE.
∵AF∥BC,
∴∠AFE=∠DCE,∠FAE=∠CDE.
∴∠EAF≌△EDC.∴AF=DC.
∵AF=BD,
∴BD=DC,即D是BC的中点.
(2)四边形AFBD是矩形.证明如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,又由(1)可知D是BC的中点,
∴AD⊥BC.
∴四边形AFBD是矩形.
4.(1)证明:∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN//BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN.
(2)如图,连结AN.
根据矩形的对称性可知∠PAN=∠CBN,
由(1),知∠PNM=2∠CBN=2∠PAN.
∵MN∥AD.
∴∠PAN=∠ANM,
∴∠PAN=∠PNA,
∴AP=PN.
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2.
设AP=x,则PD=6-x,PN=x.
在Rt△PDN中,PD2+DN2=PN2,
∴(6-x)2+22=x2,解得x=.
即AP的长为.
5.证明:(1)在ABCD中,AB=CD,∠A=∠C,AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,
∴∠CDF=∠CDB,
∴∠ABE=∠CDF.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(A.S.A.).
(2)由(1),知△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形BFDE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°,
∴平行四边形BFDE是矩形.
6.证明:∵四边形ABCD为菱形,
∴AD=CD,
?∵点E,F分别为边CD,AD的中点,
∴AD-2DF,CD=2DE,
∴DE=DF,? ?在△ADE和△CDF中,, ?∴△ADE≌△CDF(SAS).
7.证明:∵四边形ABCD是平行四过形,
∴AD∥BC,
∴∠DAE=∠AEB.
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,
同理,AB=AF,
∴AF=BE.
又∵AF∥BE,
∴四边形ABEF是平行四边形,
又∵AB=AF,
∴四边形ABEF是菱形.
8.解:四边形CDEF是菱形.
证明如下:∵BD平分∠ABC,DC⊥BC,DE⊥AB,
∴DC=DE,又BD=BD,
∴Rt△BCD≌Rt△BED(HL),
∴∠BDC=∠BDE.又FD= FD,
∴△CDF≌△EDF(SAS),
∴∠FCD=∠FED.
∵CH⊥AB,DE⊥AB,
∴CH∥DE,
∴∠HFE=∠FED.
∴∠HFE=∠FCD,
∴FE∥CD,
∴四边形FEDC是平行四边形,又DC=DE,
∴□FEDC是菱形.
9.解:(1)∵菱形ABCD中,∠BAD=60°,
∴△ABD为等边三角形,
∴BD=AB=24cm
(2)∵vp=4cm/s,
∴sp=vpt=48cm.
又∵BD=AB=24cm,
∴点P到达点D,即点M与点D重合.
∵vQ=5cm/s,
∴sQ=vQt=60cm,
∴点N在BD的中点,
∴∠ANM=90°,即△AMN为直角三角形.
10. 解:(1)∵四边形ABCD是菱形,
∴BC=CD,AC平分∠BCD.
∵CE=CE,
∴△BCE≌△DCE,
∴∠EBC=∠EDC.
又∵AB∥DC,∴∠APD=∠CDP,
∴∠EBC=∠APD.
(2)当P点运动到AB边的中点时,S△ADP=S菱形ABCD.
理由:连接DB,如下图.
∵∠DAB=60°,AD=AB,
∴△ABD是等边三角形.
∵P是AB边的中点,
∴DP⊥AB,
∴S△ADP=AP·DP,S菱形ABCD=AB·DP.
∵AP=AB,
∴S△ADP=×AB·DP=S菱形ABCD,
即△ADP的面积等于菱形ABCD面积的.
