【好题必练】第19章 矩形、菱形与正方形全章难点突破(二):菱形的性质和判定专题训练题(含答案)
文档属性
| 名称 | 【好题必练】第19章 矩形、菱形与正方形全章难点突破(二):菱形的性质和判定专题训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览


文档简介
第19章 矩形、菱形与正方形
难点突破专题训练(六)
菱形的性质和判定
突破点1 与菱形性质有关的探究题
1.如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某点连成一条新的线段,猜想并证明它和图中已有的某条线段相等(只需证明一组线段相等即可).
(1)连接 ;
(2)猜想: = ;
(3)证明(说明:写出证明过程的重要依据).
/
2.如图,菱形ABCD中,∠B=60°,AB=2,点E、F分别是AB、AD上的动点,且满足BE=AF,接连EF、EC、CF.
(1)求证:△EFC是等边三角形;
(2)试探究△AEF的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
/
突破点2 菱形性质与判定的综合
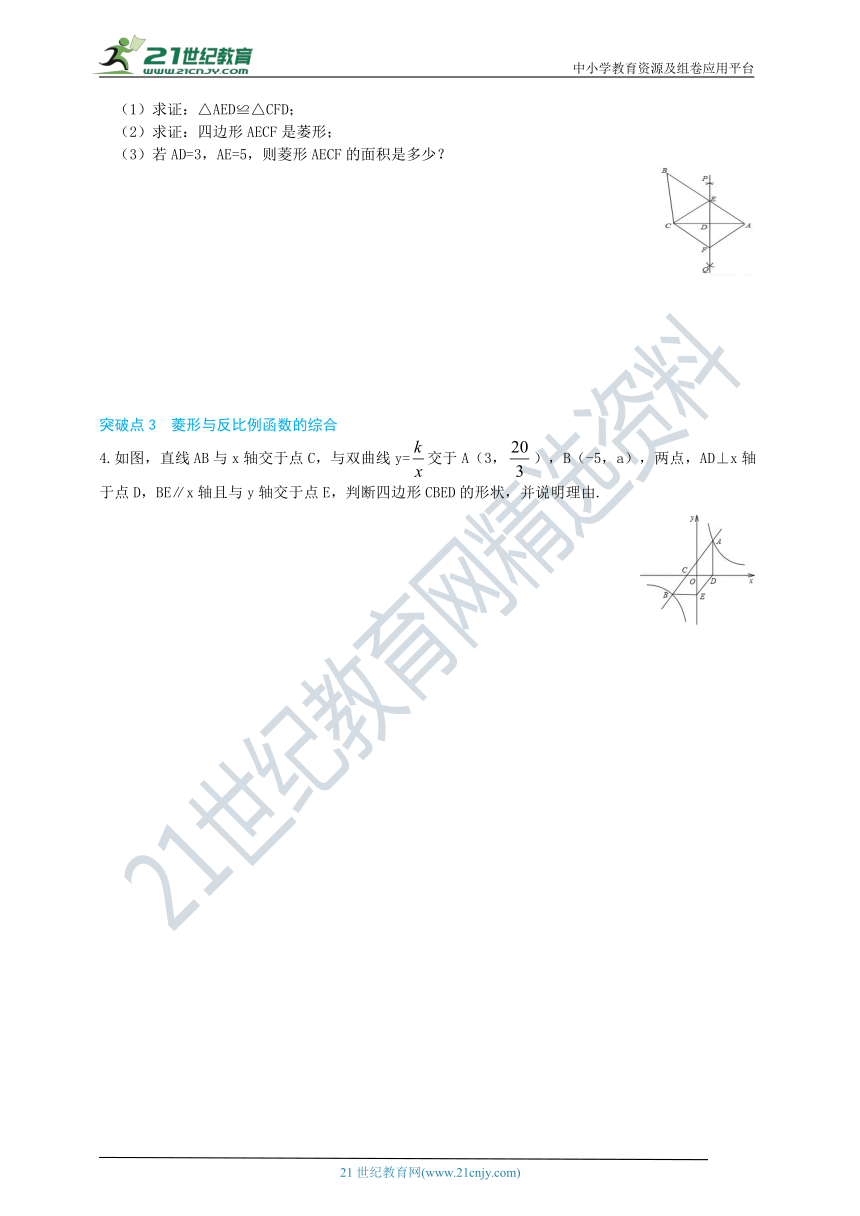
3.如图,已知△ABC,直线PQ垂直平分边AC,与边AB交于点E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是萎形;
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
/
突破点3 菱形与反比例函数的综合
4.如图,直线AB与x轴交于点C,与双曲线y=交于A(3,),B(-5,a),两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
/
参 考 答 案
1.解:(1)如下图,连接AF.
(2)AF=AE.
(3)四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABF=∠ADE.
在△ABF和AADE中,,
∴△ABF≌△ADE,
∴AF=AE.
/
2.(1)证明:连接AC,
/
∵四边形ABCD是菱形,
∴∠1=∠2=∠BAD,AD∥BC,AB=BC,
∴∠B+∠BAD=180°,
∵∠B=60°,
∴∠BAD=120°,
∴∠1=∠2=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴AC=BC,
在△AFC和△BEC中,,
∴△AFC≌△BEC(SAS),
∴FC=EC,∠4=∠3,
∵AD∥CB,
∴∠4+∠5=∠2=60°,
∴∠3+∠5=60°,
∴△EFC是等边三角形;
(2)△AEF的周长有最小值,
理由:当CE⊥AB时CE最短,由△CEF是等边三角形,
∴EF也是最短的.
CE是边长为2等边△ABC的高,
∴CE=,EF=,
∴AE+AF+EF=2+.
∴△AEF周长的最小值为:2+.
3.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD.
∵CF∥AB,
∴∠EAC=∠FCA,∠CFD=∠AED.
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA).
(2)∵△AED≌△CFD,
∴AE=CF.
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形
(3)∵AD=3,AE=5,
∴根据勾股定理得:ED=4,
∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24,
∴菱形AECF的面积是24.
4.解:四边形CBED是菱形.
∵双曲线y=过A(3,),
∴k=20.
把B(-5,a)代人y=,
得a=-4.
∴点B的坐标是(-5,-4).
∵AD⊥x轴于D,
∴D(3,0).
设直线AB的解析式为y=mx+n,
将A(3,),B(-5,-4)代入得:
,
解得m=,n=,
∴直线AB的解析式为y=x+,
∴点C的坐标是(-2,0).
∵BE∥x轴,
∴点E的坐标是(0,-4),
而CD=5,BE=5,且BE∥CD,
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED==5,
∴ED=CD,
∴□CBED是菱形.
/
难点突破专题训练(六)
菱形的性质和判定
突破点1 与菱形性质有关的探究题
1.如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某点连成一条新的线段,猜想并证明它和图中已有的某条线段相等(只需证明一组线段相等即可).
(1)连接 ;
(2)猜想: = ;
(3)证明(说明:写出证明过程的重要依据).
/
2.如图,菱形ABCD中,∠B=60°,AB=2,点E、F分别是AB、AD上的动点,且满足BE=AF,接连EF、EC、CF.
(1)求证:△EFC是等边三角形;
(2)试探究△AEF的周长是否存在最小值?如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
/
突破点2 菱形性质与判定的综合
3.如图,已知△ABC,直线PQ垂直平分边AC,与边AB交于点E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是萎形;
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
/
突破点3 菱形与反比例函数的综合
4.如图,直线AB与x轴交于点C,与双曲线y=交于A(3,),B(-5,a),两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
/
参 考 答 案
1.解:(1)如下图,连接AF.
(2)AF=AE.
(3)四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∴∠ABF=∠ADE.
在△ABF和AADE中,,
∴△ABF≌△ADE,
∴AF=AE.
/
2.(1)证明:连接AC,
/
∵四边形ABCD是菱形,
∴∠1=∠2=∠BAD,AD∥BC,AB=BC,
∴∠B+∠BAD=180°,
∵∠B=60°,
∴∠BAD=120°,
∴∠1=∠2=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴AC=BC,
在△AFC和△BEC中,,
∴△AFC≌△BEC(SAS),
∴FC=EC,∠4=∠3,
∵AD∥CB,
∴∠4+∠5=∠2=60°,
∴∠3+∠5=60°,
∴△EFC是等边三角形;
(2)△AEF的周长有最小值,
理由:当CE⊥AB时CE最短,由△CEF是等边三角形,
∴EF也是最短的.
CE是边长为2等边△ABC的高,
∴CE=,EF=,
∴AE+AF+EF=2+.
∴△AEF周长的最小值为:2+.
3.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD.
∵CF∥AB,
∴∠EAC=∠FCA,∠CFD=∠AED.
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA).
(2)∵△AED≌△CFD,
∴AE=CF.
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形
(3)∵AD=3,AE=5,
∴根据勾股定理得:ED=4,
∴EF=8,AC=6,
∴S菱形AECF=8×6÷2=24,
∴菱形AECF的面积是24.
4.解:四边形CBED是菱形.
∵双曲线y=过A(3,),
∴k=20.
把B(-5,a)代人y=,
得a=-4.
∴点B的坐标是(-5,-4).
∵AD⊥x轴于D,
∴D(3,0).
设直线AB的解析式为y=mx+n,
将A(3,),B(-5,-4)代入得:
,
解得m=,n=,
∴直线AB的解析式为y=x+,
∴点C的坐标是(-2,0).
∵BE∥x轴,
∴点E的坐标是(0,-4),
而CD=5,BE=5,且BE∥CD,
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED==5,
∴ED=CD,
∴□CBED是菱形.
/
