【好题必练】第20章 数据的整理与初步处理全章重点巩固训练题(含答案)
文档属性
| 名称 | 【好题必练】第20章 数据的整理与初步处理全章重点巩固训练题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 22:52:05 | ||
图片预览


文档简介
第20章 数据的整理与初步处理
本章重点巩固训练
类型1 平均数
1.体育课上全班女生进行百米测试,达标成绩为18秒,现以达标成绩为标准,成绩大于18秒的记为正数,成绩小于18秒的记为负数,第一小组8名女生的成绩记录如下:
-1,+0.8,0,-1.2,-0.1,0,+0.5,-0.6.
这组女生的达标率为多少?平均成绩为多少秒?
2.已知两组数据:x1、x2、…、xn和y1、y2、…、yn,它们的平均数分别是和.分别求下列各组新数据的平均数:
(1)3x1、3x2、…、3xn;
(2)x1+y1、x2+y2、…、xn+yn.
类型2 中位数和众数
3.(福建宁德)某初中学校组织200位同学参加义务植树活动,每人植树的棵数在5至10之间.甲、乙两位同学分别调查了30位同学的植树情况,并将收集的数据进行了整理,绘制成统计表分别为表1和表2:
表1:甲调查九年级30位同学植树情况统计表(单位:棵)
/
表2:乙调查三个年级各10位同学植树情况统计表(单位:棵)
/
根据以上材料回答下列问题:
(1)表1中30位同学植树情况的中位数是 棵;
(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是 ,正确的数据应该是 .
(3)指出哪位同学所抽取的样本能更好地反陕此次植树活动情况,并用该样本估计本次活动200位同学共植树多少棵.
类型3 平均数、中位数和众数的应用
4.某学习兴趣小组参加一次单元测试,成绩统计情况如下表:
/
(1)该兴趣小组有多少人?
(2)该兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为该兴趣小组下单元测试设定一个新目标,学生达到或超过目标给予奖励,并希望小组三分之一左右的优秀学生得到奖励,请你帮老师从平均数、中位数、众数三个数中选择一个比较恰当的作为目标;如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
类型4 方差的实际应用
5.甲、乙两台编织机同时编织一种毛衣,在5天中,两台编织机每天出的合格品数量如下(单位:件):
甲:10,8,7,7,8;
乙:9,8,7,7,9.
在这5天中,哪台编织机出合格品的波动较小?
6.甲、乙两台机床同时生产一种零件.在10天中,两台机床每天出次品的数量如下表:
甲
1
1
0
2
1
3
2
1
1
0
乙
0
2
2
0
3
1
0
1
3
1
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果来看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
类型5 统计图表在数据分析中的应用
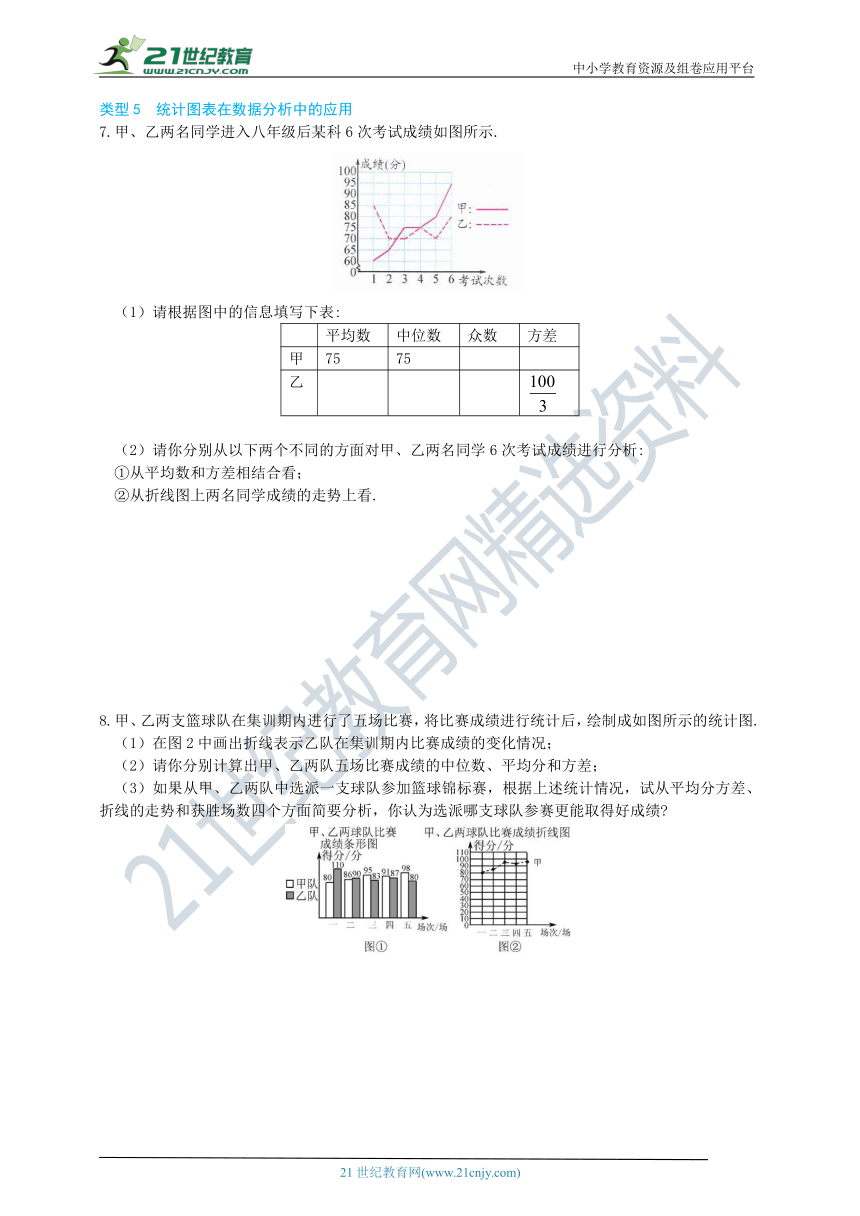
7.甲、乙两名同学进入八年级后某科6次考试成绩如图所示.
/
(1)请根据图中的信息填写下表:
平均数
中位数
众数
方差
甲
75
75
乙
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;
②从折线图上两名同学成绩的走势上看.
8.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图所示的统计图.
(1)在图2中画出折线表示乙队在集训期内比赛成绩的变化情况;
(2)请你分别计算出甲、乙两队五场比赛成绩的中位数、平均分和方差;
(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分方差、折线的走势和获胜场数四个方面简要分析,你认为选派哪支球队参赛更能取得好成绩?
/
参 考 答 案
1.解:由题可知,达标的人数为6,
∴这组女生的达标率=×100%=75%.
平均成绩=18+(-1+0.8+0-1.2-0.1+0+0.5-0.6)÷8=17.8(秒)
2.解:(1)这组数据的平均数为3.
(2)这组数据的平均数为+.
3.解:(1)表1中30位同学植树情况的中位数是9棵,故答案为9;
(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是11,正确的数据应该是12;
(3)乙同学所抽取的样本能更好地反映此次植树活动情况,(3×6+6×7+3×8+12×9+6×10)÷30×200=1680(棵),
答:估计本次活动200位同学一共植树1680棵.
4.(1)该兴趣小组的人数为1+1+5+4+3+2+3+1+1+1+2+3+1+2=30.
(2)本次单元测试成绩的平均数为×(73+74+75×5+76×4+77×3+78×2+79×3+82+83+84+86×2+88×3+90+92×2)=80.3(分);
表格中数据已经按照从小到大的顺序排列,一共有30个数,第15,16个数都是78,所以中位数是78分;
75出现了5次,出现次数最多,所以众数是75分.
(3)由(2)可知,平均数为80.3分,中位数为78分,众数为75分,如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数.
如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为分数在中位数以上的人数占总人数的一半左右.
5.解:甲=×(10+8+7+7+8)=8,
S2甲=×[(10-8)2+2×(8-8)2+2×(7-8)2]=1.2;
乙=×(9+8+7+7+9)=8,
S2乙=×[2×(9-8)2+(8-8)2+2×(7-8)2]=0.8.
∵S2甲>S2乙,
∴乙编织机出合格品的波动较小.
6.解:(1)甲的平均数是(1+1+0+2+1+3+2+1+1+0)÷10=1.2,
甲的平均数是(0+2+2+0+3+1+0+1+3+1)÷10=1.3.
S2甲=×[5×(1-1.2)2+2×(0-1.2)2+2×(2-1.2)2+(3-1.2)2]=0.76,
S2乙=×[3×(0-1.3)2+2×(2-1.3)2+2×(3-1.3)2+3×(1-1.3)2]=1.21.
(2)∵甲=1.2,乙=1.3,甲<乙,
∴甲机床出次品的平均数较小.
∵S2甲=0.76,S2乙=1.21,S2甲∴甲机床出次品的波动较小.
7.解:(1)如下表:
/
(2)①从平均数和方差相结合看,甲、乙两名同学的整体水平相当,平均成绩一样好,但乙同学的成绩更稳定.
②从折线图上两名同学成绩的走势上看,甲同学进步较快,乙同学成绩稳定且有小幅度下滑.
8.解:(1)如图所示:
/
(2)甲队比赛成绩的中位数为91分,乙队比赛成绩的中位数为87分.
甲=×(80+86+95+91+98)=90(分);
乙=×(110+90+83+87+80)=90(分).
S2甲=×[(80-90)2+(86-90)2+(95-90)2+(91-90)2+(98-90)2]=41.2;
S2乙=×[(110-90)2+(90-90)2+(83-90)2+(87-90)2+(80-90)2]=111.6.
(3)从平均分看,两队相等,实力大体相当;从方差来看,S2甲/
本章重点巩固训练
类型1 平均数
1.体育课上全班女生进行百米测试,达标成绩为18秒,现以达标成绩为标准,成绩大于18秒的记为正数,成绩小于18秒的记为负数,第一小组8名女生的成绩记录如下:
-1,+0.8,0,-1.2,-0.1,0,+0.5,-0.6.
这组女生的达标率为多少?平均成绩为多少秒?
2.已知两组数据:x1、x2、…、xn和y1、y2、…、yn,它们的平均数分别是和.分别求下列各组新数据的平均数:
(1)3x1、3x2、…、3xn;
(2)x1+y1、x2+y2、…、xn+yn.
类型2 中位数和众数
3.(福建宁德)某初中学校组织200位同学参加义务植树活动,每人植树的棵数在5至10之间.甲、乙两位同学分别调查了30位同学的植树情况,并将收集的数据进行了整理,绘制成统计表分别为表1和表2:
表1:甲调查九年级30位同学植树情况统计表(单位:棵)
/
表2:乙调查三个年级各10位同学植树情况统计表(单位:棵)
/
根据以上材料回答下列问题:
(1)表1中30位同学植树情况的中位数是 棵;
(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是 ,正确的数据应该是 .
(3)指出哪位同学所抽取的样本能更好地反陕此次植树活动情况,并用该样本估计本次活动200位同学共植树多少棵.
类型3 平均数、中位数和众数的应用
4.某学习兴趣小组参加一次单元测试,成绩统计情况如下表:
/
(1)该兴趣小组有多少人?
(2)该兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为该兴趣小组下单元测试设定一个新目标,学生达到或超过目标给予奖励,并希望小组三分之一左右的优秀学生得到奖励,请你帮老师从平均数、中位数、众数三个数中选择一个比较恰当的作为目标;如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
类型4 方差的实际应用
5.甲、乙两台编织机同时编织一种毛衣,在5天中,两台编织机每天出的合格品数量如下(单位:件):
甲:10,8,7,7,8;
乙:9,8,7,7,9.
在这5天中,哪台编织机出合格品的波动较小?
6.甲、乙两台机床同时生产一种零件.在10天中,两台机床每天出次品的数量如下表:
甲
1
1
0
2
1
3
2
1
1
0
乙
0
2
2
0
3
1
0
1
3
1
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果来看,在10天中,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
类型5 统计图表在数据分析中的应用
7.甲、乙两名同学进入八年级后某科6次考试成绩如图所示.
/
(1)请根据图中的信息填写下表:
平均数
中位数
众数
方差
甲
75
75
乙
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析:
①从平均数和方差相结合看;
②从折线图上两名同学成绩的走势上看.
8.甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图所示的统计图.
(1)在图2中画出折线表示乙队在集训期内比赛成绩的变化情况;
(2)请你分别计算出甲、乙两队五场比赛成绩的中位数、平均分和方差;
(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分方差、折线的走势和获胜场数四个方面简要分析,你认为选派哪支球队参赛更能取得好成绩?
/
参 考 答 案
1.解:由题可知,达标的人数为6,
∴这组女生的达标率=×100%=75%.
平均成绩=18+(-1+0.8+0-1.2-0.1+0+0.5-0.6)÷8=17.8(秒)
2.解:(1)这组数据的平均数为3.
(2)这组数据的平均数为+.
3.解:(1)表1中30位同学植树情况的中位数是9棵,故答案为9;
(2)已知表2的最后两列中有一个错误的数据,这个错误的数据是11,正确的数据应该是12;
(3)乙同学所抽取的样本能更好地反映此次植树活动情况,(3×6+6×7+3×8+12×9+6×10)÷30×200=1680(棵),
答:估计本次活动200位同学一共植树1680棵.
4.(1)该兴趣小组的人数为1+1+5+4+3+2+3+1+1+1+2+3+1+2=30.
(2)本次单元测试成绩的平均数为×(73+74+75×5+76×4+77×3+78×2+79×3+82+83+84+86×2+88×3+90+92×2)=80.3(分);
表格中数据已经按照从小到大的顺序排列,一共有30个数,第15,16个数都是78,所以中位数是78分;
75出现了5次,出现次数最多,所以众数是75分.
(3)由(2)可知,平均数为80.3分,中位数为78分,众数为75分,如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数.
如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为分数在中位数以上的人数占总人数的一半左右.
5.解:甲=×(10+8+7+7+8)=8,
S2甲=×[(10-8)2+2×(8-8)2+2×(7-8)2]=1.2;
乙=×(9+8+7+7+9)=8,
S2乙=×[2×(9-8)2+(8-8)2+2×(7-8)2]=0.8.
∵S2甲>S2乙,
∴乙编织机出合格品的波动较小.
6.解:(1)甲的平均数是(1+1+0+2+1+3+2+1+1+0)÷10=1.2,
甲的平均数是(0+2+2+0+3+1+0+1+3+1)÷10=1.3.
S2甲=×[5×(1-1.2)2+2×(0-1.2)2+2×(2-1.2)2+(3-1.2)2]=0.76,
S2乙=×[3×(0-1.3)2+2×(2-1.3)2+2×(3-1.3)2+3×(1-1.3)2]=1.21.
(2)∵甲=1.2,乙=1.3,甲<乙,
∴甲机床出次品的平均数较小.
∵S2甲=0.76,S2乙=1.21,S2甲
7.解:(1)如下表:
/
(2)①从平均数和方差相结合看,甲、乙两名同学的整体水平相当,平均成绩一样好,但乙同学的成绩更稳定.
②从折线图上两名同学成绩的走势上看,甲同学进步较快,乙同学成绩稳定且有小幅度下滑.
8.解:(1)如图所示:
/
(2)甲队比赛成绩的中位数为91分,乙队比赛成绩的中位数为87分.
甲=×(80+86+95+91+98)=90(分);
乙=×(110+90+83+87+80)=90(分).
S2甲=×[(80-90)2+(86-90)2+(95-90)2+(91-90)2+(98-90)2]=41.2;
S2乙=×[(110-90)2+(90-90)2+(83-90)2+(87-90)2+(80-90)2]=111.6.
(3)从平均分看,两队相等,实力大体相当;从方差来看,S2甲
