【好题必练】20.3 数据的离散程度同步练习题(含答案)
文档属性
| 名称 | 【好题必练】20.3 数据的离散程度同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 23:07:14 | ||
图片预览


文档简介
第20章 数据的整理与初步处理
20.3 数据的离散程度
/
知识点1 极差
【核心提示1】一组数据中的最大数据与最小数据的差叫做这组数据的 ,即
=最大值-最小值,极差反映了这组数据的 .
1.下列几个常见统计量中能够反映一组数据波动范围的是( )
A.平均数 B.中位数 C.众数 D.极差
2.一组数据为9.9、10.3、10.3、9.9、10.1,则这组数据的极差是( )
A.0.4 B.16 C.0.2 D.无法确定
3.一组数据-1,0,3,5,x的极差是7,那么x的值可能有( )
A.1个 B.2个 C.4个 D.6个
4.一组数据x1、x2…xn的极差是8,则另一组数据2x1+1、2x2+1…,2xn+1的极差是( )
A. 8 B.16 C.9 D.17
5.在某次体育测试中,某班参加仰卧起坐测试的一组女生(每组7人)测试成绩如下:44,45,42,48,46,47,45,则这组数据的极差是 .
6.某空调专卖店十位销售人员七月份的销售数量分别是:7,18,6,31,17,5,11,10,16,21,则其极差是 .
7.已知一组数据2.1、1.9、1.8、x、2.2的平均数为2,则极差是 .
8.一组数据3、-1、0、2、x的极差是5,且x为自然数,则x= .
知识点2 方差
【核心提示2】设有n个数据x1、x2、x3、…xn,各数据与它们的平均数的差的平方分别是(x1-)2、(x2-)2、(x3-)2、…(xn-)2,用这些平方的平均数来衡量这组数据的波动大小,并把它叫做这组数据的 .用公式表示为:S2= .
9.数据1、5、6、5、6、5、6、6的众数是 ,方差是 .
10.(黑龙江绥化)在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .
11.(湖南长沙)甲、乙两名同学进行跳高测试,每人10次跳高的平均成绩恰好都是1.6米,方差分别是s甲2=1.2,s乙2=0.5,则在本次测试中, 同学的成绩更稳定.(填“甲”或“乙”)
12.在某中学举行的演讲比赛中,七年级5名参赛选手的成绩如下表所示,根据表中提供的数据,可得这5名选手成绩的方差是( )
/
A.2 B6.8 C.34 D.93
13.一组数据6,4,a,3,2的平均数是5,则这组数据的方差为( )
A.8 B.5 C.2 D.3
知识点3 用计算器求方差
【核心提示3】用计算器求方差的步骤:(1) ,打开计算器;(2)菜单21,启动“ ”计算功能;(3)输入所有数据;(4)OPTN2,即可获得这组数据的 .其中所对应的数值即为 .
14.某校八年级数学测试中,为了了解甲、乙两班学生的测试成绩情况,从每班抽取10名学生的成绩进行分析(单位:分):
甲:86,78,80,86,92,85,85,87,86,88;
乙:78,91,87,82,85,89,81,86,76,87.
请用计算器分别它们的方差,并根据计算结果说明哪个班的测试成绩比较稳定.
/
15.若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 .
16.若样本1,2,3,x的平均数为5,又样本1,2,3,x,y的平均数为6,则样本1,2,3,x,y的极差是 .
17.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则在下列结论①方差是8,②极差是9,③众数是-1,④平均数是-1中,正确的是 (填序号).
18.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9.2环,方差分别为s甲2=0.56,s乙2=0.60,s丙2=0.50,s丁2=0.45,则成绩最稳定的是 .
19.已知一组数据x1,x2,x3,x4,x5的方差是,那么另一组数据3x-21,3x2-2,3x3-2,3x4-2,3x5-2的方差是 .
20.(安徽铜陵)铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
21.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
/
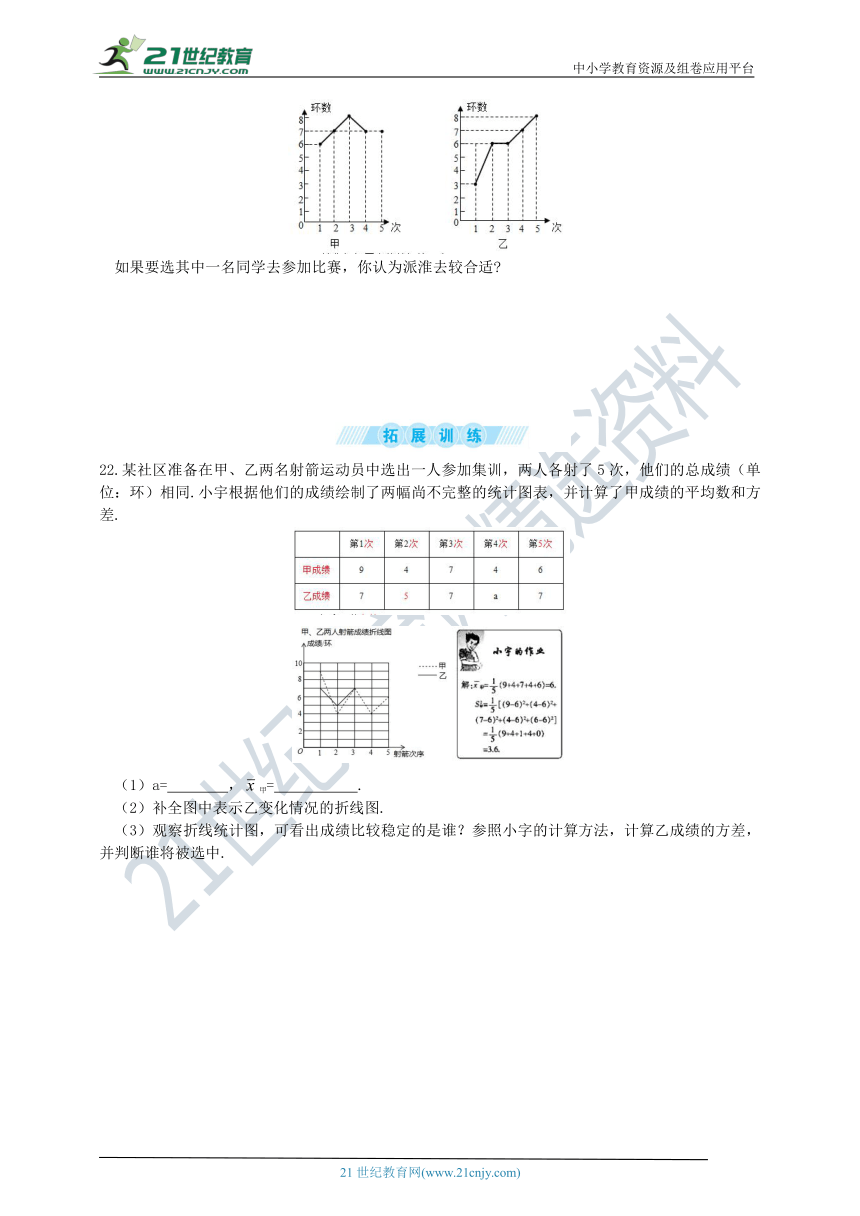
22.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
参 考 答 案
核心提示1 极差 极差 波动范围
1.D
2.A
3.B
4.B
5.6
6.26
7.0.30
8.4或-2
核心提示2 方差 [(x1-)2+(x2-)2+(x3-)2+…+(xn-)2]
9.6 2.5
10.2
11.乙
12.B
13.A
核心提示3 开机 单变量统计 统计值 方差
14.解:(1)开机,打开计算器;
(2)菜单21,启动“ 单变量统计”计算功能;
(3)分别输入甲、乙两班学生成绩;
(4)OPTN2,计算出甲班的测试成绩的方差为13.81,乙班的测试成绩的方差为20.96.
因为甲班的测试成绩的方差小于乙班的测试成绩的方差,所以甲班的测试成绩比较稳定.
15.30,40
16.19
17.②③④
18.丁
19.3
20.解:(1)甲的成绩从小到大排列为78,79,81,82,84,88,93,95,则甲成绩的中位数为=83(分).
乙的平均数为=85(分),
乙成绩的方差为
=41.
(2)选派甲同学参加合适.理由:从平均数上看甲、乙相同,说明甲、乙的实力相当,但是甲的方差比乙小,说明甲的成绩比乙稳定,因此选派甲同学参加合适.
21.解:派甲参赛.
甲=×(6+7+8+7+7)=7(环),
乙=×(3+6+6+7+8)=6(环),
s2甲=×[(6-7)2+(7-7)2+(8-7)2+(7-7)2+(7-7)2]=,
s2乙=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=.
因为甲>乙,且s2甲22.解:(1)4 6
(2)如如所示:
/
(3)乙的成绩比较稳定.
乙=×(7+5+7+4+7)=6(环),
s2乙=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(5-6)2]=1.6.
∵甲=乙,s2乙∴乙的成绩比较稳定,将被选中.
/
20.3 数据的离散程度
/
知识点1 极差
【核心提示1】一组数据中的最大数据与最小数据的差叫做这组数据的 ,即
=最大值-最小值,极差反映了这组数据的 .
1.下列几个常见统计量中能够反映一组数据波动范围的是( )
A.平均数 B.中位数 C.众数 D.极差
2.一组数据为9.9、10.3、10.3、9.9、10.1,则这组数据的极差是( )
A.0.4 B.16 C.0.2 D.无法确定
3.一组数据-1,0,3,5,x的极差是7,那么x的值可能有( )
A.1个 B.2个 C.4个 D.6个
4.一组数据x1、x2…xn的极差是8,则另一组数据2x1+1、2x2+1…,2xn+1的极差是( )
A. 8 B.16 C.9 D.17
5.在某次体育测试中,某班参加仰卧起坐测试的一组女生(每组7人)测试成绩如下:44,45,42,48,46,47,45,则这组数据的极差是 .
6.某空调专卖店十位销售人员七月份的销售数量分别是:7,18,6,31,17,5,11,10,16,21,则其极差是 .
7.已知一组数据2.1、1.9、1.8、x、2.2的平均数为2,则极差是 .
8.一组数据3、-1、0、2、x的极差是5,且x为自然数,则x= .
知识点2 方差
【核心提示2】设有n个数据x1、x2、x3、…xn,各数据与它们的平均数的差的平方分别是(x1-)2、(x2-)2、(x3-)2、…(xn-)2,用这些平方的平均数来衡量这组数据的波动大小,并把它叫做这组数据的 .用公式表示为:S2= .
9.数据1、5、6、5、6、5、6、6的众数是 ,方差是 .
10.(黑龙江绥化)在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .
11.(湖南长沙)甲、乙两名同学进行跳高测试,每人10次跳高的平均成绩恰好都是1.6米,方差分别是s甲2=1.2,s乙2=0.5,则在本次测试中, 同学的成绩更稳定.(填“甲”或“乙”)
12.在某中学举行的演讲比赛中,七年级5名参赛选手的成绩如下表所示,根据表中提供的数据,可得这5名选手成绩的方差是( )
/
A.2 B6.8 C.34 D.93
13.一组数据6,4,a,3,2的平均数是5,则这组数据的方差为( )
A.8 B.5 C.2 D.3
知识点3 用计算器求方差
【核心提示3】用计算器求方差的步骤:(1) ,打开计算器;(2)菜单21,启动“ ”计算功能;(3)输入所有数据;(4)OPTN2,即可获得这组数据的 .其中所对应的数值即为 .
14.某校八年级数学测试中,为了了解甲、乙两班学生的测试成绩情况,从每班抽取10名学生的成绩进行分析(单位:分):
甲:86,78,80,86,92,85,85,87,86,88;
乙:78,91,87,82,85,89,81,86,76,87.
请用计算器分别它们的方差,并根据计算结果说明哪个班的测试成绩比较稳定.
/
15.若10个数的平均数是3,极差是4,则将这10个数都扩大10倍,则这组数据的平均数是 ,极差是 .
16.若样本1,2,3,x的平均数为5,又样本1,2,3,x,y的平均数为6,则样本1,2,3,x,y的极差是 .
17.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则在下列结论①方差是8,②极差是9,③众数是-1,④平均数是-1中,正确的是 (填序号).
18.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9.2环,方差分别为s甲2=0.56,s乙2=0.60,s丙2=0.50,s丁2=0.45,则成绩最稳定的是 .
19.已知一组数据x1,x2,x3,x4,x5的方差是,那么另一组数据3x-21,3x2-2,3x3-2,3x4-2,3x5-2的方差是 .
20.(安徽铜陵)铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
21.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
/
22.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
参 考 答 案
核心提示1 极差 极差 波动范围
1.D
2.A
3.B
4.B
5.6
6.26
7.0.30
8.4或-2
核心提示2 方差 [(x1-)2+(x2-)2+(x3-)2+…+(xn-)2]
9.6 2.5
10.2
11.乙
12.B
13.A
核心提示3 开机 单变量统计 统计值 方差
14.解:(1)开机,打开计算器;
(2)菜单21,启动“ 单变量统计”计算功能;
(3)分别输入甲、乙两班学生成绩;
(4)OPTN2,计算出甲班的测试成绩的方差为13.81,乙班的测试成绩的方差为20.96.
因为甲班的测试成绩的方差小于乙班的测试成绩的方差,所以甲班的测试成绩比较稳定.
15.30,40
16.19
17.②③④
18.丁
19.3
20.解:(1)甲的成绩从小到大排列为78,79,81,82,84,88,93,95,则甲成绩的中位数为=83(分).
乙的平均数为=85(分),
乙成绩的方差为
=41.
(2)选派甲同学参加合适.理由:从平均数上看甲、乙相同,说明甲、乙的实力相当,但是甲的方差比乙小,说明甲的成绩比乙稳定,因此选派甲同学参加合适.
21.解:派甲参赛.
甲=×(6+7+8+7+7)=7(环),
乙=×(3+6+6+7+8)=6(环),
s2甲=×[(6-7)2+(7-7)2+(8-7)2+(7-7)2+(7-7)2]=,
s2乙=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=.
因为甲>乙,且s2甲
(2)如如所示:
/
(3)乙的成绩比较稳定.
乙=×(7+5+7+4+7)=6(环),
s2乙=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(5-6)2]=1.6.
∵甲=乙,s2乙
/
