【好题必练】第18章 平行四边形单元检测题(含答案)
文档属性
| 名称 | 【好题必练】第18章 平行四边形单元检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 23:14:10 | ||
图片预览



文档简介
第18章检测题
一、选择题(每题3分,共36分)
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数比,其中能判定四边形ABCD是平行四边形的是( )
A.3:2:3:2 B.3:3:5:5 C.1:2:3:4 D.5:4:3:2 2.在□ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
3.平行四边形的两条对角线分别为6和10则其中一条边x的取值范围为( )
A.44.平行四边形的周长为24cm相邻两边长的比为3:1,那么这个平行四边形较短的边长为( )
A.6cm B.3cm C.9cm D.12cm
5.在下列给定的条件中,能画出平行四边形的是( )
A.以60cm为条对角线,20cm,34cm为两邻边
B.以6cm,10cm为对角线,8cm为一边
C.以6cm为一条对角线,3cm和10cm为两邻边
D.以20cm,36cm为对角线,22cm为边
6.如图,在□ABCD中,下列各式不一定正确的是( )
A∠1+∠2=180° B.∠2+∠3=180°
C.∠3+∠4=180° D.∠2+∠4=180°
7.在等腰△ABC中,∠C=90°,BC=2厘米,如果以AC的中点0为旋转中心,将这个三角形旋转180°,B落在点B’处,那么点B’与点B的原来位置相距多少厘米( )
A. B.2 C. D.2
8.如图,在□ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连接OE,则图中平行四边形的个数为( )
A.1 B.2. C.3 D.4
第8题图 第9题图 第11题图
9.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
A.8 B.6 C.4 D.3
10.四边形ABCD中,对角线AC,BD相交于点0,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.A0=CO,BO=DO D.AB∥DC,AD=BC
11.在四边形ABCD中,对角线AC,BD相交于点0,给出如下四组条件: ①0A=0C,0B=0D;②AB=CD,AD=BC;③AB∥CD,AB=CD;④AD=BC,AB∥CD.
其中能判定四边形ABCD是平行四边形的共有( )
A.1组 B.2组 C.3组 D.4组
12.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2? ? B.4 ?C.4? ?D.8 二、填空题(每空4分,共24分)
13.在□ABCD中∠A+∠C=200°,则∠B= .
14.如图,在△ABC中,AB=AC,作△ABC关于点O的中心对称图形△FEC,若△ABC的面积为3,则四边形ABFE的面积为 .
第14题图 第15题图 第16题图 第17题图 第18题图
15.如图,BC为固定的木条,AB,AC为可伸缩的橡皮筋,当点A在与BC平行的轨道上滑动时,△ABC的面积将如何变化 .(变大、变小、不变、不一定)
16.如图,在□ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=50°,则∠D= .
17.如图,在□ABCD中,∠A=70°,将ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF的大小为 .
18.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点若AC+BD=24cm,△OAB的周长是18cm,则EF= cm.
三、解答题.(共90分)
19.(8分)如图,在△ABC中,∠ACB=90°,D是BC边的中点,DE⊥BC,CE∥AD.若AC=2,CE=4,求四边形ACEB的周长.
20.(10分)如图,四边形ABCD是平行四边形,AB=10,AD=8,DB⊥AD. (1)求OB,AC的长; (2)求平行四边形ABCD的面积.
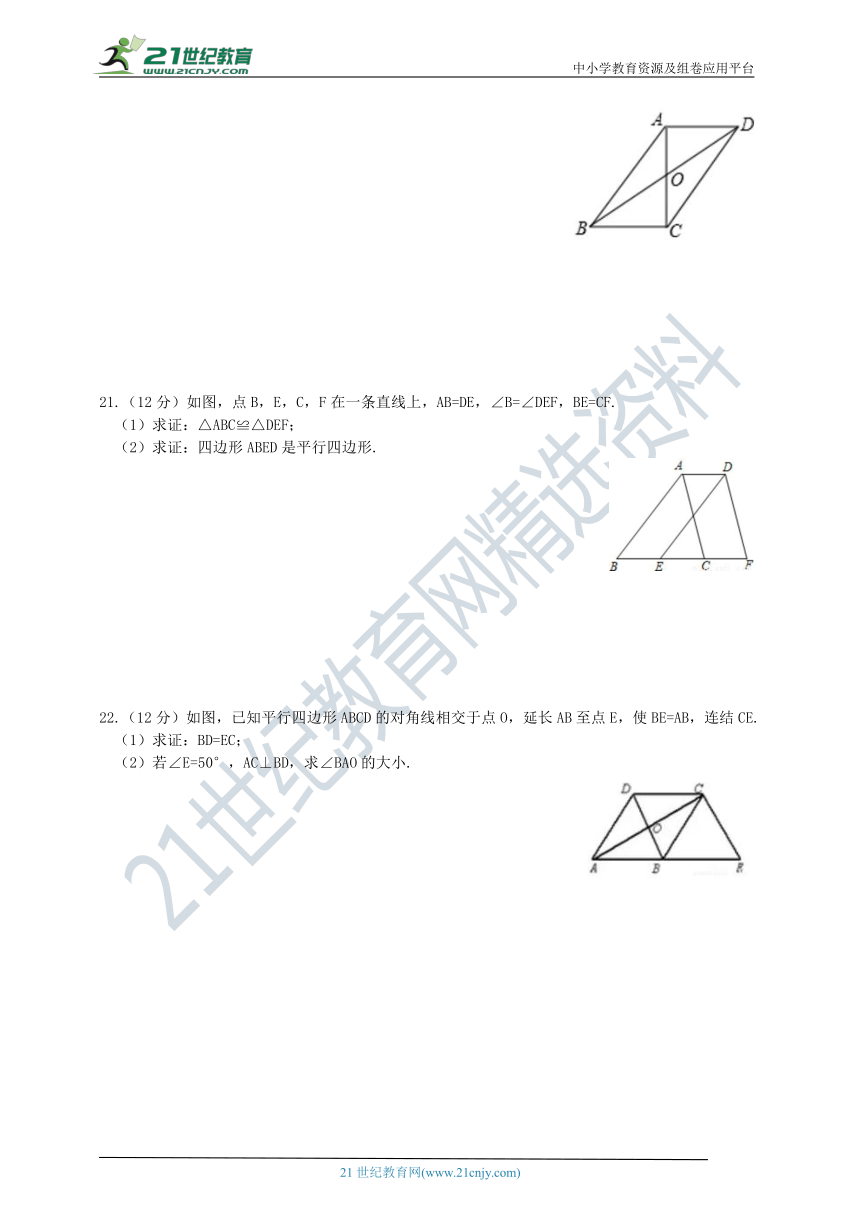
21.(12分)如图,点B,E,C,F在一条直线上,AB=DE,∠B=∠DEF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ABED是平行四边形.
22.(12分)如图,已知平行四边形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50°,AC⊥BD,求∠BAO的大小.
23.(14分)如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=MN.
24.(16分)如图,在□ABCD中,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数; (2)如果AD=5cm,AP=8cm,求△APB的周长.
25.(18分)(黑龙江大庆)如图,等腰△ABC以BC为底边,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BF=BE.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.
参 考 答 案
一、1.A 2.B 3.B 4.B 5.D 6.D 7.D 8.D 9.C 10.D 11.C 12.B
二、13.80° 14.12 15.不变 16.80 17.40° 18.3
三、19.解:∵∠ACB=90°,DE⊥BC,
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形,
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD==2.
∵D是BC边的中点,
∴BC=2CD=4.
在Rt△ABC中,由勾股定理得AB==2.
∵D是BC边的中点,DE⊥BC,
∴EB=EC=4,
∴四边形ACEB的周长=AC+CE+EB+BA=10+2.
20.解:(1)∵四边形ABCD是平行四边形, ∴OA=0C,OB=OD. ∵BD⊥AD,∴在Rt△ABD中,
由勾股定理,得DB==6,
∴OB=OD=DB=×6=3. 在Rt△ADO中,由勾股定理,得 OA=,
∴AC=2. (2)S□ABCD=AD·DB=8×6=48.
21.证明:(1)∵BE=CF, ∴BE+EC=CF+EC,即BC=EF.
又∵∠B=∠DEF,AB=DE,
∴△ABC≌△DEF.
(2)∵∠B=∠DEF,
∴AB∥DE
又∵AB=DE,
∴四边形ABED是平行四边形.
22.(1)证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD.
又∵BE=AB,E在AB的延长线上,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∴BD=EC.
(2)解:∵四边形BECD是平行四边形,
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
23.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD,BC的中点.
∴MD=NC,
又∵MD∥NC,
∴四边形MNCD是平行四边形.
(2)连结DN. ∵N是BC的中点,BC=2CD,
∴CD=NC.∴∠C=60°,
∴△DCN是等边三角形,
∴ND=NC,∠DNC=∠NDC=60°,
∴ND=NB=CN,
∴∠DBC=∠BDN=30°,
∴∠BDC=∠BDN+∠NDC=90°,
∴BD=CD.
∴四边形MNCD是平行四边形,
∴MN=CD,
∴BD=MN.
24.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,
∠APB=180°-(∠PAB+∠PBA)=90°.
(2)∵AP平分∠DAB且AB∥CD,
∴∠DAP=∠PAB=∠DPA,
∴△ADP是等楼三角形,
∴AD=DP=5cm.
同理PC=CB=5cm,即AB=DC=DP+PC=10cm.
在Rt△APB中,AB=10cm,AP=8cm,
∴BP==6cm,
∴Rt△APB的周长量6+8+10=24cm.
25.(1)证明:∵△ABC是等腰三角形,BC为底边,
∴∠ABC=∠C,
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,
∴∠DBG=∠C,∵BE=BF,
∴∠F=∠BEF=∠AEG,
∴∠F=∠DEG,
∴BF∥DE,
∴四边形BDEF为平行四边形. (2)解:∵∠C=45°,
∴∠ABC=∠BFE=∠BEF=45°,
∴△BDE、△BEF均是等腰直角三角形,
∴BE2+BF2=BE2+BE2=EF2=BD2,
∴BF=,
作FM⊥BD交DB的延长线于M,连结DF,如图所示,则△BFM是等腰直角三角形,
∴FM2+BM2=FM2+FM2=BF2,
∴FM=BM=1,
∴DM=3,在Rt△DFM中,由勾股定理,得DF=,即D,F两点间的距离为.
一、选择题(每题3分,共36分)
1.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数比,其中能判定四边形ABCD是平行四边形的是( )
A.3:2:3:2 B.3:3:5:5 C.1:2:3:4 D.5:4:3:2 2.在□ABCD中,∠A:∠B:∠C=2:3:2,则∠D=( )
A.36° B.108° C.72° D.60°
3.平行四边形的两条对角线分别为6和10则其中一条边x的取值范围为( )
A.4
A.6cm B.3cm C.9cm D.12cm
5.在下列给定的条件中,能画出平行四边形的是( )
A.以60cm为条对角线,20cm,34cm为两邻边
B.以6cm,10cm为对角线,8cm为一边
C.以6cm为一条对角线,3cm和10cm为两邻边
D.以20cm,36cm为对角线,22cm为边
6.如图,在□ABCD中,下列各式不一定正确的是( )
A∠1+∠2=180° B.∠2+∠3=180°
C.∠3+∠4=180° D.∠2+∠4=180°
7.在等腰△ABC中,∠C=90°,BC=2厘米,如果以AC的中点0为旋转中心,将这个三角形旋转180°,B落在点B’处,那么点B’与点B的原来位置相距多少厘米( )
A. B.2 C. D.2
8.如图,在□ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连接OE,则图中平行四边形的个数为( )
A.1 B.2. C.3 D.4
第8题图 第9题图 第11题图
9.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
A.8 B.6 C.4 D.3
10.四边形ABCD中,对角线AC,BD相交于点0,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.A0=CO,BO=DO D.AB∥DC,AD=BC
11.在四边形ABCD中,对角线AC,BD相交于点0,给出如下四组条件: ①0A=0C,0B=0D;②AB=CD,AD=BC;③AB∥CD,AB=CD;④AD=BC,AB∥CD.
其中能判定四边形ABCD是平行四边形的共有( )
A.1组 B.2组 C.3组 D.4组
12.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2? ? B.4 ?C.4? ?D.8 二、填空题(每空4分,共24分)
13.在□ABCD中∠A+∠C=200°,则∠B= .
14.如图,在△ABC中,AB=AC,作△ABC关于点O的中心对称图形△FEC,若△ABC的面积为3,则四边形ABFE的面积为 .
第14题图 第15题图 第16题图 第17题图 第18题图
15.如图,BC为固定的木条,AB,AC为可伸缩的橡皮筋,当点A在与BC平行的轨道上滑动时,△ABC的面积将如何变化 .(变大、变小、不变、不一定)
16.如图,在□ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=50°,则∠D= .
17.如图,在□ABCD中,∠A=70°,将ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF的大小为 .
18.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点若AC+BD=24cm,△OAB的周长是18cm,则EF= cm.
三、解答题.(共90分)
19.(8分)如图,在△ABC中,∠ACB=90°,D是BC边的中点,DE⊥BC,CE∥AD.若AC=2,CE=4,求四边形ACEB的周长.
20.(10分)如图,四边形ABCD是平行四边形,AB=10,AD=8,DB⊥AD. (1)求OB,AC的长; (2)求平行四边形ABCD的面积.
21.(12分)如图,点B,E,C,F在一条直线上,AB=DE,∠B=∠DEF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ABED是平行四边形.
22.(12分)如图,已知平行四边形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=50°,AC⊥BD,求∠BAO的大小.
23.(14分)如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=MN.
24.(16分)如图,在□ABCD中,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数; (2)如果AD=5cm,AP=8cm,求△APB的周长.
25.(18分)(黑龙江大庆)如图,等腰△ABC以BC为底边,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BF=BE.
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.
参 考 答 案
一、1.A 2.B 3.B 4.B 5.D 6.D 7.D 8.D 9.C 10.D 11.C 12.B
二、13.80° 14.12 15.不变 16.80 17.40° 18.3
三、19.解:∵∠ACB=90°,DE⊥BC,
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形,
∴DE=AC=2.
在Rt△CDE中,由勾股定理得CD==2.
∵D是BC边的中点,
∴BC=2CD=4.
在Rt△ABC中,由勾股定理得AB==2.
∵D是BC边的中点,DE⊥BC,
∴EB=EC=4,
∴四边形ACEB的周长=AC+CE+EB+BA=10+2.
20.解:(1)∵四边形ABCD是平行四边形, ∴OA=0C,OB=OD. ∵BD⊥AD,∴在Rt△ABD中,
由勾股定理,得DB==6,
∴OB=OD=DB=×6=3. 在Rt△ADO中,由勾股定理,得 OA=,
∴AC=2. (2)S□ABCD=AD·DB=8×6=48.
21.证明:(1)∵BE=CF, ∴BE+EC=CF+EC,即BC=EF.
又∵∠B=∠DEF,AB=DE,
∴△ABC≌△DEF.
(2)∵∠B=∠DEF,
∴AB∥DE
又∵AB=DE,
∴四边形ABED是平行四边形.
22.(1)证明:∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD.
又∵BE=AB,E在AB的延长线上,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∴BD=EC.
(2)解:∵四边形BECD是平行四边形,
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
23.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD,BC的中点.
∴MD=NC,
又∵MD∥NC,
∴四边形MNCD是平行四边形.
(2)连结DN. ∵N是BC的中点,BC=2CD,
∴CD=NC.∴∠C=60°,
∴△DCN是等边三角形,
∴ND=NC,∠DNC=∠NDC=60°,
∴ND=NB=CN,
∴∠DBC=∠BDN=30°,
∴∠BDC=∠BDN+∠NDC=90°,
∴BD=CD.
∴四边形MNCD是平行四边形,
∴MN=CD,
∴BD=MN.
24.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,
∠APB=180°-(∠PAB+∠PBA)=90°.
(2)∵AP平分∠DAB且AB∥CD,
∴∠DAP=∠PAB=∠DPA,
∴△ADP是等楼三角形,
∴AD=DP=5cm.
同理PC=CB=5cm,即AB=DC=DP+PC=10cm.
在Rt△APB中,AB=10cm,AP=8cm,
∴BP==6cm,
∴Rt△APB的周长量6+8+10=24cm.
25.(1)证明:∵△ABC是等腰三角形,BC为底边,
∴∠ABC=∠C,
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,
∴∠DBG=∠C,∵BE=BF,
∴∠F=∠BEF=∠AEG,
∴∠F=∠DEG,
∴BF∥DE,
∴四边形BDEF为平行四边形. (2)解:∵∠C=45°,
∴∠ABC=∠BFE=∠BEF=45°,
∴△BDE、△BEF均是等腰直角三角形,
∴BE2+BF2=BE2+BE2=EF2=BD2,
∴BF=,
作FM⊥BD交DB的延长线于M,连结DF,如图所示,则△BFM是等腰直角三角形,
∴FM2+BM2=FM2+FM2=BF2,
∴FM=BM=1,
∴DM=3,在Rt△DFM中,由勾股定理,得DF=,即D,F两点间的距离为.
