【好题必练】第19章 矩形、菱形与正方形单元检测题(含答案)
文档属性
| 名称 | 【好题必练】第19章 矩形、菱形与正方形单元检测题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览

文档简介
第19章检测题
一、选择题(每题3分,共36分)
1.下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是菱形
D.对角线垂直且相等的四边形是正方形
2.不能判断四边形ABCD是矩形的是(O为对角线的交点)( )
A.AB=CD,AD=BC,∠A=90° B.OA=OB=0C=OD
C.AB⊥CD.AC=BD D.AB⊥CD,OA-OC,OB=OD
3.能判定四边形ABCD是菱形的条件是( )
A.对角线AC平分对角线BD,且AC⊥BD
B.对角线AC平分对角线BD,且∠A=∠C
C.对角线AC平分对角线BD,且平分∠A和∠C
D.对角线AC平分∠A和∠C,且∠A=∠C
4.在下列性质中:①对角线互相平分;②对边相等;③对角线互相垂直且相等;④对角相等.矩形和菱形都具有的性质是( )
A.①②③? ?B.①②④?? C.①③? ?D.③④
5.四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则在下列推理不成立的是( )
A.①④→⑥? B.①③→⑤?? C.①②→⑥? ?D.②③→④
6.已知四边形ABCD是平行四边形,两条对角线AC、BD交于点O,则其中全等的三角形有( )
A.2对 B.3对 C.4对 D.5对
7.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是( )
A.4 B.6 C.8 D.10
第7题图 第8题图 第9题图
8.如图,将张矩形的纸片折叠,则折叠后所得的∠FED的度数是( )
A.60° B.120? C.90° D.无法判断
9.如图,点0是矩形ABCD的对角线AC的中点,0M∥AB交AD于点M,若0M=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
10.已知点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
11.如图,在△ABC中点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.则下列条件中,能使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC
C.AB=AC D.BF∥CE
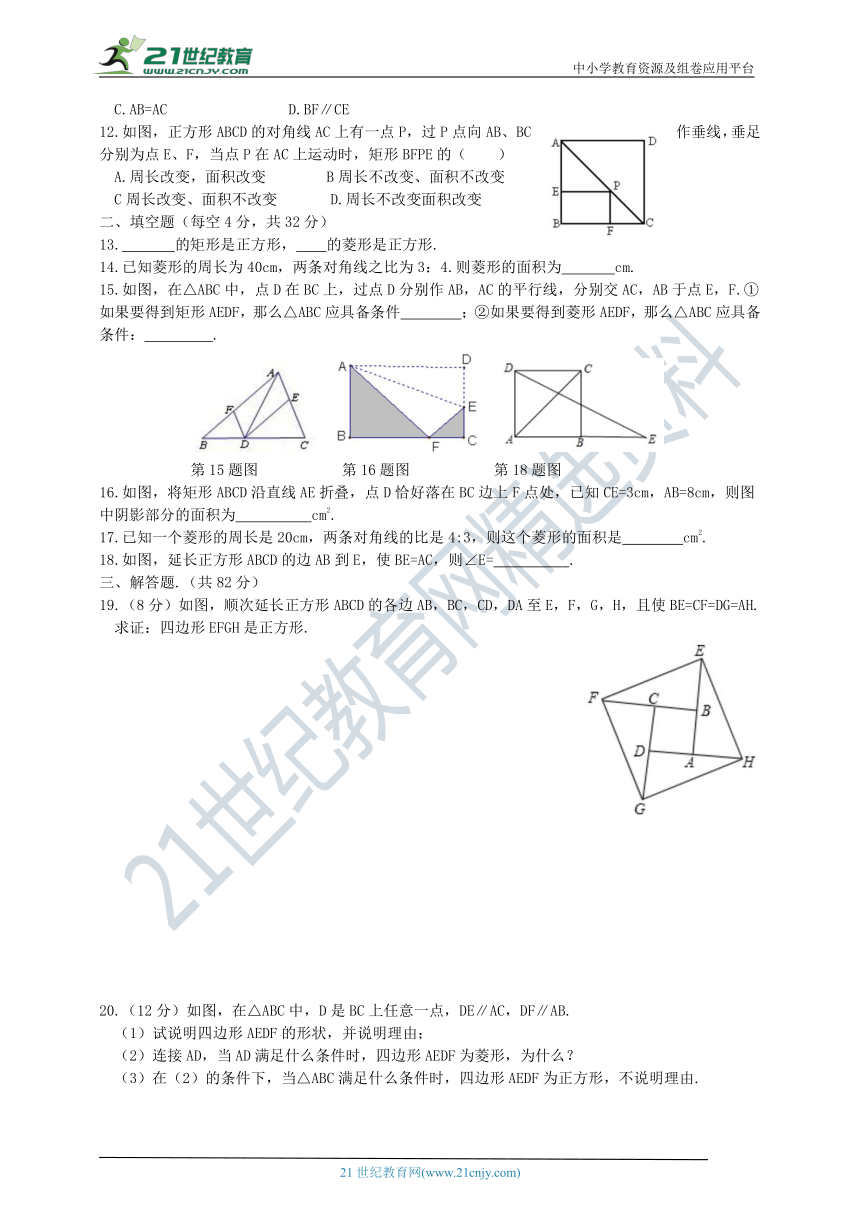
12.如图,正方形ABCD的对角线AC上有一点P,过P点向AB、BC作垂线,垂足分别为点E、F,当点P在AC上运动时,矩形BFPE的( )
A.周长改变,面积改变 B周长不改变、面积不改变
C周长改变、面积不改变 D.周长不改变面积改变
二、填空题(每空4分,共32分)
13. 的矩形是正方形,??的菱形是正方形. 14.已知菱形的周长为40cm,两条对角线之比为3:4.则菱形的面积为 cm. 15.如图,在△ABC中,点D在BC上,过点D分别作AB,AC的平行线,分别交AC,AB于点E,F.①如果要得到矩形AEDF,那么△ABC应具备条件 ;②如果要得到菱形AEDF,那么△ABC应具备条件: .
第15题图 第16题图 第18题图
16.如图,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,则图中阴影部分的面积为 cm2.
17.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是 cm2.
18.如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E= .
三、解答题.(共82分)
19.(8分)如图,顺次延长正方形ABCD的各边AB,BC,CD,DA至E,F,G,H,且使BE=CF=DG=AH.求证:四边形EFGH是正方形.
20.(12分)如图,在△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由; (2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么? (3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
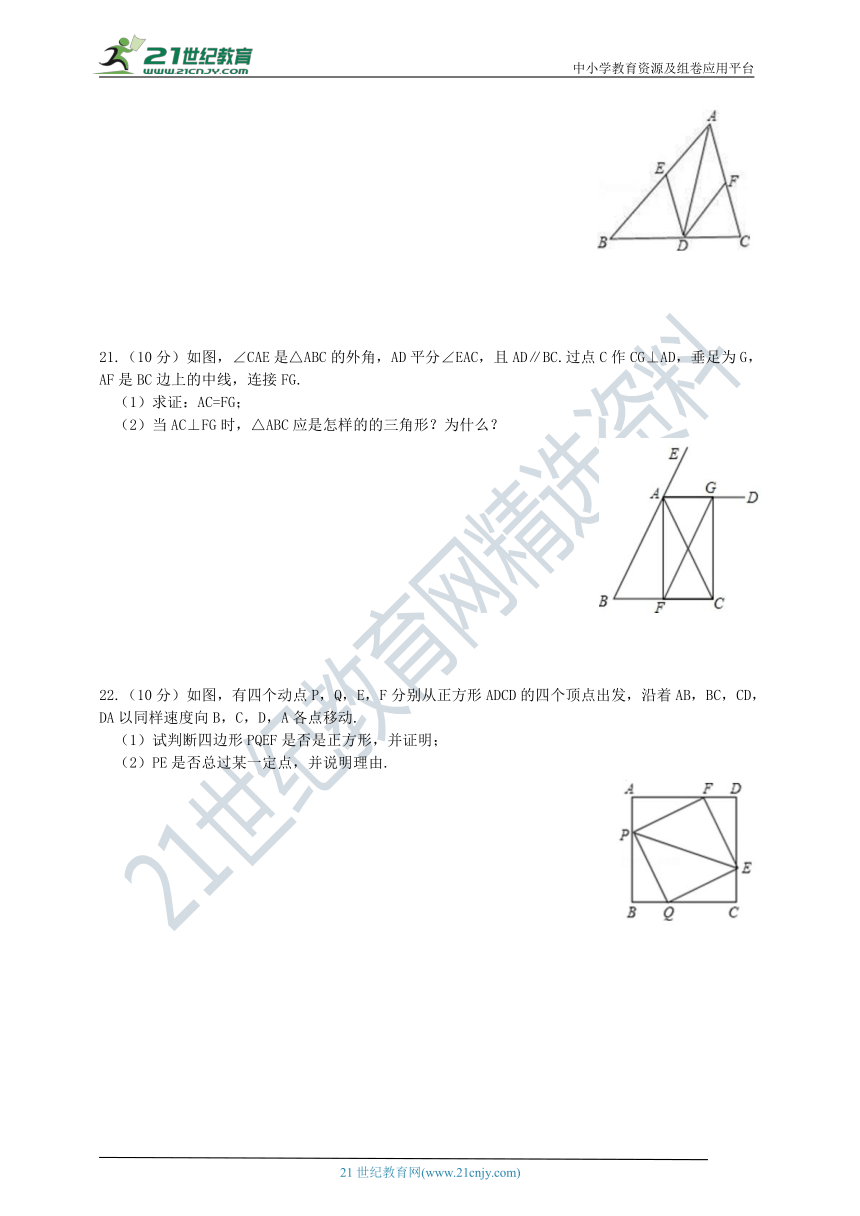
21.(10分)如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG; (2)当AC⊥FG时,△ABC应是怎样的的三角形?为什么?
22.(10分)如图,有四个动点P,Q,E,F分别从正方形ADCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
(1)试判断四边形PQEF是否是正方形,并证明; (2)PE是否总过某一定点,并说明理由.
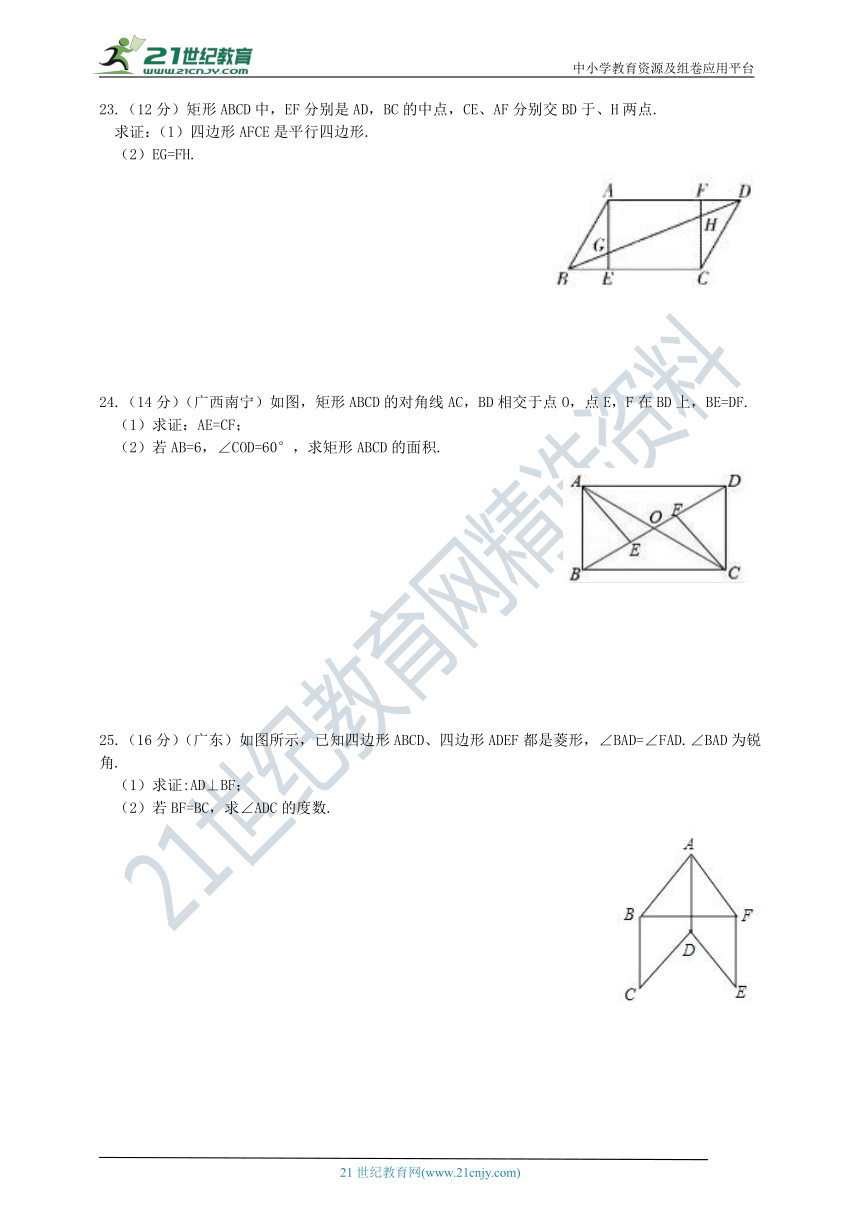
23.(12分)矩形ABCD中,EF分别是AD,BC的中点,CE、AF分别交BD于、H两点.
求证:(1)四边形AFCE是平行四边形.
(2)EG=FH.
24.(14分)(广西南宁)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
25.(16分)(广东)如图所示,已知四边形ABCD、四边形ADEF都是菱形,∠BAD=∠FAD.∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
参 考 答 案
一、1.B 2.D 3.D 4.B 5.C 6.D 7.C 8.C 9.D 10.C 11.C 12.D
二、13.有一组邻边相等 有一个角为直角 14.96 15.∠BAC=90° AD平分∠BAC 16.30 17.24 18.22.5°
三、19.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠EBF=∠HAE=∠GDH=∠FOG,
又∵BE=CF=DG=AH,
∴CG=DH=AE=BF,
∴△AEH≌△CGF≌△DHG≌△BFE,
∴EF=FG=GH=HE,∠EFB=∠HEA,
∴四边形EFGH为菱形,
∵∠EFB+∠FEB=90°,
∴∠FEB+∠HEA=90°,
∴四边形EFGH是正方形.
20.解:(1):∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
∴当AD平分∠BAC时,四边形AEDF为菱形,
(3)由四边形AEDF为正方形,
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
21.解:(1)∵AD平分∠EAC,且AD∥BC,
∴∠ABC=∠EAD=∠CAD=∠ACB,
∴AB=AC.
∵AF是BC边上的中线,
∴AF⊥BC,
∵CG⊥AD,AD∥BC,
∴CG⊥BC,
∴AF∥CG,
∴四边形AFCG是平行四边形,
∵∠AFC=90?,
∴四边形AFCG是矩形,
∴AC=FG.
(2)当AC⊥FG时,△ABC是等腰直角三角形.
理由如下:∵四边形AFCG是矩形,
∴四边形AFCG是正方形,∠ACB=45°,
∵AB=AC,
∴△ABC是等腰直角三角形.
22.解:(1)在正方形ABCD中,
AP=BQ=CE=DF,AB=BC=CD=DA,
∴BP=QC=ED=FA.
又∵∠A=∠B=∠C=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF,
∴FP=PQ=QE=EF,∠APF=∠PQB
∴四边形PQEF是菱形,∠APF+∠BPQ=90°,
∴∠FPQ= 90°,∴四边形PQEF为正方形.
(2)连接AC交PE于O,连接AE,PC,如下图,
∵AP平行且等于EC,
∴四边形APCE为平行四边形.
∵O为对角线AC的中点,
∴对角线PE总过AC的中点.
23.证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是ADBC的中点
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵∴AD∥BC,
∴∠EDG=∠FBH.
在△DEG和△BFH中,
,
∴△DEG≌△BFH(AAS)
∴EG=FH.
24.(1)证明:∵四边形ABCD是矩形.
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,
∴0E=OF.
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=∠C0D=60°,
∴△AOB是等边三角形,
∴0A=AB=6,
∴AC=20A=12.
在Rt△ABC中,BC==6,
∴矩形ABCD的面积=AB·BC=6×6=36.
25.(1)证明:如图,连结DB、DF.
∵四边形ABCD、四边形ADEF都是菱形,
∴AB=BC=CD=DA,AD=DE=EF=FA,
在△BAD与△FAD中,
,
∴△BAD≌△FAD,
∴DB=DF,
∴D在线段BF的垂直平分线上,
∵AB=AF,
∴A在线段BF的垂直平分线上,
∴AD是线段BF的垂直平分线,
∴AD⊥BF.
(2)解:如图,设AD⊥BF于H,作DG⊥BC于G,则四边形BCDH是矩形.
∴DG=BH=BF.
∵BF=BC,BC=CD,
∴DG=CD.
在直角△CDG中,
∵∠0CD=90°,DG=CD,
∴∠C=30°,
∵BC∥AD,
∴∠ADC=180°-∠C=150°.
一、选择题(每题3分,共36分)
1.下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是菱形
D.对角线垂直且相等的四边形是正方形
2.不能判断四边形ABCD是矩形的是(O为对角线的交点)( )
A.AB=CD,AD=BC,∠A=90° B.OA=OB=0C=OD
C.AB⊥CD.AC=BD D.AB⊥CD,OA-OC,OB=OD
3.能判定四边形ABCD是菱形的条件是( )
A.对角线AC平分对角线BD,且AC⊥BD
B.对角线AC平分对角线BD,且∠A=∠C
C.对角线AC平分对角线BD,且平分∠A和∠C
D.对角线AC平分∠A和∠C,且∠A=∠C
4.在下列性质中:①对角线互相平分;②对边相等;③对角线互相垂直且相等;④对角相等.矩形和菱形都具有的性质是( )
A.①②③? ?B.①②④?? C.①③? ?D.③④
5.四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD,则在下列推理不成立的是( )
A.①④→⑥? B.①③→⑤?? C.①②→⑥? ?D.②③→④
6.已知四边形ABCD是平行四边形,两条对角线AC、BD交于点O,则其中全等的三角形有( )
A.2对 B.3对 C.4对 D.5对
7.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是( )
A.4 B.6 C.8 D.10
第7题图 第8题图 第9题图
8.如图,将张矩形的纸片折叠,则折叠后所得的∠FED的度数是( )
A.60° B.120? C.90° D.无法判断
9.如图,点0是矩形ABCD的对角线AC的中点,0M∥AB交AD于点M,若0M=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
10.已知点A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
11.如图,在△ABC中点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.则下列条件中,能使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC
C.AB=AC D.BF∥CE
12.如图,正方形ABCD的对角线AC上有一点P,过P点向AB、BC作垂线,垂足分别为点E、F,当点P在AC上运动时,矩形BFPE的( )
A.周长改变,面积改变 B周长不改变、面积不改变
C周长改变、面积不改变 D.周长不改变面积改变
二、填空题(每空4分,共32分)
13. 的矩形是正方形,??的菱形是正方形. 14.已知菱形的周长为40cm,两条对角线之比为3:4.则菱形的面积为 cm. 15.如图,在△ABC中,点D在BC上,过点D分别作AB,AC的平行线,分别交AC,AB于点E,F.①如果要得到矩形AEDF,那么△ABC应具备条件 ;②如果要得到菱形AEDF,那么△ABC应具备条件: .
第15题图 第16题图 第18题图
16.如图,将矩形ABCD沿直线AE折叠,点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,则图中阴影部分的面积为 cm2.
17.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是 cm2.
18.如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E= .
三、解答题.(共82分)
19.(8分)如图,顺次延长正方形ABCD的各边AB,BC,CD,DA至E,F,G,H,且使BE=CF=DG=AH.求证:四边形EFGH是正方形.
20.(12分)如图,在△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由; (2)连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么? (3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
21.(10分)如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
(1)求证:AC=FG; (2)当AC⊥FG时,△ABC应是怎样的的三角形?为什么?
22.(10分)如图,有四个动点P,Q,E,F分别从正方形ADCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.
(1)试判断四边形PQEF是否是正方形,并证明; (2)PE是否总过某一定点,并说明理由.
23.(12分)矩形ABCD中,EF分别是AD,BC的中点,CE、AF分别交BD于、H两点.
求证:(1)四边形AFCE是平行四边形.
(2)EG=FH.
24.(14分)(广西南宁)如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.
25.(16分)(广东)如图所示,已知四边形ABCD、四边形ADEF都是菱形,∠BAD=∠FAD.∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
参 考 答 案
一、1.B 2.D 3.D 4.B 5.C 6.D 7.C 8.C 9.D 10.C 11.C 12.D
二、13.有一组邻边相等 有一个角为直角 14.96 15.∠BAC=90° AD平分∠BAC 16.30 17.24 18.22.5°
三、19.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠EBF=∠HAE=∠GDH=∠FOG,
又∵BE=CF=DG=AH,
∴CG=DH=AE=BF,
∴△AEH≌△CGF≌△DHG≌△BFE,
∴EF=FG=GH=HE,∠EFB=∠HEA,
∴四边形EFGH为菱形,
∵∠EFB+∠FEB=90°,
∴∠FEB+∠HEA=90°,
∴四边形EFGH是正方形.
20.解:(1):∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
(2)∵四边形AEDF为菱形,
∴AD平分∠BAC,
∴当AD平分∠BAC时,四边形AEDF为菱形,
(3)由四边形AEDF为正方形,
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
21.解:(1)∵AD平分∠EAC,且AD∥BC,
∴∠ABC=∠EAD=∠CAD=∠ACB,
∴AB=AC.
∵AF是BC边上的中线,
∴AF⊥BC,
∵CG⊥AD,AD∥BC,
∴CG⊥BC,
∴AF∥CG,
∴四边形AFCG是平行四边形,
∵∠AFC=90?,
∴四边形AFCG是矩形,
∴AC=FG.
(2)当AC⊥FG时,△ABC是等腰直角三角形.
理由如下:∵四边形AFCG是矩形,
∴四边形AFCG是正方形,∠ACB=45°,
∵AB=AC,
∴△ABC是等腰直角三角形.
22.解:(1)在正方形ABCD中,
AP=BQ=CE=DF,AB=BC=CD=DA,
∴BP=QC=ED=FA.
又∵∠A=∠B=∠C=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF,
∴FP=PQ=QE=EF,∠APF=∠PQB
∴四边形PQEF是菱形,∠APF+∠BPQ=90°,
∴∠FPQ= 90°,∴四边形PQEF为正方形.
(2)连接AC交PE于O,连接AE,PC,如下图,
∵AP平行且等于EC,
∴四边形APCE为平行四边形.
∵O为对角线AC的中点,
∴对角线PE总过AC的中点.
23.证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是ADBC的中点
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵∴AD∥BC,
∴∠EDG=∠FBH.
在△DEG和△BFH中,
,
∴△DEG≌△BFH(AAS)
∴EG=FH.
24.(1)证明:∵四边形ABCD是矩形.
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,
∴0E=OF.
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=∠C0D=60°,
∴△AOB是等边三角形,
∴0A=AB=6,
∴AC=20A=12.
在Rt△ABC中,BC==6,
∴矩形ABCD的面积=AB·BC=6×6=36.
25.(1)证明:如图,连结DB、DF.
∵四边形ABCD、四边形ADEF都是菱形,
∴AB=BC=CD=DA,AD=DE=EF=FA,
在△BAD与△FAD中,
,
∴△BAD≌△FAD,
∴DB=DF,
∴D在线段BF的垂直平分线上,
∵AB=AF,
∴A在线段BF的垂直平分线上,
∴AD是线段BF的垂直平分线,
∴AD⊥BF.
(2)解:如图,设AD⊥BF于H,作DG⊥BC于G,则四边形BCDH是矩形.
∴DG=BH=BF.
∵BF=BC,BC=CD,
∴DG=CD.
在直角△CDG中,
∵∠0CD=90°,DG=CD,
∴∠C=30°,
∵BC∥AD,
∴∠ADC=180°-∠C=150°.
