北师大版九年级数学上册2.3公式法求解一元二次方程(第一课时)课件(18张)
文档属性
| 名称 | 北师大版九年级数学上册2.3公式法求解一元二次方程(第一课时)课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 00:00:00 | ||
图片预览






文档简介
课件18张PPT。1.会用配方法推导一元二次方程的求根公式。
2.掌握用公式法解一元二次方程。
3.理解根的判别式, 会判断一个一元二次方程根的情况。
4.根据根的判别式值的情况,体会数学分类思想。学习目标配方法解一元二次方程的一般步骤: (1)化—化二次项系数为1;(2)移—移项,使得方程左边为二次项和一次项,右边为常数项;(3)配—配方,方程两边都加上一次项系数一半
的平方;(4)开—如果方程的右边是非负数,就可左右两边
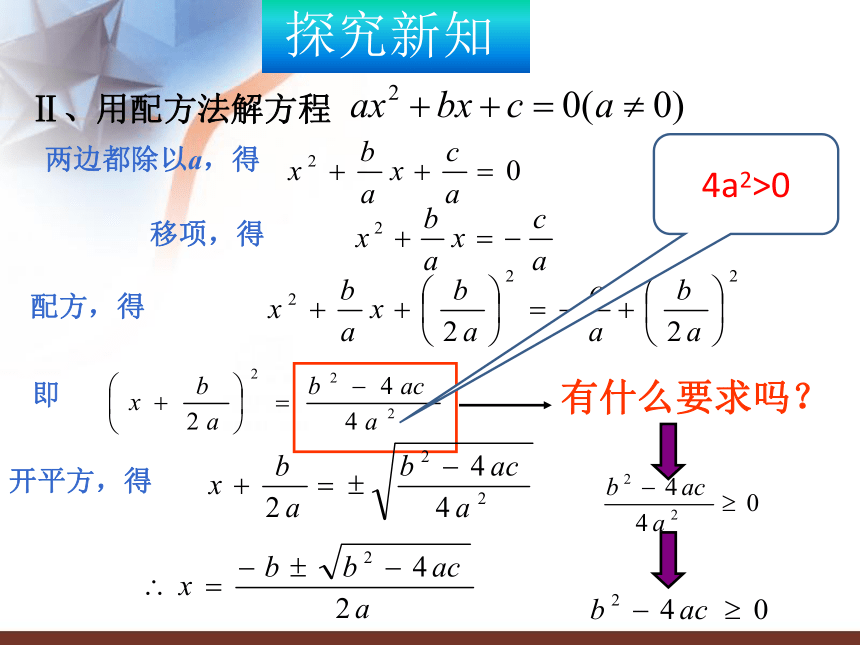
开平方 ; (5)解—解一元二次方程。复习回顾用配方法解方程:移项,得两边都除以2,得配方,得开平方,得 复习回顾Ⅱ、用配方法解方程 移项,得两边都除以a,得配方,得即开平方,得有什么要求吗? 探究新知4a2>0公式法解一元二次方程: 一般地,对于一元二次方程
当 时,它的根是: 上面这个式子称为一元二次方程的求根公式。
用求根公式解一元二次方程的方法称为公式法。b2-4ac<0时呢? 要点呈现 尝试新法 用公式法解方程解:a=2 b=-1 c=-4x 1=x2=例 解方程:(2)解:化简为一般式:这里 a=4, b= -4 , c= 1.∵b2 - 4ac=( )2 - 4×4×1=0,即:x 1= x2=范例讲解范例范例讲解
讲解 尝试新法
例 解方程 : 尝试新法 解: (1)x 2-7 x -18=0C=-18解方程:( x -2)(1-3 x)=6.这里 a=3, b= -7, c= 8.∵b2 - 4ac=(-7)2 - 4×3×8=49 - 96= - 47< 0,∴原方程没有实数根.解:去括号: x -2-3 x 2+6 x =6,化简为一般式:-3 x 2+7 x -8=0,3 x 2-7 x +8=0, 尝试新法1.化成一般形式,写出a,b,c的值;2.再求出b2-4ac的值;3.最后代入公式:当 b2-4ac≥0时,方程有两个的实数根; 当 b2-4ac<0时, 方程无实数根. 师生感悟 师生感悟 所以一元二次方程 的根的情况可由b2-4ac来确定,根据b2-4ac的值的符号,可以确定一元二次方程根的情况.
即有:b2-4ac >0方程有两个不相等的实数根b2-4ac =0方程有两个相等的实数根b2-4ac<0方程没有实数根一元二次方程 课堂检测有两个不相等的实数根有两个相等的实数根无解有两个实数根 有两个不相等的实数根△>0△=0△<0△ ≥0△>0△?0△的符号抢答题:根据根的判别式判定根的情况无解 课堂检测用公式法解下列关于x 的方程,(做完后同学间相互交流)
(1)2 x 2+4 x -1=0 (2)x ( x -6)+9=0
(3) 4x 2- x +3 =0 (4) 2x2-5mx-3m2=0(m>0)
△>0△=0△?0△?0 总结提高
(1).第43页随堂练习1,2,3,
(2).思考与探究:对于求根公式的推导,若一元二次方程a x2+b x+c=0(a≠0) ,方程的两边都乘以4a,你能推导出一元二次方程的求根公式吗?试试看,这种推导方法与教材上的方法有什么异同?你认为哪一种方法好?
课后作业谢谢!谢谢各位老师的指导!祝同学们学习愉快!
2.掌握用公式法解一元二次方程。
3.理解根的判别式, 会判断一个一元二次方程根的情况。
4.根据根的判别式值的情况,体会数学分类思想。学习目标配方法解一元二次方程的一般步骤: (1)化—化二次项系数为1;(2)移—移项,使得方程左边为二次项和一次项,右边为常数项;(3)配—配方,方程两边都加上一次项系数一半
的平方;(4)开—如果方程的右边是非负数,就可左右两边
开平方 ; (5)解—解一元二次方程。复习回顾用配方法解方程:移项,得两边都除以2,得配方,得开平方,得 复习回顾Ⅱ、用配方法解方程 移项,得两边都除以a,得配方,得即开平方,得有什么要求吗? 探究新知4a2>0公式法解一元二次方程: 一般地,对于一元二次方程
当 时,它的根是: 上面这个式子称为一元二次方程的求根公式。
用求根公式解一元二次方程的方法称为公式法。b2-4ac<0时呢? 要点呈现 尝试新法 用公式法解方程解:a=2 b=-1 c=-4x 1=x2=例 解方程:(2)解:化简为一般式:这里 a=4, b= -4 , c= 1.∵b2 - 4ac=( )2 - 4×4×1=0,即:x 1= x2=范例讲解范例范例讲解
讲解 尝试新法
例 解方程 : 尝试新法 解: (1)x 2-7 x -18=0C=-18解方程:( x -2)(1-3 x)=6.这里 a=3, b= -7, c= 8.∵b2 - 4ac=(-7)2 - 4×3×8=49 - 96= - 47< 0,∴原方程没有实数根.解:去括号: x -2-3 x 2+6 x =6,化简为一般式:-3 x 2+7 x -8=0,3 x 2-7 x +8=0, 尝试新法1.化成一般形式,写出a,b,c的值;2.再求出b2-4ac的值;3.最后代入公式:当 b2-4ac≥0时,方程有两个的实数根; 当 b2-4ac<0时, 方程无实数根. 师生感悟 师生感悟 所以一元二次方程 的根的情况可由b2-4ac来确定,根据b2-4ac的值的符号,可以确定一元二次方程根的情况.
即有:b2-4ac >0方程有两个不相等的实数根b2-4ac =0方程有两个相等的实数根b2-4ac<0方程没有实数根一元二次方程 课堂检测有两个不相等的实数根有两个相等的实数根无解有两个实数根 有两个不相等的实数根△>0△=0△<0△ ≥0△>0△?0△的符号抢答题:根据根的判别式判定根的情况无解 课堂检测用公式法解下列关于x 的方程,(做完后同学间相互交流)
(1)2 x 2+4 x -1=0 (2)x ( x -6)+9=0
(3) 4x 2- x +3 =0 (4) 2x2-5mx-3m2=0(m>0)
△>0△=0△?0△?0 总结提高
(1).第43页随堂练习1,2,3,
(2).思考与探究:对于求根公式的推导,若一元二次方程a x2+b x+c=0(a≠0) ,方程的两边都乘以4a,你能推导出一元二次方程的求根公式吗?试试看,这种推导方法与教材上的方法有什么异同?你认为哪一种方法好?
课后作业谢谢!谢谢各位老师的指导!祝同学们学习愉快!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
