北师大版九年级数学上册1.2矩形的性质1课件(17张)
文档属性
| 名称 | 北师大版九年级数学上册1.2矩形的性质1课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 27.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 14:54:16 | ||
图片预览




文档简介
课件17张PPT。 2.矩形的性质与判定
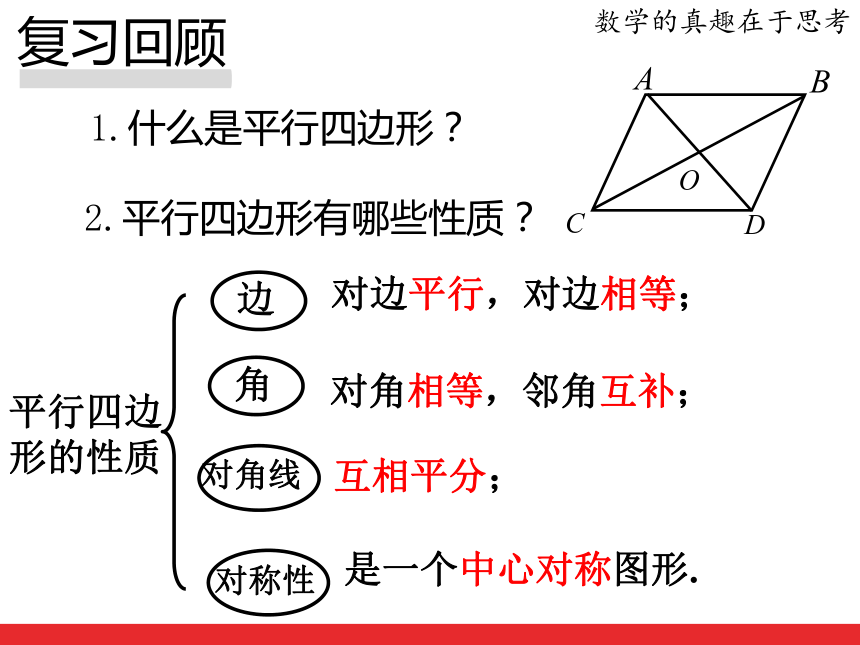
(第 1 课 时) 数学是思维的体操 是一个中心对称图形.对边平行,对边相等;互相平分;对角相等,邻角互补;1.什么是平行四边形?2.平行四边形有哪些性质?
复习回顾数学的真趣在于思考平行四边形的性质B
A
C
D
O
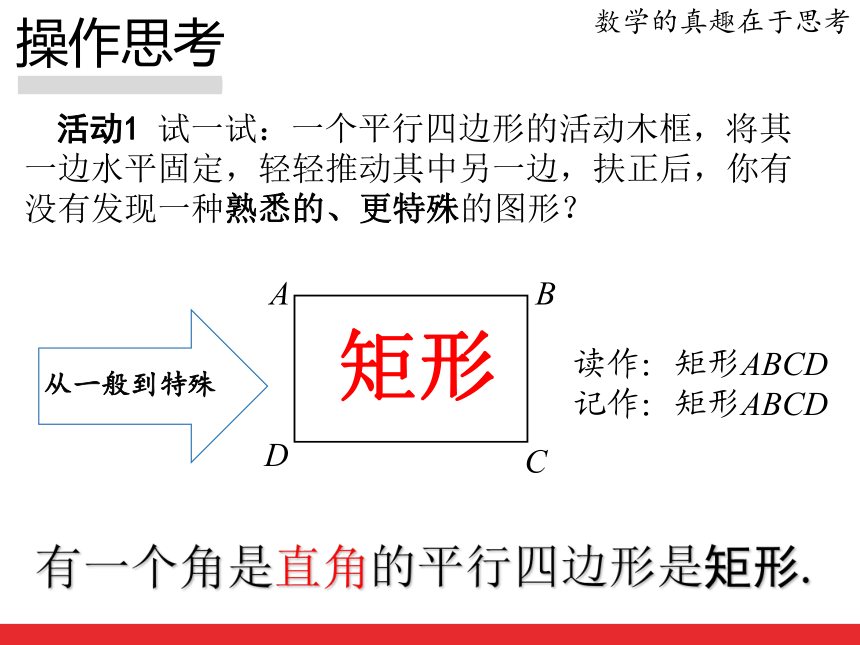
操作思考活动1 试一试:一个平行四边形的活动木框,将其一边水平固定,轻轻推动其中另一边,扶正后,你有没有发现一种熟悉的、更特殊的图形?数学的真趣在于思考矩形读作:矩形ABCD
记作:矩形ABCD
有一个角是直角的平行四边形是矩形.生活举例数学的真趣在于思考矩形是生活中常见图形,如:你还发现生活中有哪些是矩形的图案.活动2 在刚才的操作活动中,矩形是特殊的平行
四边形,那么矩形具有平行四边形的一切性质吗?性质探究猜想1:矩形的四个角都是 .数学的真趣在于思考直角矩形还具有哪些特殊的性质呢?我们用类比思想,先从边、角方面进行观察猜想,并与同伴交流.矩形具有平行四边形的一切性质.验证猜想:矩形的四个角都是直角.已知:如图,四边形ABCD是
平行四边形, 且∠A=90°.
求证:∠B=∠C=∠D=∠A=90°.几何语言表述为:∵四边形ABCD是矩形,
∴ ∠A=∠B=∠C=∠D=90°.定理 矩形的四个角都是直角.数学的真趣在于思考 性质探究
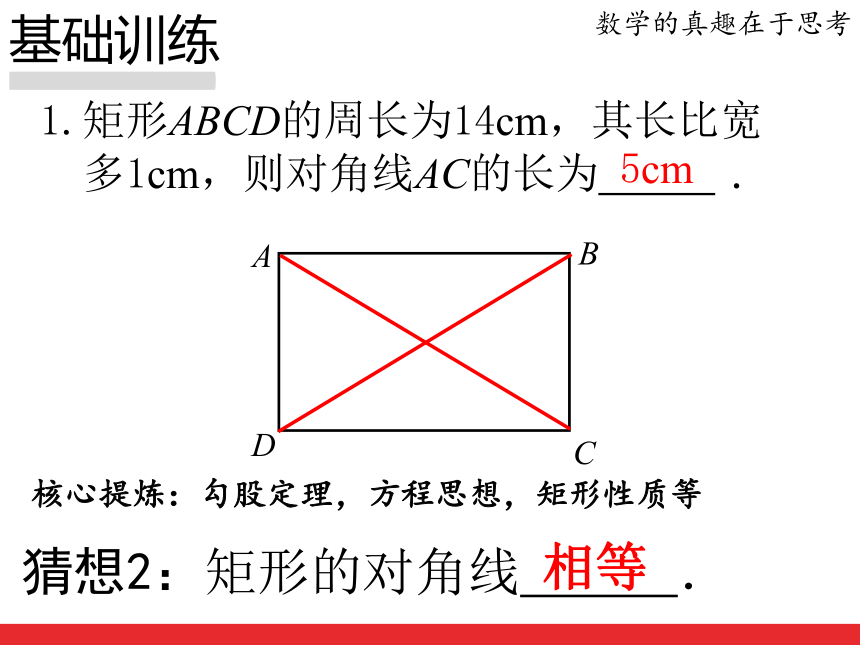
1.矩形ABCD的周长为14cm,其长比宽
多1cm,则对角线AC的长为 .基础训练数学的真趣在于思考猜想2:矩形的对角线 .相等5cm核心提炼:勾股定理,方程思想,矩形性质等已知:如图,四边形ABCD是矩形,求证:AC = BD.证明:在矩形ABCD中,
∵∠ABC=∠DCB=90°,
又∵AB = DC ,BC=CB,
∴△ABC≌△DCB.
∴AC=BD. 验证猜想:矩形的对角线相等.数学的真趣在于思考 定理 矩形的对角线相等.几何语言表述为:∵四边形ABCD是矩形,
∴AC=BD.性质探究O 2.如图,在矩形ABCD中,对角线AC与BD交 于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OD=ADD基础训练数学的真趣在于思考在矩形ABCD中,根据AC=BD,还能找到哪些相等的线段.又有哪些特殊的三角形.ABCDO通过折纸操作观察,思考矩形的对称性:矩形是中心对称图形,又是轴对称图形.矩形的对称中心在哪?矩形的2条对称轴有何特征?操作体验数学的真趣在于思考 3. 如图,EF过矩形ABCD对角线的交点O,分别交AB、CD于点E、F,那么阴影部分的面积是矩形ABCD面积的 .
基础训练数学的真趣在于思考核心提炼:整体思想,转化思想等矩形的性质数学的真趣在于思考归纳小结直角相等平分中心对称轴对称∵四边形ABCD是矩形,
∴∠DAB=∠ABC=∠BCD
=∠ADC=90°.
∵四边形ABCD是矩形,
∴AC=BD或
OA=OB=OC=OD.思考:如果将矩形ABCD沿AC剪掉一半,观察△ABC,你又会发现线段OB与AC存在怎样的等量关系?性质拓展数学的真趣在于思考定理 直角三角形斜边上的中线等于斜边的一半.D已知,OB是直角△ABC斜边
AC上的中线,求证:AC=2OB.CAO
BE提示:连中点,证垂直,或作垂直,证中点. 4. 如图,在△ABC中,∠C=90°,点D为AB的中点,点E在BC上,若CE=BD,∠DEC=70°,则∠B的度数为 .
能力测评数学的真趣在于思考40°(提示:连接CD,由直角三角形斜边上的中线等于斜边的一半,寻找等量后再解答) 2. 如图,在平面直角坐标系中,
直角△ABC三顶点的坐标分别是
A(-5,0)、B(3,n)、C(5,0).
(1)求n的值;
(2)在坐标系中取点D,使四边
形ABCD为矩形,画出矩形
并写出点D的坐标.
思维拓展数学的真趣在于思考4(-3,-4)Dy
x
B
C
A
O
整理收获 在探究学习矩形性质的过程中,
谈谈自己的所学所悟及数学思考?
数学的真趣在于思考 2.如图,在矩形ABCD中,两条对角线
交于点O,∠AOD=120°,AB=2.5cm,
(1)求矩形对角线的长;
(2)AE平分∠BAD交BC
于点E,求∠BOE的度数.
课后提升数学的真趣在于思考C1.数学课本P13页知识技能1.2.3;
数学思考:
(第 1 课 时) 数学是思维的体操 是一个中心对称图形.对边平行,对边相等;互相平分;对角相等,邻角互补;1.什么是平行四边形?2.平行四边形有哪些性质?
复习回顾数学的真趣在于思考平行四边形的性质B
A
C
D
O
操作思考活动1 试一试:一个平行四边形的活动木框,将其一边水平固定,轻轻推动其中另一边,扶正后,你有没有发现一种熟悉的、更特殊的图形?数学的真趣在于思考矩形读作:矩形ABCD
记作:矩形ABCD
有一个角是直角的平行四边形是矩形.生活举例数学的真趣在于思考矩形是生活中常见图形,如:你还发现生活中有哪些是矩形的图案.活动2 在刚才的操作活动中,矩形是特殊的平行
四边形,那么矩形具有平行四边形的一切性质吗?性质探究猜想1:矩形的四个角都是 .数学的真趣在于思考直角矩形还具有哪些特殊的性质呢?我们用类比思想,先从边、角方面进行观察猜想,并与同伴交流.矩形具有平行四边形的一切性质.验证猜想:矩形的四个角都是直角.已知:如图,四边形ABCD是
平行四边形, 且∠A=90°.
求证:∠B=∠C=∠D=∠A=90°.几何语言表述为:∵四边形ABCD是矩形,
∴ ∠A=∠B=∠C=∠D=90°.定理 矩形的四个角都是直角.数学的真趣在于思考 性质探究
1.矩形ABCD的周长为14cm,其长比宽
多1cm,则对角线AC的长为 .基础训练数学的真趣在于思考猜想2:矩形的对角线 .相等5cm核心提炼:勾股定理,方程思想,矩形性质等已知:如图,四边形ABCD是矩形,求证:AC = BD.证明:在矩形ABCD中,
∵∠ABC=∠DCB=90°,
又∵AB = DC ,BC=CB,
∴△ABC≌△DCB.
∴AC=BD. 验证猜想:矩形的对角线相等.数学的真趣在于思考 定理 矩形的对角线相等.几何语言表述为:∵四边形ABCD是矩形,
∴AC=BD.性质探究O 2.如图,在矩形ABCD中,对角线AC与BD交 于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OD=ADD基础训练数学的真趣在于思考在矩形ABCD中,根据AC=BD,还能找到哪些相等的线段.又有哪些特殊的三角形.ABCDO通过折纸操作观察,思考矩形的对称性:矩形是中心对称图形,又是轴对称图形.矩形的对称中心在哪?矩形的2条对称轴有何特征?操作体验数学的真趣在于思考 3. 如图,EF过矩形ABCD对角线的交点O,分别交AB、CD于点E、F,那么阴影部分的面积是矩形ABCD面积的 .
基础训练数学的真趣在于思考核心提炼:整体思想,转化思想等矩形的性质数学的真趣在于思考归纳小结直角相等平分中心对称轴对称∵四边形ABCD是矩形,
∴∠DAB=∠ABC=∠BCD
=∠ADC=90°.
∵四边形ABCD是矩形,
∴AC=BD或
OA=OB=OC=OD.思考:如果将矩形ABCD沿AC剪掉一半,观察△ABC,你又会发现线段OB与AC存在怎样的等量关系?性质拓展数学的真趣在于思考定理 直角三角形斜边上的中线等于斜边的一半.D已知,OB是直角△ABC斜边
AC上的中线,求证:AC=2OB.CAO
BE提示:连中点,证垂直,或作垂直,证中点. 4. 如图,在△ABC中,∠C=90°,点D为AB的中点,点E在BC上,若CE=BD,∠DEC=70°,则∠B的度数为 .
能力测评数学的真趣在于思考40°(提示:连接CD,由直角三角形斜边上的中线等于斜边的一半,寻找等量后再解答) 2. 如图,在平面直角坐标系中,
直角△ABC三顶点的坐标分别是
A(-5,0)、B(3,n)、C(5,0).
(1)求n的值;
(2)在坐标系中取点D,使四边
形ABCD为矩形,画出矩形
并写出点D的坐标.
思维拓展数学的真趣在于思考4(-3,-4)Dy
x
B
C
A
O
整理收获 在探究学习矩形性质的过程中,
谈谈自己的所学所悟及数学思考?
数学的真趣在于思考 2.如图,在矩形ABCD中,两条对角线
交于点O,∠AOD=120°,AB=2.5cm,
(1)求矩形对角线的长;
(2)AE平分∠BAD交BC
于点E,求∠BOE的度数.
课后提升数学的真趣在于思考C1.数学课本P13页知识技能1.2.3;
数学思考:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
