1.1.1正弦定理(共33张PPT)
文档属性
| 名称 | 1.1.1正弦定理(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 11:48:53 | ||
图片预览





文档简介
(共33张PPT)
在任意三角形中有大边对大角,小边对小角,那么我们能否得到边、角关系准确量化的表示呢?
a
b
c
研究∠A, ∠B, ∠C,a,b,c之间又怎么样的数量关系?不妨先从特殊的三角形:直角三角形开始.
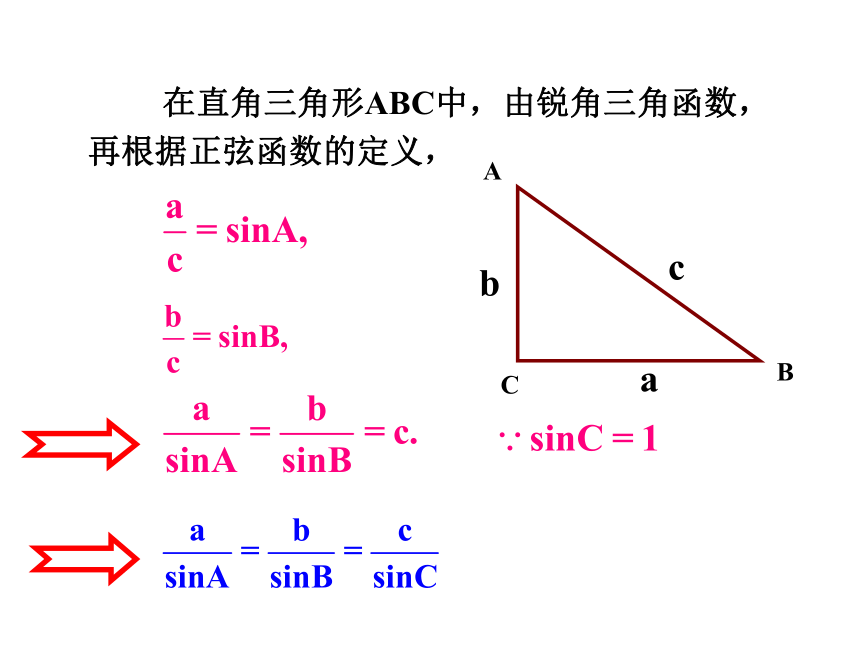
在直角三角形ABC中,由锐角三角函数,再根据正弦函数的定义,
a
b
c
思考
对于锐角三角形与钝角三角形,以上关系是否仍然成立?下面来看对于锐角三角形的情况.
D
∟
设边AC上的高是BD,则由三角函数定义:
a
b
c
E
∟
a
b
c
同理,在△ABC中,做边BC的高AE,
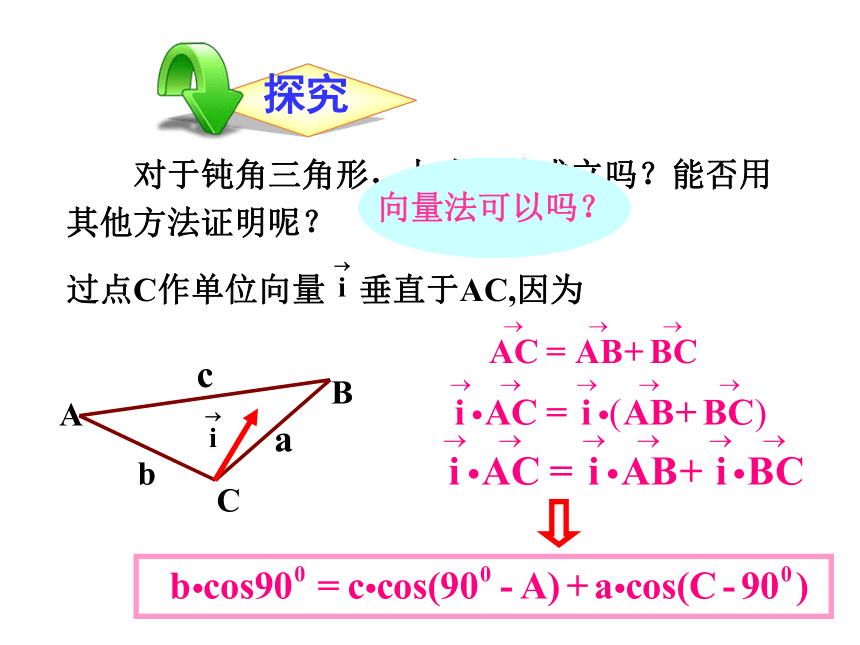
对于钝角三角形,上式仍然成立吗?能否用其他方法证明呢?
向量法可以吗?
a
b
c
还有其他方法吗?
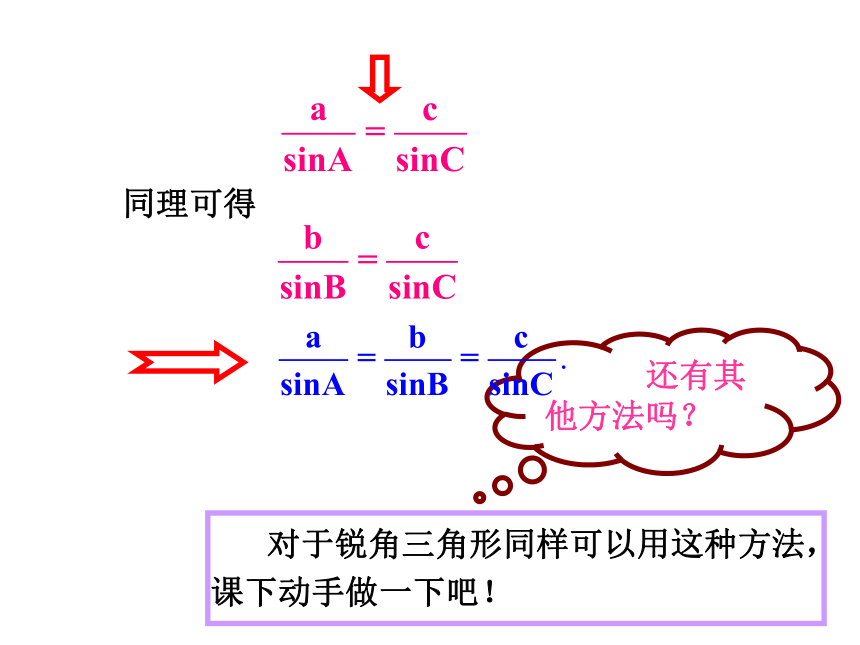
同理可得
对于锐角三角形同样可以用这种方法,课下动手做一下吧!
B(c cosA,c sinA)
右图1,以△ABC的顶点A为原点,边AC所在的射线为x轴的正半轴建立直角坐标系,顶点B的坐标是(ccosA,csinA). 则AC边上的高BE就是B点的纵坐标csinA,于是△ABC的面积:
同样可得
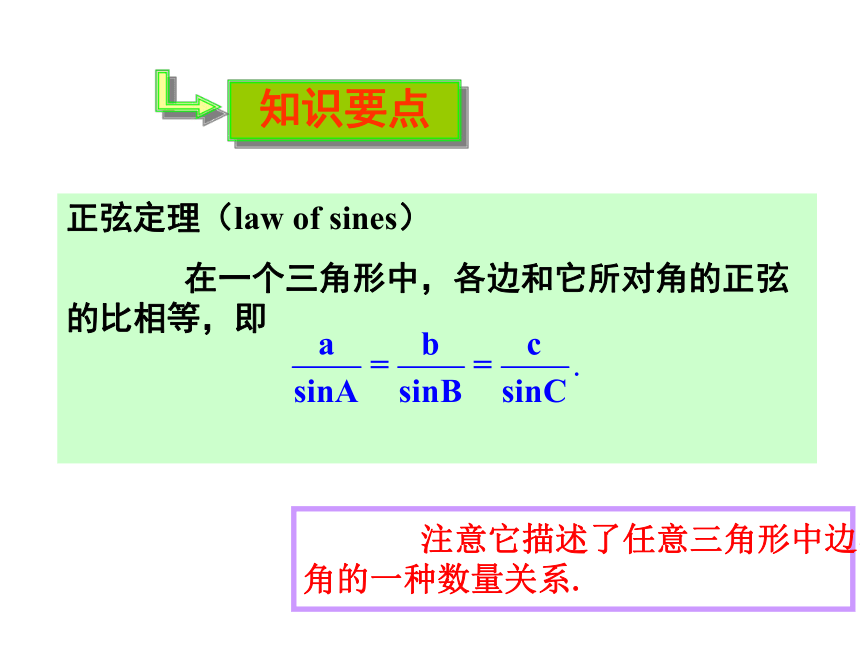
注意它描述了任意三角形中边与
角的一种数量关系.
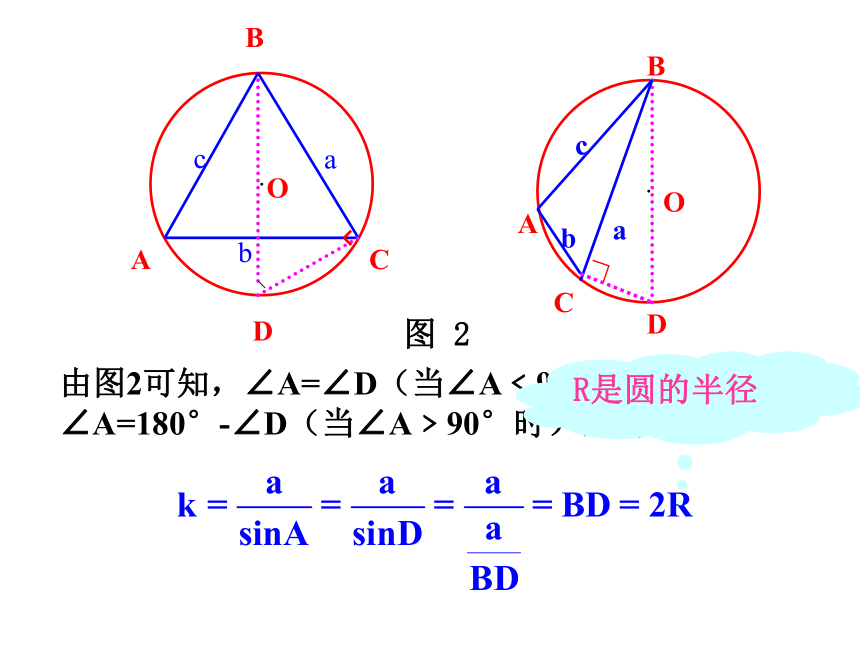
由图2可知,∠A=∠D(当∠A﹤90°时),∠A=180°-∠D(当∠A﹥90°时),所以
R是圆的半径
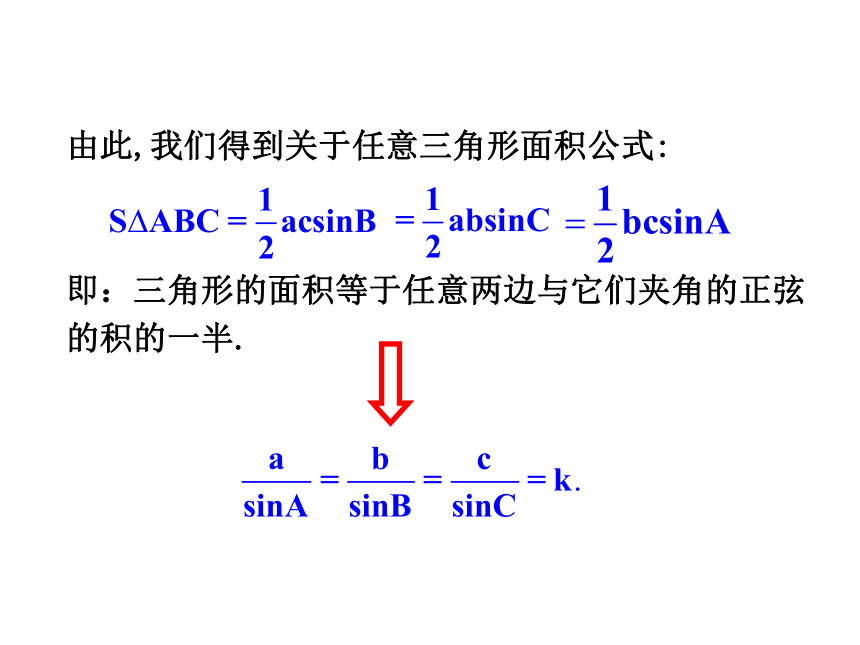
我们得到关于任意三角形边与角之间的关系的另一个重要定理:
正弦定理
在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素;
已知三角形的几个元素求其他元素的过程叫做解三角形(solving triangles).
利用正弦定理可以解决一些怎
么样的解三角形问题呢?
正弦定理可用于两类:
(1)已知三角形的任意两个角与一边,求其他两边与另一角;
(2)已知三角形的任意两边与其中一边的对角,计算其他的角与边.
有两解
无 解
有一解
无解
当A为锐角
当A为直角或钝角
2.解斜三角形
已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角.
1.正弦定理
1.(2017重庆)在△ABC中,
( )
A. B.
C. 2 D.
A
2.(19广东)已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=c=
,且∠A=75°,则b=( )
A.2 B.
C. D.
A
3.(17北京)在△ABC中,若 ,
C=150°,BC=1,则AB=___.
1.在△ABC中,(b+c):(c+a):(a+b)=4:5:6,则
7:5:3
D
CF,AE,BD都是三角形的高.
在任意三角形中有大边对大角,小边对小角,那么我们能否得到边、角关系准确量化的表示呢?
a
b
c
研究∠A, ∠B, ∠C,a,b,c之间又怎么样的数量关系?不妨先从特殊的三角形:直角三角形开始.
在直角三角形ABC中,由锐角三角函数,再根据正弦函数的定义,
a
b
c
思考
对于锐角三角形与钝角三角形,以上关系是否仍然成立?下面来看对于锐角三角形的情况.
D
∟
设边AC上的高是BD,则由三角函数定义:
a
b
c
E
∟
a
b
c
同理,在△ABC中,做边BC的高AE,
对于钝角三角形,上式仍然成立吗?能否用其他方法证明呢?
向量法可以吗?
a
b
c
还有其他方法吗?
同理可得
对于锐角三角形同样可以用这种方法,课下动手做一下吧!
B(c cosA,c sinA)
右图1,以△ABC的顶点A为原点,边AC所在的射线为x轴的正半轴建立直角坐标系,顶点B的坐标是(ccosA,csinA). 则AC边上的高BE就是B点的纵坐标csinA,于是△ABC的面积:
同样可得
注意它描述了任意三角形中边与
角的一种数量关系.
由图2可知,∠A=∠D(当∠A﹤90°时),∠A=180°-∠D(当∠A﹥90°时),所以
R是圆的半径
我们得到关于任意三角形边与角之间的关系的另一个重要定理:
正弦定理
在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素;
已知三角形的几个元素求其他元素的过程叫做解三角形(solving triangles).
利用正弦定理可以解决一些怎
么样的解三角形问题呢?
正弦定理可用于两类:
(1)已知三角形的任意两个角与一边,求其他两边与另一角;
(2)已知三角形的任意两边与其中一边的对角,计算其他的角与边.
有两解
无 解
有一解
无解
当A为锐角
当A为直角或钝角
2.解斜三角形
已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角.
1.正弦定理
1.(2017重庆)在△ABC中,
( )
A. B.
C. 2 D.
A
2.(19广东)已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=c=
,且∠A=75°,则b=( )
A.2 B.
C. D.
A
3.(17北京)在△ABC中,若 ,
C=150°,BC=1,则AB=___.
1.在△ABC中,(b+c):(c+a):(a+b)=4:5:6,则
7:5:3
D
CF,AE,BD都是三角形的高.
