2020年沪科新版九年级数学下册《第25章 投影与视图》单元测试卷(解析版)
文档属性
| 名称 | 2020年沪科新版九年级数学下册《第25章 投影与视图》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 15:18:24 | ||
图片预览

文档简介
2020年沪科新版九年级数学下册《第25章 投影与视图》单元测试卷
一.选择题(共12小题)
1.如图所示的正六棱柱的左视图是( )
A. B.
C. D.
2.如图所示的几何体的俯视图是( )
A. B. C. D.
3.有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加小正方体的个数为( )
A.2 B.3 C.4 D.5
4.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
5.如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
A.24 B.30 C.18 D.14.4
6.如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,你认为从左面看到的这个几何体的形状图是( )
A. B. C. D.
7.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
8.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
9.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A. B.
C. D.
10.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B.
C. D.
11.下列哪种光线形成的投影不是中心投影( )
A.探照灯 B.太阳 C.手电筒 D.路灯
12.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
二.填空题(共8小题)
13.一个四棱锥的俯视图是 .
14.苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 .
15.如图是五个相同的正方体堆成的几何体,则它的俯视图是 (填序号①,②等)
16.如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:
A图象是 号摄像机所拍,
B图象是 号摄像机所拍,
C图象是 号摄像机所拍,
D图象是 号摄像机所拍.
17.一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是 (填写一个即可).
18.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 个小立方块,最多需要 个小立方块.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
三.解答题(共8小题)
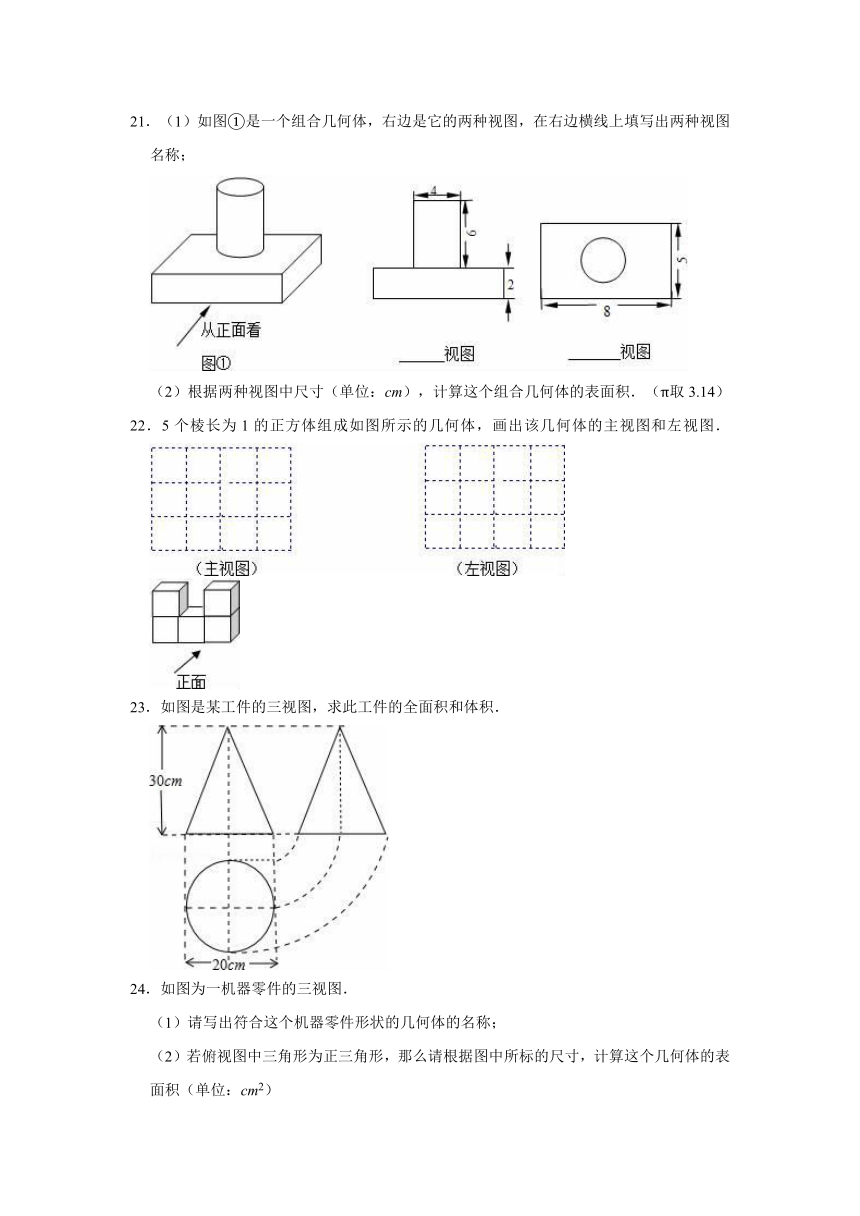
21.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
22.5个棱长为1的正方体组成如图所示的几何体,画出该几何体的主视图和左视图.
23.如图是某工件的三视图,求此工件的全面积和体积.
24.如图为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2)
25.如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请画出添加小正方体后所得几何体可能的左视图.
26.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 块小正方体.
27.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
28.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
2020年沪科新版九年级数学下册《第25章 投影与视图》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.如图所示的正六棱柱的左视图是( )
A. B.
C. D.
【分析】利用正六棱柱的形状结合三视图进而结合观察角度不同分别得出即可.
【解答】解:该几何体的三视图如图所示:
故选:C.
【点评】此题主要考查了画三视图,注意观察角度分别得出是解题关键.
2.如图所示的几何体的俯视图是( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上往下看,易得一个长方形,且其正中有一条纵向实线,
故选:B.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
3.有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加小正方体的个数为( )
A.2 B.3 C.4 D.5
【分析】若要保持俯视图和左视图不变,可以往第2排右侧正方体上添加1个,往第3排中间正方体上添加2个、右侧两个正方体上再添加1个,据此可得.
【解答】解:若要保持俯视图和左视图不变,可以往第2排右侧正方体上添加1个,往第3排中间正方体上添加2个、右侧两个正方体上再添加1个,
即一共添加4个小正方体,
故选:C.
【点评】本题考查简单组合体的三视图的画法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意看到的用实线表示,看不到的用虚线表示.
4.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得第一层有3个正方形,第二层最右边有一个正方形.
故选:A.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
5.如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
A.24 B.30 C.18 D.14.4
【分析】根据主视图、俯视图,根据立体图上的尺寸标注,求得左视图为长方形,其长为6,宽为,进而得到左视图的面积.
【解答】解:如图所示,根据俯视图中三角形的三边分别为3,4,5,
∴俯视图为直角三角形,且斜边为5,
故斜边上的高为=
∵左视图为长方形,其长为6,宽为,
∴左视图的面积=6×=14.4,
故选:D.
【点评】本题主要考查了由三视图判断几何体以及勾股定理的逆定理的运用,解决问题的关键是根据左视图的形状,求得左视图的面积.解题时注意:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
6.如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,你认为从左面看到的这个几何体的形状图是( )
A. B. C. D.
【分析】由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,据此可得左视图.
【解答】解:由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,
所以从左面看到的这个几何体的形状图是:
故选:D.
【点评】本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
7.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.依此即可解题.
【解答】解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
【点评】本题考查了三种视图及它的画法,看得到的棱画实线,看不到的棱画虚线.
8.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:根据题意:同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变.
故选:D.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应按照物体的外形即光线情况而定.
9.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A. B.
C. D.
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:当等边三角形木框与阳光平行时,投影是A;
当等边三角形木框与阳光有一定角度时,投影是C或D;
投影不可能是B.
故选:B.
【点评】本题主要考查对平行投影的理解和掌握,能熟练地观察图形得出正确结论是解此题的关键.
10.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B.
C. D.
【分析】平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例.
【解答】解:A、影子的方向不相同,错误;
B、影子平行,且较高的树的影子长度大于较低的树的影子,正确;
C、相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,错误;
D、影子的方向不相同,错误;
故选:B.
【点评】本题考查了平行投影,灵活运用平行投影的性质是解题关键.
11.下列哪种光线形成的投影不是中心投影( )
A.探照灯 B.太阳 C.手电筒 D.路灯
【分析】找到不是灯光的光源即可.
【解答】解:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有B选项得到的投影为平行投影,故选B.
【点评】解决本题的关键是理解中心投影的形成光源为灯光.
12.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
【分析】由题意易得,小阳和小明离光源是由远到近的过程,根据中心投影的特点,即可得到身影越来越短,而两人之间的距离始终与小阳的影长相等,则他们两人之间的距离越来越近.
【解答】解:因为小阳和小明两人从远处沿直线走到路灯下这一过程中离光源是由远到近的过程,所以他在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
【点评】本题综合考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
二.填空题(共8小题)
13.一个四棱锥的俯视图是 中间有点且该点与四边形四个顶点相连的图形 .
【分析】得到从上面看正四棱锥得到的平面图形即可.
【解答】解:一个四棱锥的俯视图中间有点且该点与四边形四个顶点相连的图形.
故答案为:中间有点且该点与四边形四个顶点相连的图形.
【点评】考查三视图中的俯视图知识:俯视图是从物体上面看得到的图形,注意锥顶,和所有看到的棱长都要表现在俯视图中.
14.苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 从不同的方向看同一物体看到的形状往往不同 .
【分析】诗句的意思是不同的角度看到的同一座山的风景也不同.
【解答】解:苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是从不同的方向看同一物体看到的形状不同.
故答案为:从不同的方向看同一物体看到的形状不
【点评】本题考查了几何体的视图的表现形式.
15.如图是五个相同的正方体堆成的几何体,则它的俯视图是 ① (填序号①,②等)
【分析】根据俯视图是从上面看到的图象判定则可.
【解答】解:从上面看几何体的左边是三个正方体,右边是一个正方体.故答案是①.
【点评】本题考查了三种视图中的俯视图,比较简单.
16.如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:
A图象是 2 号摄像机所拍,
B图象是 3 号摄像机所拍,
C图象是 4 号摄像机所拍,
D图象是 1 号摄像机所拍.
【分析】1号机正对壶柄,为D图形;
2号机看到的壶柄在右边,为A图形;
3号机的位置看不到壶柄,为B图形;
4号机看到的壶柄在左边,为C图形.
【解答】解:根据4个机器的不同位置可得到A图象是2号摄像机所拍,B图象是3号摄像机所拍,C图象是4号摄像机所拍,D图象是1号摄像机所拍.
【点评】解决本题的关键是抓住拍摄物体的一个特征得到位于不同位置所得到的不同图形.
17.一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是 正方体或球体(填一个即可) (填写一个即可).
【分析】三视图都相同的几何体是:正方体,三视图均为正方形;球体,三视图均为圆.
【解答】解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力和对立体图形的认识.
18.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 9 个小立方块,最多需要 13 个小立方块.
【分析】根据三视图的知识可得,几何体的底层确定有6个立方块,而第二层最少有2个立方块,最多会有4个.第三层最少要1个,最多要3个,故这个几何体最少要6+2+1个,最多要6+4+3个.
【解答】解:综合正视图和俯视图,这个几何体的底层最少要6个小立方块,最多也需要6个小立方块.第二层最少要2个小立方块,最多要4个,第三层最少要1个,最多要3个,因此这样的几何体最少要6+2+1=9个,最多要6+4+3=13个.
故答案为9,13
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 11 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
【分析】(1)根据如图所示即可得出图中小正方体的个数;
(2)读图可得,左视图有2列,每列小正方形数目分别为2,2;俯视图有4列,每行小正方形数目分别为2,2,1,1.
【解答】解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
【点评】此题主要考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 略 .
【分析】由左视图可以知道,左边应该为三个小立方体,且在正前方,添加即可.
【解答】解:
【点评】此题主要考查三视图的画图、学生的观察能力和空间想象能力.
三.解答题(共8小题)
21.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体表面积+上面圆柱的侧面积.
【解答】解:(1)如图所示:
;
(2)表面积=2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
22.5个棱长为1的正方体组成如图所示的几何体,画出该几何体的主视图和左视图.
【分析】根据主视图是从正面观看得出的图形,左视图是从左边看得出的图形,从而将看到的图形画出来即可.
【解答】解:所画图形如下所示:
【点评】此题考查了简单组合体的三视图,解答本题的关键是掌握三视图的查找办法,属于基础题,难度一般.
23.如图是某工件的三视图,求此工件的全面积和体积.
【分析】由三视图可知,该工件为底面半径为10cm,高为30cm的圆锥体,然后由勾股定理得到该圆锥的母线长,再由圆锥的侧面积和圆锥的底面积相加为圆锥的全面积;根据圆锥的体积公式可求圆锥的体积.
【解答】解:由三视图可知,该工件为底面半径为10cm,高为30cm的圆锥体,
这圆锥的母线长为=10(cm),
圆锥的侧面积为s=πrl=×20π×10=100π (cm2),
圆锥的底面积为102π=100πcm2,
圆锥的全面积为100π+100π=100(1+)π(cm2);
圆锥的体积×π×(20÷2)2×30=1000π(cm3).
故此工件的全面积是100(1+)πcm2,体积是1000πcm3.
【点评】本题主要考查几何物体三视图及圆锥的面积和体积求法.三视图判断几何体的形状是难点,这就要求掌握几种常见几何体的三视图,并建立三视图与实物的对应关系.
24.如图为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2)
【分析】(1)有2个视图的轮廓是长方形,那么这个几何体为棱柱,另一个视图是三角形,那么该几何体为三棱柱;
(2)根据正三角形一边上的高可得正三角形的边长,表面积=侧面积+2个底面积=底面周长×高+2个底面积.
【解答】解:(1)符合这个零件的几何体是直三棱柱;
(2)∵△ABC是正三角形,
又∵CD⊥AB,CD=2,
∴AC==4,
∴S表面积=4×2×3+2×4××2,
=24+8(cm2).
【点评】考查由三视图判断几何体及几何体表面积的计算;得到几何体的形状是解决本题的突破点;得到底面的边长是解决本题的易错点.
25.如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请画出添加小正方体后所得几何体可能的左视图.
【分析】(1)左视图有两列,小正方形的个数分别是3,1;俯视图有两排,上面一排有4个小正方形,下面一排有2个小正方形;
(2)根据题意可得此正方体应该添加在前排第2个小正方体上,进而可得左视图.
【解答】解:(1)如图所示:
;
(2)添加后可得如图所示的几何体:
,
左视图分别是:
.
【点评】此题主要考查了画三视图,关键是掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
26.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 6 块小正方体.
【分析】(1)左视图有2列,每列小正方数形数目分别为3,1,俯视图有4列,每列小正方形数目分别为2,1,1,1.据此可画出图形.
(2)持俯视图和左视图不变,可以在第1列后面一排添加2个,第3列添加2个,第4列添加2个,最多添加6个小正方体.
【解答】解:(1)如图所示:
;
(2)保持俯视图和左视图不变,最多可以再添加6块小正方体,
故答案为:6.
【点评】此题主要考查了作三视图,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
27.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
【分析】(1)根据光线相交于一点得出确定路灯的位置;
(2)利用AB,DE,确定大树的高,
(3)运用视角连接AD,即可得出能否看见大树.
【解答】解:(1)根据光线相交于一点,即可得出路灯确定路灯的位置;
(2)如图所示:
(3)如图所示,小明的眼睛近似地看成是点D,小明不能看见大树.
【点评】此题主要考查了平行投影与中心投影以及视角问题,根据已知确定住P点的位置是解决问题的关键.
28.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
【分析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系.计算可得DE=10(m).
【解答】解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴,
∴
∴DE=10(m).
说明:画图时,不要求学生做文字说明,只要画出两条平行线AC和DF,再连接EF即可.
【点评】本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例.要求学生通过投影的知识并结合图形解题.
一.选择题(共12小题)
1.如图所示的正六棱柱的左视图是( )
A. B.
C. D.
2.如图所示的几何体的俯视图是( )
A. B. C. D.
3.有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加小正方体的个数为( )
A.2 B.3 C.4 D.5
4.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
5.如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
A.24 B.30 C.18 D.14.4
6.如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,你认为从左面看到的这个几何体的形状图是( )
A. B. C. D.
7.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
8.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
9.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A. B.
C. D.
10.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B.
C. D.
11.下列哪种光线形成的投影不是中心投影( )
A.探照灯 B.太阳 C.手电筒 D.路灯
12.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
二.填空题(共8小题)
13.一个四棱锥的俯视图是 .
14.苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 .
15.如图是五个相同的正方体堆成的几何体,则它的俯视图是 (填序号①,②等)
16.如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:
A图象是 号摄像机所拍,
B图象是 号摄像机所拍,
C图象是 号摄像机所拍,
D图象是 号摄像机所拍.
17.一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是 (填写一个即可).
18.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 个小立方块,最多需要 个小立方块.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
三.解答题(共8小题)
21.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
22.5个棱长为1的正方体组成如图所示的几何体,画出该几何体的主视图和左视图.
23.如图是某工件的三视图,求此工件的全面积和体积.
24.如图为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2)
25.如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请画出添加小正方体后所得几何体可能的左视图.
26.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 块小正方体.
27.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
28.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
2020年沪科新版九年级数学下册《第25章 投影与视图》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.如图所示的正六棱柱的左视图是( )
A. B.
C. D.
【分析】利用正六棱柱的形状结合三视图进而结合观察角度不同分别得出即可.
【解答】解:该几何体的三视图如图所示:
故选:C.
【点评】此题主要考查了画三视图,注意观察角度分别得出是解题关键.
2.如图所示的几何体的俯视图是( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上往下看,易得一个长方形,且其正中有一条纵向实线,
故选:B.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
3.有若干个完全相同的小正方体堆成一个如图所示几何体,若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加小正方体的个数为( )
A.2 B.3 C.4 D.5
【分析】若要保持俯视图和左视图不变,可以往第2排右侧正方体上添加1个,往第3排中间正方体上添加2个、右侧两个正方体上再添加1个,据此可得.
【解答】解:若要保持俯视图和左视图不变,可以往第2排右侧正方体上添加1个,往第3排中间正方体上添加2个、右侧两个正方体上再添加1个,
即一共添加4个小正方体,
故选:C.
【点评】本题考查简单组合体的三视图的画法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意看到的用实线表示,看不到的用虚线表示.
4.如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是( )
A. B.
C. D.
【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:从上面看易得第一层有3个正方形,第二层最右边有一个正方形.
故选:A.
【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
5.如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
A.24 B.30 C.18 D.14.4
【分析】根据主视图、俯视图,根据立体图上的尺寸标注,求得左视图为长方形,其长为6,宽为,进而得到左视图的面积.
【解答】解:如图所示,根据俯视图中三角形的三边分别为3,4,5,
∴俯视图为直角三角形,且斜边为5,
故斜边上的高为=
∵左视图为长方形,其长为6,宽为,
∴左视图的面积=6×=14.4,
故选:D.
【点评】本题主要考查了由三视图判断几何体以及勾股定理的逆定理的运用,解决问题的关键是根据左视图的形状,求得左视图的面积.解题时注意:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
6.如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,你认为从左面看到的这个几何体的形状图是( )
A. B. C. D.
【分析】由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,据此可得左视图.
【解答】解:由俯视图知该几何体共2列,其中第1列前一排1个正方形、后1排2个正方形,第2列只有前排2个正方形,
所以从左面看到的这个几何体的形状图是:
故选:D.
【点评】本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
7.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.依此即可解题.
【解答】解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
【点评】本题考查了三种视图及它的画法,看得到的棱画实线,看不到的棱画虚线.
8.圆形的物体在太阳光的投影下是( )
A.圆形 B.椭圆形
C.线段 D.以上都有可能
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:根据题意:同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变.
故选:D.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应按照物体的外形即光线情况而定.
9.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A. B.
C. D.
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:当等边三角形木框与阳光平行时,投影是A;
当等边三角形木框与阳光有一定角度时,投影是C或D;
投影不可能是B.
故选:B.
【点评】本题主要考查对平行投影的理解和掌握,能熟练地观察图形得出正确结论是解此题的关键.
10.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B.
C. D.
【分析】平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例.
【解答】解:A、影子的方向不相同,错误;
B、影子平行,且较高的树的影子长度大于较低的树的影子,正确;
C、相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,错误;
D、影子的方向不相同,错误;
故选:B.
【点评】本题考查了平行投影,灵活运用平行投影的性质是解题关键.
11.下列哪种光线形成的投影不是中心投影( )
A.探照灯 B.太阳 C.手电筒 D.路灯
【分析】找到不是灯光的光源即可.
【解答】解:中心投影的光源为灯光,平行投影的光源为阳光与月光,在各选项中只有B选项得到的投影为平行投影,故选B.
【点评】解决本题的关键是理解中心投影的形成光源为灯光.
12.小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )
A.始终不变 B.越来越远 C.时近时远 D.越来越近
【分析】由题意易得,小阳和小明离光源是由远到近的过程,根据中心投影的特点,即可得到身影越来越短,而两人之间的距离始终与小阳的影长相等,则他们两人之间的距离越来越近.
【解答】解:因为小阳和小明两人从远处沿直线走到路灯下这一过程中离光源是由远到近的过程,所以他在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
【点评】本题综合考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
二.填空题(共8小题)
13.一个四棱锥的俯视图是 中间有点且该点与四边形四个顶点相连的图形 .
【分析】得到从上面看正四棱锥得到的平面图形即可.
【解答】解:一个四棱锥的俯视图中间有点且该点与四边形四个顶点相连的图形.
故答案为:中间有点且该点与四边形四个顶点相连的图形.
【点评】考查三视图中的俯视图知识:俯视图是从物体上面看得到的图形,注意锥顶,和所有看到的棱长都要表现在俯视图中.
14.苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是 从不同的方向看同一物体看到的形状往往不同 .
【分析】诗句的意思是不同的角度看到的同一座山的风景也不同.
【解答】解:苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是从不同的方向看同一物体看到的形状不同.
故答案为:从不同的方向看同一物体看到的形状不
【点评】本题考查了几何体的视图的表现形式.
15.如图是五个相同的正方体堆成的几何体,则它的俯视图是 ① (填序号①,②等)
【分析】根据俯视图是从上面看到的图象判定则可.
【解答】解:从上面看几何体的左边是三个正方体,右边是一个正方体.故答案是①.
【点评】本题考查了三种视图中的俯视图,比较简单.
16.如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则:
A图象是 2 号摄像机所拍,
B图象是 3 号摄像机所拍,
C图象是 4 号摄像机所拍,
D图象是 1 号摄像机所拍.
【分析】1号机正对壶柄,为D图形;
2号机看到的壶柄在右边,为A图形;
3号机的位置看不到壶柄,为B图形;
4号机看到的壶柄在左边,为C图形.
【解答】解:根据4个机器的不同位置可得到A图象是2号摄像机所拍,B图象是3号摄像机所拍,C图象是4号摄像机所拍,D图象是1号摄像机所拍.
【点评】解决本题的关键是抓住拍摄物体的一个特征得到位于不同位置所得到的不同图形.
17.一个几何体的主视图,左视图,俯视图都是同一个图形,那么这个几何体形状可能是 正方体或球体(填一个即可) (填写一个即可).
【分析】三视图都相同的几何体是:正方体,三视图均为正方形;球体,三视图均为圆.
【解答】解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
【点评】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力和对立体图形的认识.
18.用小立方块搭一个几何体,如图所示,这样的几何体最少需要 9 个小立方块,最多需要 13 个小立方块.
【分析】根据三视图的知识可得,几何体的底层确定有6个立方块,而第二层最少有2个立方块,最多会有4个.第三层最少要1个,最多要3个,故这个几何体最少要6+2+1个,最多要6+4+3个.
【解答】解:综合正视图和俯视图,这个几何体的底层最少要6个小立方块,最多也需要6个小立方块.第二层最少要2个小立方块,最多要4个,第三层最少要1个,最多要3个,因此这样的几何体最少要6+2+1=9个,最多要6+4+3=13个.
故答案为9,13
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.
19.如图,是由一些大小相同的小正方体组合成的简单几何体
(1)图中有 11 块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.
【分析】(1)根据如图所示即可得出图中小正方体的个数;
(2)读图可得,左视图有2列,每列小正方形数目分别为2,2;俯视图有4列,每行小正方形数目分别为2,2,1,1.
【解答】解:(1)根据如图所示即可数出有11块小正方体;
(2)如图所示;左视图,俯视图分别如下图:
故答案为:(1)11.
【点评】此题主要考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 略 .
【分析】由左视图可以知道,左边应该为三个小立方体,且在正前方,添加即可.
【解答】解:
【点评】此题主要考查三视图的画图、学生的观察能力和空间想象能力.
三.解答题(共8小题)
21.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体表面积+上面圆柱的侧面积.
【解答】解:(1)如图所示:
;
(2)表面积=2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
22.5个棱长为1的正方体组成如图所示的几何体,画出该几何体的主视图和左视图.
【分析】根据主视图是从正面观看得出的图形,左视图是从左边看得出的图形,从而将看到的图形画出来即可.
【解答】解:所画图形如下所示:
【点评】此题考查了简单组合体的三视图,解答本题的关键是掌握三视图的查找办法,属于基础题,难度一般.
23.如图是某工件的三视图,求此工件的全面积和体积.
【分析】由三视图可知,该工件为底面半径为10cm,高为30cm的圆锥体,然后由勾股定理得到该圆锥的母线长,再由圆锥的侧面积和圆锥的底面积相加为圆锥的全面积;根据圆锥的体积公式可求圆锥的体积.
【解答】解:由三视图可知,该工件为底面半径为10cm,高为30cm的圆锥体,
这圆锥的母线长为=10(cm),
圆锥的侧面积为s=πrl=×20π×10=100π (cm2),
圆锥的底面积为102π=100πcm2,
圆锥的全面积为100π+100π=100(1+)π(cm2);
圆锥的体积×π×(20÷2)2×30=1000π(cm3).
故此工件的全面积是100(1+)πcm2,体积是1000πcm3.
【点评】本题主要考查几何物体三视图及圆锥的面积和体积求法.三视图判断几何体的形状是难点,这就要求掌握几种常见几何体的三视图,并建立三视图与实物的对应关系.
24.如图为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称;
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2)
【分析】(1)有2个视图的轮廓是长方形,那么这个几何体为棱柱,另一个视图是三角形,那么该几何体为三棱柱;
(2)根据正三角形一边上的高可得正三角形的边长,表面积=侧面积+2个底面积=底面周长×高+2个底面积.
【解答】解:(1)符合这个零件的几何体是直三棱柱;
(2)∵△ABC是正三角形,
又∵CD⊥AB,CD=2,
∴AC==4,
∴S表面积=4×2×3+2×4××2,
=24+8(cm2).
【点评】考查由三视图判断几何体及几何体表面积的计算;得到几何体的形状是解决本题的突破点;得到底面的边长是解决本题的易错点.
25.如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请画出添加小正方体后所得几何体可能的左视图.
【分析】(1)左视图有两列,小正方形的个数分别是3,1;俯视图有两排,上面一排有4个小正方形,下面一排有2个小正方形;
(2)根据题意可得此正方体应该添加在前排第2个小正方体上,进而可得左视图.
【解答】解:(1)如图所示:
;
(2)添加后可得如图所示的几何体:
,
左视图分别是:
.
【点评】此题主要考查了画三视图,关键是掌握在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
26.如图是由一些棱长都为1cm的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,最多可以再添加 6 块小正方体.
【分析】(1)左视图有2列,每列小正方数形数目分别为3,1,俯视图有4列,每列小正方形数目分别为2,1,1,1.据此可画出图形.
(2)持俯视图和左视图不变,可以在第1列后面一排添加2个,第3列添加2个,第4列添加2个,最多添加6个小正方体.
【解答】解:(1)如图所示:
;
(2)保持俯视图和左视图不变,最多可以再添加6块小正方体,
故答案为:6.
【点评】此题主要考查了作三视图,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
27.如图,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试判断是路灯还是太阳光,如果是路灯确定路灯的位置(用点P表示).如果是太阳光请画出光线.
(2)在图中画出表示大树高的线段.
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.
【分析】(1)根据光线相交于一点得出确定路灯的位置;
(2)利用AB,DE,确定大树的高,
(3)运用视角连接AD,即可得出能否看见大树.
【解答】解:(1)根据光线相交于一点,即可得出路灯确定路灯的位置;
(2)如图所示:
(3)如图所示,小明的眼睛近似地看成是点D,小明不能看见大树.
【点评】此题主要考查了平行投影与中心投影以及视角问题,根据已知确定住P点的位置是解决问题的关键.
28.已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
【分析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系.计算可得DE=10(m).
【解答】解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴,
∴
∴DE=10(m).
说明:画图时,不要求学生做文字说明,只要画出两条平行线AC和DF,再连接EF即可.
【点评】本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例.要求学生通过投影的知识并结合图形解题.
