2020年春基于核心素养中考物理特色专题——推导证明类问题含解析
文档属性
| 名称 | 2020年春基于核心素养中考物理特色专题——推导证明类问题含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-08 22:07:41 | ||
图片预览




文档简介
2020年春基于核心素养中考物理特色专题——推导证明类问题
证明推导题就是结合物理公式和物理规律,用数学的方法,导出一个要得到的等式。在证明过程中需要用到物理规律,所以灵活理解物理规律,应用物理规律是物理证明推导题的精神所致。光用数学办法得出的结论是不可靠的。初中阶段在证明题问题中,经常用到平衡力思想、光的反射定律、牛顿第三定律、串并联电路电流电压特点、重力与质量关系等,应用数学知识经常用到全等三角形、相似三角形、三角函数等。有时能正确做出图形是完成任务的重要保证。证明推导题在安徽省、天津市中考常出现,在河南省、河北省、以及湖北、山东等虽然没有直接要求证明推导,但在选择题、填空题、计算题里要用到推导的办法。所以这类问题也要十分关注。
【例题1】如图有两平面镜夹角为θ,有一束光线从C点射人经过两次反射从F点射出,证明其出射角
γ=2θ.
【答案】见解析。
【解析】三角形的一个外角等于和它不相邻的两个内角之和。
γ=∠FED+∠CDE
平角等于180°
所以∠FED=180°-2∠DEO
∠CDE=180°-2∠EDO
所以
γ=∠FED+∠CDE
=(180°-2∠DEO)+(180°-2∠EDO)
=360°-2(∠DEO +∠DEO)
在△EDO中,∠DEO +∠DEO=180°-θ
所以,
γ=360°-2(∠DEO +∠DEO)=360°-2(180°-θ)=2θ
所以γ=2θ.
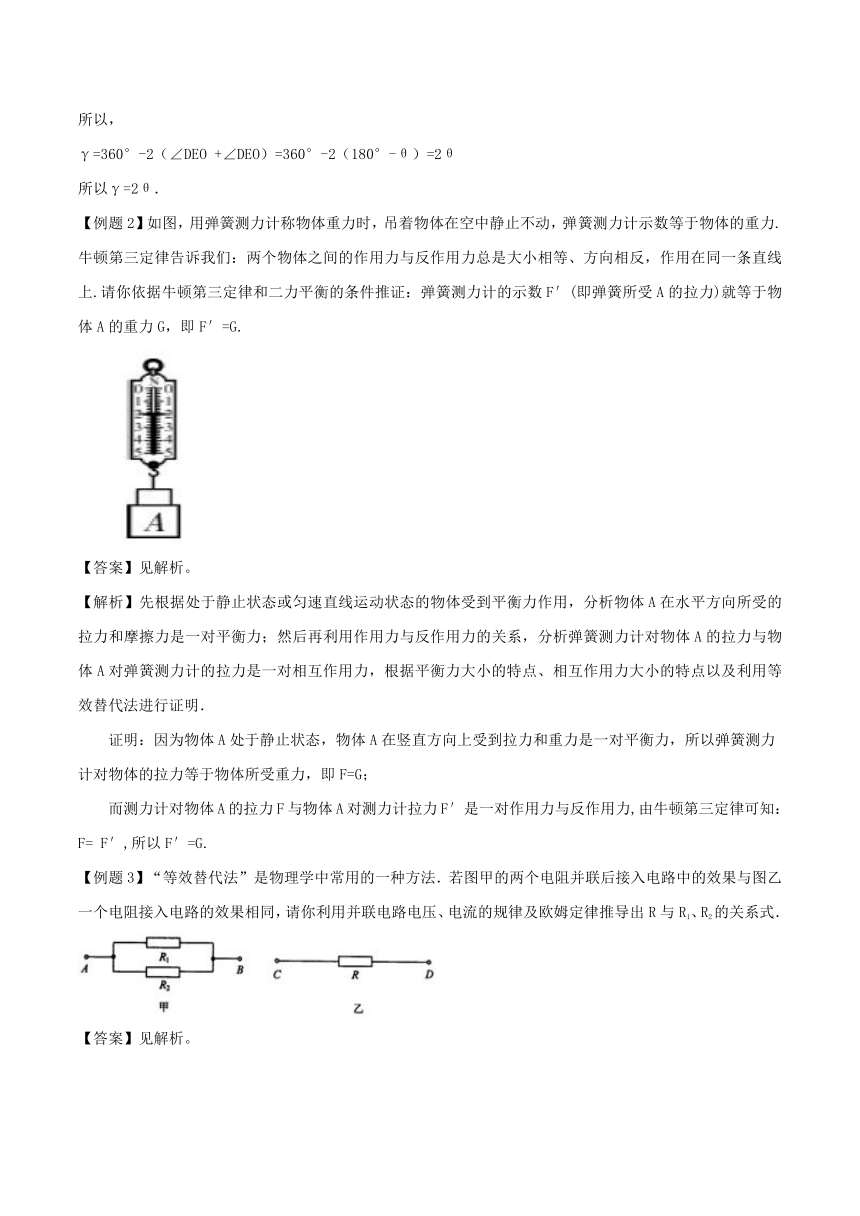
【例题2】如图,用弹簧测力计称物体重力时,吊着物体在空中静止不动,弹簧测力计示数等于物体的重力.牛顿第三定律告诉我们:两个物体之间的作用力与反作用力总是大小相等、方向相反,作用在同一条直线上.请你依据牛顿第三定律和二力平衡的条件推证:弹簧测力计的示数F′(即弹簧所受A的拉力)就等于物体A的重力G,即F′=G.
【答案】见解析。
【解析】先根据处于静止状态或匀速直线运动状态的物体受到平衡力作用,分析物体A在水平方向所受的拉力和摩擦力是一对平衡力;然后再利用作用力与反作用力的关系,分析弹簧测力计对物体A的拉力与物体A对弹簧测力计的拉力是一对相互作用力,根据平衡力大小的特点、相互作用力大小的特点以及利用等效替代法进行证明.
证明:因为物体A处于静止状态,物体A在竖直方向上受到拉力和重力是一对平衡力,所以弹簧测力计对物体的拉力等于物体所受重力,即F=G;
而测力计对物体A的拉力F与物体A对测力计拉力F′是一对作用力与反作用力,由牛顿第三定律可知:F= F′,所以F′=G.
【例题3】“等效替代法”是物理学中常用的一种方法.若图甲的两个电阻并联后接入电路中的效果与图乙一个电阻接入电路的效果相同,请你利用并联电路电压、电流的规律及欧姆定律推导出R与R1、R2的关系式.
【答案】见解析。
【解析】本题先利用欧姆定律得出并联电路中各电阻上的电流,然后将各电阻上的电流值,代入并联电路的电流关系式中,结合并联电路的电压特点即可导出R与R1、R2的关系式.
根据欧姆定律可得并联电路中两个电阻上的电流分别为:
I1=;I2=;一个电阻R上的电流为:I=;
由并联电路的电流关系I=I1+I2得:
=+;
又因为并联电路电压的特点是:U=U1=U2;
所以=+.
1.试根据压强是物体所受压力的大小与受力面积之比的定义,推导出密度为ρ的液体,在液面下深度为h处液体产生的压强P的表达式。(已知:重力与质量的比值为g,要求用ρ、h、g表示P)。
【答案】见解析。
【解析】设想液面下h深处有一面积为S的水平圆面,则水平圆面受到的压力:
F=G=mg=ρVg=ρShg,
则在液面下深度为h处液体产生的压强:
p===ρgh。
2.如图,AB两地相距4km,MN是与AB连线平行的一条小河的河岸,AB到河岸的垂直距离为3km,小军要从A处走到河岸取水然后送到B处,他先沿垂直于河岸的方向到D点取水然后再沿DB到B处。若小军的速度大小恒为5km/h,不考虑取水停留的时间。
(1)求小军完成这次取水和送水任务所想要的总时间。
(2)为了找到一条最短路线(即从A到河岸和从河岸到B的总路程最短),可以将MN看成一个平面镜,从A点作出一条光线经MN反射后恰能通过B点,请你证明入射点O即为最短路线的取水点。
【答案】
(1)1.6h;
如解析所述,入射点O为最短路线的取水点。
【解析】(1)如下图所示,小军通过的路程是AD+DB,
此时,AB=4km,AD=3km,根据勾股定理可知,DB=5km,
故小军通过的路程s=AD+DB=3km+5km=8km,
∵v=st
∴所需的时间:
t=sv=8km5km/h=1.6h;
(2)作出发光点A关于平面镜的对称点,即为像点A′,连接A′、B点交平面镜于点O,沿OB画出反射光线,连接AO画出入射光线,如图所示,图中O就是入射点;
①由图可知,A′B的连线是线段,两点之间,线段最短,即此时A′B之间的距离(A′O+OB)最短;
②根据平面镜成像的特点可知,此时AD=A′D,且Rt△ADO与Rt△A′DO有一条公共边DO,故可知Rt△ADO≌Rt△A′DO,即AO=A′O;
故AO+OB=A′O+OB;
即此时O点是最短路线的取水点。
3.如图所示,竖直放置平面镜MN前有一直立人体AB,人眼可通过平面镜观测到自己的像,试结合平面镜成像特点和光的反射原理推证:平面镜所需最小长度为人体长度的一半时,人眼即可观看到全身像.(设人眼在A点,不考虑成像宽度)
【答案】见解析。
【解析】根据平面镜成像特点作出像A′B′,分别连接AA′、AB′交平面镜于O′、O,人眼能看到像是因为物体发出的光经平面镜反射到人眼,再连接BO,可知人体最下端B发出的光可经O点反射到人眼,同样人体最上端A发出的光可经O′反射到人眼.如答图所示.
由平面镜成像特点可知:
又有,
所以在中是三角形的中位线,
所以
又知
故
4.已知水的比热容为C水,沙子的比热容的C沙,一堆干沙子和质量相同的水混合成为湿沙子,试推证湿沙子的比热为(C水+C沙) /2
【答案】见解析。
【解析】证明:假设湿沙子吸热后温度上升,那么其中所含干沙子吸收的热量为;所含水吸收的热量为,那么湿沙子的比热容:
,从而得证.
5.汽车沿着平直的公路从甲地开往乙地.
(1)若汽车在前一半路程的平均速度为v1,在后一半路程的平均速度为v2,则汽车全程的平均速度V为υ=2υ1υ2 ∕(υ1+υ2)
(2)若汽车在前一半路程和后一半路程所用时间相同,则全程平均速度V是多少?
【答案】见解析。
【解析】(1)设甲乙两地间的距离是2s,
则前半段与后半段的路程都是s,
∵v=st,
∴汽车的运动时间:t1=s/v1,t2=s/v2,
总的运动时间:t=t1+t2=s//v1+s/v2= s(1/v1+1/v2)=s v1 v2/(v1+v2)
全程的平均速度:v=2s/t=2s/ sv1v2/(v1+v2)
v =2v1 v2/(v1+ v2)
(2)前一半路程和后一半路程所用时间相同,
则t1=t2=s/v1=s/v2,则v1=v2,
全程的运动时间:t′=2t1=2s/v1=2s/v2,
全程的平均速度:v′=2s/t′=2s/2s/v2=v1=v2
6.一均匀的长方体浸没在液体中,如图所示.已知它的底面积为S,上表面所处深度为h1,下表面所处深度为h2,则长方体下表面所受到液体的压力表达式为 、浮力表达式为 .(液体密度ρ液和g为已知量)
【答案】ρ液gh2S;ρ液g(h2﹣h1)S.
【解析】由液体压强公式p=ρgh及压强公式的变形公式F=pS得:
F1=p1S=ρ液gh1S;
F2=p2S=ρ液gh2S,
F浮=F2﹣F1=ρ液gh2S﹣ρ液gh1S=ρ液g(h2﹣h1)S.
7.如图所示,用平行于斜面的力F,把重力为G的物体沿着长为L,高为h的斜面匀速拉到斜面顶端,这时物体受到的摩擦力大小为f,(η、F为已知,η为斜面的机械效率)试推导:f=F(1-η).
【答案】见解析。
【解析】根据η= W 有用/W 总,求出有用功大小,再根据W 总=W 有用+W 额求出克服摩擦力做的额外功的大小,根据W 额=fs求出摩擦力大小.
(1)∵η= W 有用/W 总,
∴W 有用=ηW 总=ηFs,
∵W 总=W 有用+W 额
∴W 额=W 总- W 有用=Fs-ηFs=(1-η)Fs=fs,
∴物体受到的摩擦力:f=F(1-η).
8.演绎式探究﹣探究太阳的引力系数:
(1)宇宙中任何两个物体之间都存在万有引力,万有引力的大小F引=G,其中m1、m2分别为两个物体间的距离,万有引力常数G=6.67×10﹣11N?m2/kg2.物体间引力和距离一定时,两个物体质量m1、m2分的关系可以用如图中图线 来表示.
(2)行星绕恒星的运动可以近似地看作匀速圆周运动.行星受到一个恒定的指向恒星的向心力,向心力的大小F向=mω2r,其中m为行星质量,r为两星之间的距离,ω为行星做圆周运动的角速度,其大小等于单位时间内行星与恒星连线转过的角度.行星绕恒星运动一周所用的时间用周期T表示,角速度ω与转动周期T的关系为:ω=.行星所受向心力F向的大小等于恒星对行星的引力F引的大小.
每个星球对在它表面附件的物体都存在引力,引力与物体质量的比值叫作引力系数,用g表示,我们学过地球的引力系数g地=10N/kg.对于每个星球来讲,下列公式成立:R2g=GM,其中R为星球半径,g为星球引力系数,M为星球质量,万有引力常数G=6.67×10﹣11N?m2/kg2.
已知地球质量为m,地球到太阳的距离为L,太阳半径为R,地球的公转周期为T.请你推导出太阳的引力系数g日=.
【答案】(1)b;(2)如解析所示.
【解析】根据万有引力的大小F引=G,分析其中已知量和不为的量和变化的量,可得两个物体质量m1、m2分的关系,从而确定图象;太阳为恒星,地球为太阳的行星,根据它们之间的万有引力公式和它们之间的向心力公式,结合对于太阳来讲,R2g=GM进行推导.
(1)万有引力的大小F引=G,其中m1、m2分别为两个物体间的距离,万有引力常数:
G=6.67×10﹣11N?m2/kg2.由上式可知:
物体间引力和距离一定时,两个物体质量m1、m2分之积为定值,为反比例函数的关系,故可以用如图中图线b来表示.
(2)地球为太阳的行星,根据万有引力公式,F引=G=G﹣﹣﹣﹣﹣①,
它们之间的向心力:
F向=mω2r=m﹣﹣﹣﹣﹣②;
因地球所受向心力F向的大小等于太阳对地球的引力F引的大小.由①②得:
F引=G=G=mL,
即GM=﹣﹣﹣﹣﹣﹣③;
又对于每个星球来讲,R2g日=GM,
g日=﹣﹣﹣﹣﹣④,将③代入④得:
太阳的引力系数g日=.
9.液体内部存在压强。如图所示,烧杯内盛有密度为的液体,我们可以设想液面下h深处有一面积为s的水平圆面,它所受到的压力是其上方圆柱形的小液柱所产生的。
(1)请在图中作出小液柱所受重力的示意图。
(2)请推证:液体内部深度为h处的压强。
【答案】见解析。
【解析】(1)如图
(2)小液柱的体积为:V=sh 小液柱的质量为:m=ρV=ρsh
小液柱的重力为:G=mg=ρshg
小液柱产生的压强为:p=F/s=G/s=ρshg /s=ρhg
即:液体内部深度为h处的压强p=ρhg
10.斜面是人们生产和生活中经常使用的一种可以省力的简单机械。下面是某同学针对斜面问题进行的理论研究的过程。请你帮他完成“理论论证”。
提出问题:使用斜面为什么可以省力?
建立模型:如图所示,斜面的长为L,高为h,沿光滑斜面匀速向上拉动重为G的物体,所用拉力为F。
理论论证:运用功的原理证明:F【答案】见解析。
【解析】将重为G的物体升高h,直接用手做的功W1=Gh,利用斜面做的功W2=FL,
根据功的原理W2=W1,FL=Gh,F=Gh/L,因为L>h,所以F11.在底面积为S的薄壁柱形容器内注入适量的水,让空烧杯漂浮在水面上,测出水的深度为h0,如图所示:再将一金属球放入烧杯中,此时烧杯仍漂浮在水面上,测出水的深为h1,最后将该金属球取出放入水中(空烧杯仍漂浮在水面上,待金属球沉底后测出水的深度为h2,已知水的密度为ρ水,请你推导:
(1)金属球的密度为ρ球= ρ水(h1-h0)/(h2-h0)
(2)金属球沉底后,它对容器底的压力为F=ρ水g(h1-h2)S 【答案】见解析。
【解析】金属球放入烧杯中,根据排开的液体体积增加量,利用阿基米德原理求出金属球的重力G球=△F浮,即可求其质量;将该金属球取出放入水中,此时排开的液体体积增加量,即为金属球的体积;最后即可根据ρ=求出金属球的密度;将该金属球取出放入水中,利用阿基米德原理求出金属球的浮力;它对容器底的压力F=G-F浮。
(1)当装有金属球的烧杯漂浮在盛有水的大容器的水面上,排开液体体积的增加量为△V排=S(h1-h0),
则由漂浮条件可得:G球=△F浮=ρ水△V排g=ρ水S(h1-h0)g,
所以,m球==ρ水S(h1-h0),
金属球投入水中后沉底,则V球=V排′=S(h2-h0),
所以,ρ球===ρ水;
(2)将该金属球取出放入水中后沉底,金属球受到的浮力:
F浮=ρ水V排′g=ρ水S(h2-h0)g,
则它对容器底的压力:
F=G球-F浮=ρ水S(h1-h0)g-ρ水S(h2-h0)g=ρ水g(h1-h2)S。
12.求证在串联电路中,串联电路的总电阻,等于各导体的电阻之和.
证明:根据流过串联电路各电阻的电流相等和串联电路两端的总电压等于各部分电路两端的电压之和,可得:
I=I1=I2=……=In …………(1)
U=U1+U2+……+Un …………(2)
根据欧姆定律:U=IR,U1=IR1, U2=IR2,…… Un=IRn…………(3)
把上述关系式代入(2)式,整理后可得:R=R1+R2+……+Rn
13.求证在并联电路中,并联电路总电阻的倒数,等于各个导体的电阻倒数之和.
证明:根据并联电路中各支路两端的电压相等和并联电路中的总电流等于各支路电流之和,可得:
U=U1=U2=……=Un ……… (1)
I=I1+I2+……+In …………(2)
由欧姆定律,I=U/R,I1=U1/R1,I2=U2/R2, ……,In=Un/Rn,代入(2)式并考虑到(1)式,得:
1/R=1/R1+1/R2+……1/Rn
证明推导题就是结合物理公式和物理规律,用数学的方法,导出一个要得到的等式。在证明过程中需要用到物理规律,所以灵活理解物理规律,应用物理规律是物理证明推导题的精神所致。光用数学办法得出的结论是不可靠的。初中阶段在证明题问题中,经常用到平衡力思想、光的反射定律、牛顿第三定律、串并联电路电流电压特点、重力与质量关系等,应用数学知识经常用到全等三角形、相似三角形、三角函数等。有时能正确做出图形是完成任务的重要保证。证明推导题在安徽省、天津市中考常出现,在河南省、河北省、以及湖北、山东等虽然没有直接要求证明推导,但在选择题、填空题、计算题里要用到推导的办法。所以这类问题也要十分关注。
【例题1】如图有两平面镜夹角为θ,有一束光线从C点射人经过两次反射从F点射出,证明其出射角
γ=2θ.
【答案】见解析。
【解析】三角形的一个外角等于和它不相邻的两个内角之和。
γ=∠FED+∠CDE
平角等于180°
所以∠FED=180°-2∠DEO
∠CDE=180°-2∠EDO
所以
γ=∠FED+∠CDE
=(180°-2∠DEO)+(180°-2∠EDO)
=360°-2(∠DEO +∠DEO)
在△EDO中,∠DEO +∠DEO=180°-θ
所以,
γ=360°-2(∠DEO +∠DEO)=360°-2(180°-θ)=2θ
所以γ=2θ.
【例题2】如图,用弹簧测力计称物体重力时,吊着物体在空中静止不动,弹簧测力计示数等于物体的重力.牛顿第三定律告诉我们:两个物体之间的作用力与反作用力总是大小相等、方向相反,作用在同一条直线上.请你依据牛顿第三定律和二力平衡的条件推证:弹簧测力计的示数F′(即弹簧所受A的拉力)就等于物体A的重力G,即F′=G.
【答案】见解析。
【解析】先根据处于静止状态或匀速直线运动状态的物体受到平衡力作用,分析物体A在水平方向所受的拉力和摩擦力是一对平衡力;然后再利用作用力与反作用力的关系,分析弹簧测力计对物体A的拉力与物体A对弹簧测力计的拉力是一对相互作用力,根据平衡力大小的特点、相互作用力大小的特点以及利用等效替代法进行证明.
证明:因为物体A处于静止状态,物体A在竖直方向上受到拉力和重力是一对平衡力,所以弹簧测力计对物体的拉力等于物体所受重力,即F=G;
而测力计对物体A的拉力F与物体A对测力计拉力F′是一对作用力与反作用力,由牛顿第三定律可知:F= F′,所以F′=G.
【例题3】“等效替代法”是物理学中常用的一种方法.若图甲的两个电阻并联后接入电路中的效果与图乙一个电阻接入电路的效果相同,请你利用并联电路电压、电流的规律及欧姆定律推导出R与R1、R2的关系式.
【答案】见解析。
【解析】本题先利用欧姆定律得出并联电路中各电阻上的电流,然后将各电阻上的电流值,代入并联电路的电流关系式中,结合并联电路的电压特点即可导出R与R1、R2的关系式.
根据欧姆定律可得并联电路中两个电阻上的电流分别为:
I1=;I2=;一个电阻R上的电流为:I=;
由并联电路的电流关系I=I1+I2得:
=+;
又因为并联电路电压的特点是:U=U1=U2;
所以=+.
1.试根据压强是物体所受压力的大小与受力面积之比的定义,推导出密度为ρ的液体,在液面下深度为h处液体产生的压强P的表达式。(已知:重力与质量的比值为g,要求用ρ、h、g表示P)。
【答案】见解析。
【解析】设想液面下h深处有一面积为S的水平圆面,则水平圆面受到的压力:
F=G=mg=ρVg=ρShg,
则在液面下深度为h处液体产生的压强:
p===ρgh。
2.如图,AB两地相距4km,MN是与AB连线平行的一条小河的河岸,AB到河岸的垂直距离为3km,小军要从A处走到河岸取水然后送到B处,他先沿垂直于河岸的方向到D点取水然后再沿DB到B处。若小军的速度大小恒为5km/h,不考虑取水停留的时间。
(1)求小军完成这次取水和送水任务所想要的总时间。
(2)为了找到一条最短路线(即从A到河岸和从河岸到B的总路程最短),可以将MN看成一个平面镜,从A点作出一条光线经MN反射后恰能通过B点,请你证明入射点O即为最短路线的取水点。
【答案】
(1)1.6h;
如解析所述,入射点O为最短路线的取水点。
【解析】(1)如下图所示,小军通过的路程是AD+DB,
此时,AB=4km,AD=3km,根据勾股定理可知,DB=5km,
故小军通过的路程s=AD+DB=3km+5km=8km,
∵v=st
∴所需的时间:
t=sv=8km5km/h=1.6h;
(2)作出发光点A关于平面镜的对称点,即为像点A′,连接A′、B点交平面镜于点O,沿OB画出反射光线,连接AO画出入射光线,如图所示,图中O就是入射点;
①由图可知,A′B的连线是线段,两点之间,线段最短,即此时A′B之间的距离(A′O+OB)最短;
②根据平面镜成像的特点可知,此时AD=A′D,且Rt△ADO与Rt△A′DO有一条公共边DO,故可知Rt△ADO≌Rt△A′DO,即AO=A′O;
故AO+OB=A′O+OB;
即此时O点是最短路线的取水点。
3.如图所示,竖直放置平面镜MN前有一直立人体AB,人眼可通过平面镜观测到自己的像,试结合平面镜成像特点和光的反射原理推证:平面镜所需最小长度为人体长度的一半时,人眼即可观看到全身像.(设人眼在A点,不考虑成像宽度)
【答案】见解析。
【解析】根据平面镜成像特点作出像A′B′,分别连接AA′、AB′交平面镜于O′、O,人眼能看到像是因为物体发出的光经平面镜反射到人眼,再连接BO,可知人体最下端B发出的光可经O点反射到人眼,同样人体最上端A发出的光可经O′反射到人眼.如答图所示.
由平面镜成像特点可知:
又有,
所以在中是三角形的中位线,
所以
又知
故
4.已知水的比热容为C水,沙子的比热容的C沙,一堆干沙子和质量相同的水混合成为湿沙子,试推证湿沙子的比热为(C水+C沙) /2
【答案】见解析。
【解析】证明:假设湿沙子吸热后温度上升,那么其中所含干沙子吸收的热量为;所含水吸收的热量为,那么湿沙子的比热容:
,从而得证.
5.汽车沿着平直的公路从甲地开往乙地.
(1)若汽车在前一半路程的平均速度为v1,在后一半路程的平均速度为v2,则汽车全程的平均速度V为υ=2υ1υ2 ∕(υ1+υ2)
(2)若汽车在前一半路程和后一半路程所用时间相同,则全程平均速度V是多少?
【答案】见解析。
【解析】(1)设甲乙两地间的距离是2s,
则前半段与后半段的路程都是s,
∵v=st,
∴汽车的运动时间:t1=s/v1,t2=s/v2,
总的运动时间:t=t1+t2=s//v1+s/v2= s(1/v1+1/v2)=s v1 v2/(v1+v2)
全程的平均速度:v=2s/t=2s/ sv1v2/(v1+v2)
v =2v1 v2/(v1+ v2)
(2)前一半路程和后一半路程所用时间相同,
则t1=t2=s/v1=s/v2,则v1=v2,
全程的运动时间:t′=2t1=2s/v1=2s/v2,
全程的平均速度:v′=2s/t′=2s/2s/v2=v1=v2
6.一均匀的长方体浸没在液体中,如图所示.已知它的底面积为S,上表面所处深度为h1,下表面所处深度为h2,则长方体下表面所受到液体的压力表达式为 、浮力表达式为 .(液体密度ρ液和g为已知量)
【答案】ρ液gh2S;ρ液g(h2﹣h1)S.
【解析】由液体压强公式p=ρgh及压强公式的变形公式F=pS得:
F1=p1S=ρ液gh1S;
F2=p2S=ρ液gh2S,
F浮=F2﹣F1=ρ液gh2S﹣ρ液gh1S=ρ液g(h2﹣h1)S.
7.如图所示,用平行于斜面的力F,把重力为G的物体沿着长为L,高为h的斜面匀速拉到斜面顶端,这时物体受到的摩擦力大小为f,(η、F为已知,η为斜面的机械效率)试推导:f=F(1-η).
【答案】见解析。
【解析】根据η= W 有用/W 总,求出有用功大小,再根据W 总=W 有用+W 额求出克服摩擦力做的额外功的大小,根据W 额=fs求出摩擦力大小.
(1)∵η= W 有用/W 总,
∴W 有用=ηW 总=ηFs,
∵W 总=W 有用+W 额
∴W 额=W 总- W 有用=Fs-ηFs=(1-η)Fs=fs,
∴物体受到的摩擦力:f=F(1-η).
8.演绎式探究﹣探究太阳的引力系数:
(1)宇宙中任何两个物体之间都存在万有引力,万有引力的大小F引=G,其中m1、m2分别为两个物体间的距离,万有引力常数G=6.67×10﹣11N?m2/kg2.物体间引力和距离一定时,两个物体质量m1、m2分的关系可以用如图中图线 来表示.
(2)行星绕恒星的运动可以近似地看作匀速圆周运动.行星受到一个恒定的指向恒星的向心力,向心力的大小F向=mω2r,其中m为行星质量,r为两星之间的距离,ω为行星做圆周运动的角速度,其大小等于单位时间内行星与恒星连线转过的角度.行星绕恒星运动一周所用的时间用周期T表示,角速度ω与转动周期T的关系为:ω=.行星所受向心力F向的大小等于恒星对行星的引力F引的大小.
每个星球对在它表面附件的物体都存在引力,引力与物体质量的比值叫作引力系数,用g表示,我们学过地球的引力系数g地=10N/kg.对于每个星球来讲,下列公式成立:R2g=GM,其中R为星球半径,g为星球引力系数,M为星球质量,万有引力常数G=6.67×10﹣11N?m2/kg2.
已知地球质量为m,地球到太阳的距离为L,太阳半径为R,地球的公转周期为T.请你推导出太阳的引力系数g日=.
【答案】(1)b;(2)如解析所示.
【解析】根据万有引力的大小F引=G,分析其中已知量和不为的量和变化的量,可得两个物体质量m1、m2分的关系,从而确定图象;太阳为恒星,地球为太阳的行星,根据它们之间的万有引力公式和它们之间的向心力公式,结合对于太阳来讲,R2g=GM进行推导.
(1)万有引力的大小F引=G,其中m1、m2分别为两个物体间的距离,万有引力常数:
G=6.67×10﹣11N?m2/kg2.由上式可知:
物体间引力和距离一定时,两个物体质量m1、m2分之积为定值,为反比例函数的关系,故可以用如图中图线b来表示.
(2)地球为太阳的行星,根据万有引力公式,F引=G=G﹣﹣﹣﹣﹣①,
它们之间的向心力:
F向=mω2r=m﹣﹣﹣﹣﹣②;
因地球所受向心力F向的大小等于太阳对地球的引力F引的大小.由①②得:
F引=G=G=mL,
即GM=﹣﹣﹣﹣﹣﹣③;
又对于每个星球来讲,R2g日=GM,
g日=﹣﹣﹣﹣﹣④,将③代入④得:
太阳的引力系数g日=.
9.液体内部存在压强。如图所示,烧杯内盛有密度为的液体,我们可以设想液面下h深处有一面积为s的水平圆面,它所受到的压力是其上方圆柱形的小液柱所产生的。
(1)请在图中作出小液柱所受重力的示意图。
(2)请推证:液体内部深度为h处的压强。
【答案】见解析。
【解析】(1)如图
(2)小液柱的体积为:V=sh 小液柱的质量为:m=ρV=ρsh
小液柱的重力为:G=mg=ρshg
小液柱产生的压强为:p=F/s=G/s=ρshg /s=ρhg
即:液体内部深度为h处的压强p=ρhg
10.斜面是人们生产和生活中经常使用的一种可以省力的简单机械。下面是某同学针对斜面问题进行的理论研究的过程。请你帮他完成“理论论证”。
提出问题:使用斜面为什么可以省力?
建立模型:如图所示,斜面的长为L,高为h,沿光滑斜面匀速向上拉动重为G的物体,所用拉力为F。
理论论证:运用功的原理证明:F
【解析】将重为G的物体升高h,直接用手做的功W1=Gh,利用斜面做的功W2=FL,
根据功的原理W2=W1,FL=Gh,F=Gh/L,因为L>h,所以F
(1)金属球的密度为ρ球= ρ水(h1-h0)/(h2-h0)
(2)金属球沉底后,它对容器底的压力为F=ρ水g(h1-h2)S 【答案】见解析。
【解析】金属球放入烧杯中,根据排开的液体体积增加量,利用阿基米德原理求出金属球的重力G球=△F浮,即可求其质量;将该金属球取出放入水中,此时排开的液体体积增加量,即为金属球的体积;最后即可根据ρ=求出金属球的密度;将该金属球取出放入水中,利用阿基米德原理求出金属球的浮力;它对容器底的压力F=G-F浮。
(1)当装有金属球的烧杯漂浮在盛有水的大容器的水面上,排开液体体积的增加量为△V排=S(h1-h0),
则由漂浮条件可得:G球=△F浮=ρ水△V排g=ρ水S(h1-h0)g,
所以,m球==ρ水S(h1-h0),
金属球投入水中后沉底,则V球=V排′=S(h2-h0),
所以,ρ球===ρ水;
(2)将该金属球取出放入水中后沉底,金属球受到的浮力:
F浮=ρ水V排′g=ρ水S(h2-h0)g,
则它对容器底的压力:
F=G球-F浮=ρ水S(h1-h0)g-ρ水S(h2-h0)g=ρ水g(h1-h2)S。
12.求证在串联电路中,串联电路的总电阻,等于各导体的电阻之和.
证明:根据流过串联电路各电阻的电流相等和串联电路两端的总电压等于各部分电路两端的电压之和,可得:
I=I1=I2=……=In …………(1)
U=U1+U2+……+Un …………(2)
根据欧姆定律:U=IR,U1=IR1, U2=IR2,…… Un=IRn…………(3)
把上述关系式代入(2)式,整理后可得:R=R1+R2+……+Rn
13.求证在并联电路中,并联电路总电阻的倒数,等于各个导体的电阻倒数之和.
证明:根据并联电路中各支路两端的电压相等和并联电路中的总电流等于各支路电流之和,可得:
U=U1=U2=……=Un ……… (1)
I=I1+I2+……+In …………(2)
由欧姆定律,I=U/R,I1=U1/R1,I2=U2/R2, ……,In=Un/Rn,代入(2)式并考虑到(1)式,得:
1/R=1/R1+1/R2+……1/Rn
同课章节目录
