人教B版 必修4 高一数学 1.2.1三角函数的定义 教学课件(共65张PPT)
文档属性
| 名称 | 人教B版 必修4 高一数学 1.2.1三角函数的定义 教学课件(共65张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 19:02:11 | ||
图片预览







文档简介
(共65张PPT)
新课导入
摩天轮相信同学们都不陌生吧,好多同学都坐过,当你坐上摩天轮后,你就开始绕中心不停地旋转,这样就形成了各种各样的角.
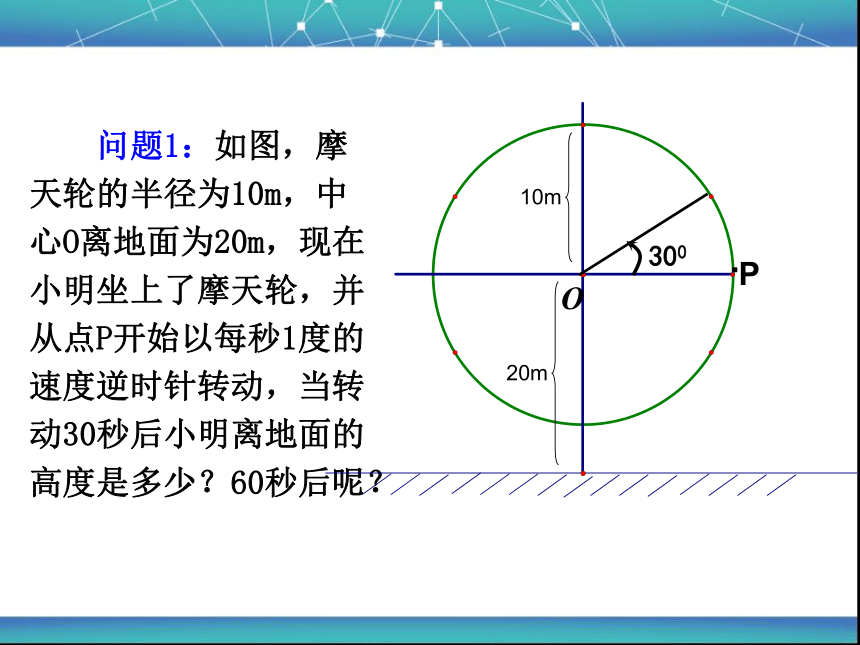
问题1:如图,摩天轮的半径为10m,中心O离地面为20m,现在小明坐上了摩天轮,并从点P开始以每秒1度的速度逆时针转动,当转动30秒后小明离地面的高度是多少?60秒后呢?
.
10m
20m
300
.
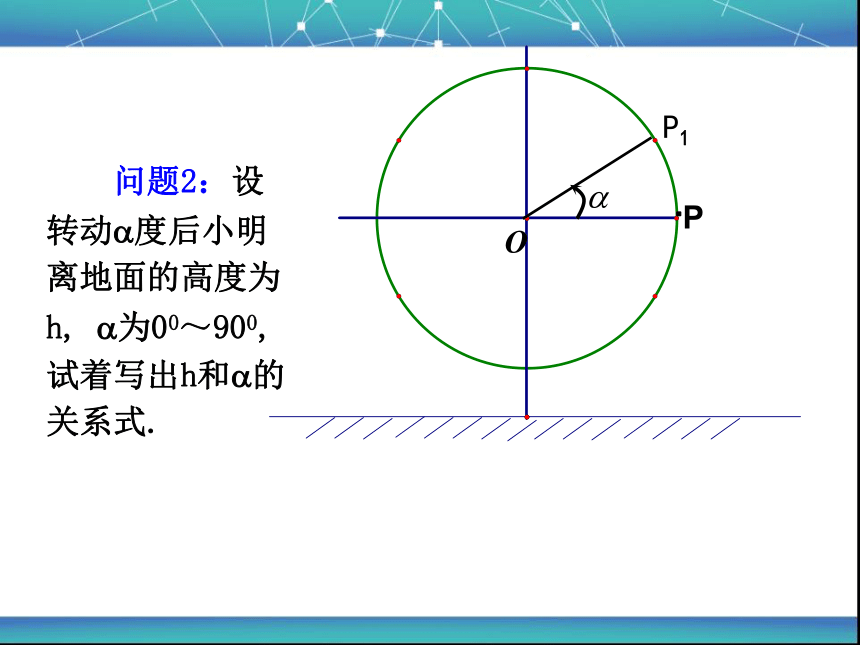
问题2:设转动?度后小明离地面的高度为h, ?为00~900,试着写出h和?的关系式.
P1
1.2.1三角函数的定义
掌握任意角的三角函数的定义;
已知角α终边上一点,会求角α的各三角函数值;
记住三角函数的定义域、值域,诱导公式(一).
教学目标
知识与能力
1、理解并掌握任意角的三角函数的定义;
2、树立映射观点,正确理解三角函数是以实数为自变量的函数;
3、通过对定义域,三角函数值的符号,诱导公式一的推导,提高学生分析、探究、解决问题的能力.
过程与方法
1、使学生认识到事物之间是有联系的,三角函数就是角度(自变量)与比值(函数值)的一种联系方式;
2、学习转化的思想,培养学生严谨治学、一丝不苟的科学精神.
情感态度与价值观
任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号),以及这三种函数的第一组诱导公式.
教学重难点
重点:
用单位圆上点的坐标刻画三角函数,学生熟悉的函数y=f(x)的实数到实数的对应,而这里给出的函数首先是实数(弧度制)到点的坐标的对应,然后才是实数(弧度制)到实数(横坐标或纵坐标)的对应.这就会给学生理解造成一定的困难.
难点:
o
y
x
P(x,y)
?的终边
r
?
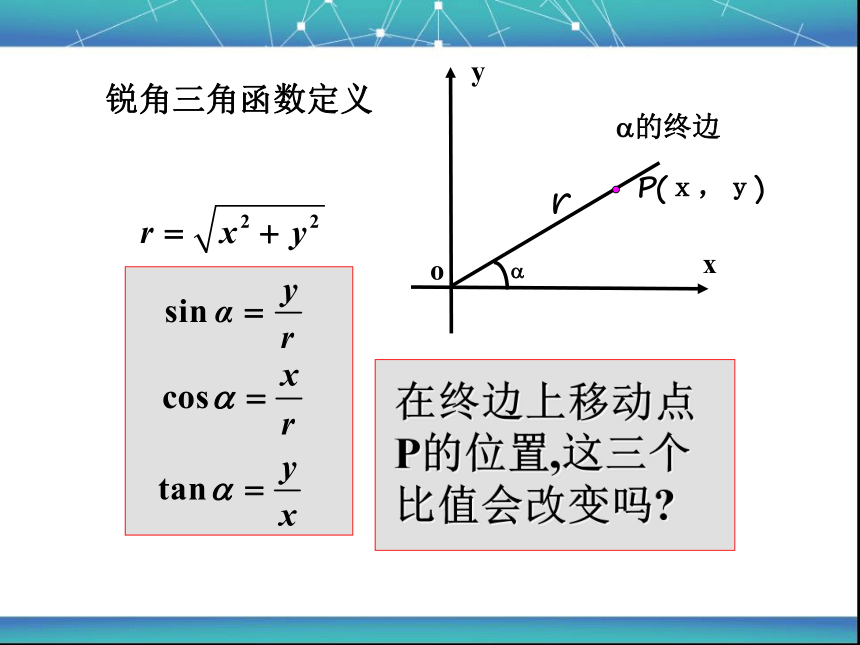
锐角三角函数定义
在终边上移动点P的位置,这三个比值会改变吗?
o
y
x
P(x,y)
?的终边
r=1
?
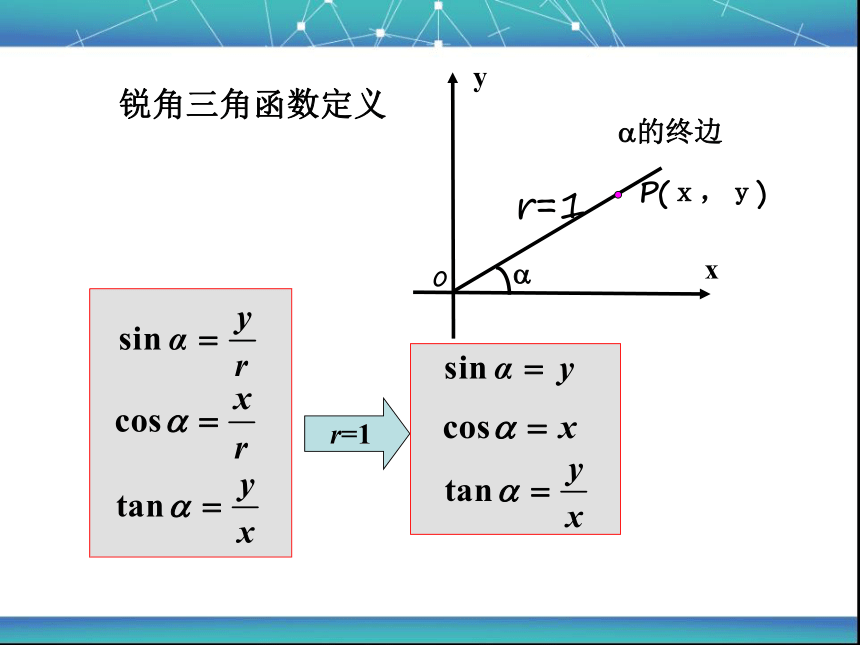
锐角三角函数定义
r=1
P(x,y)
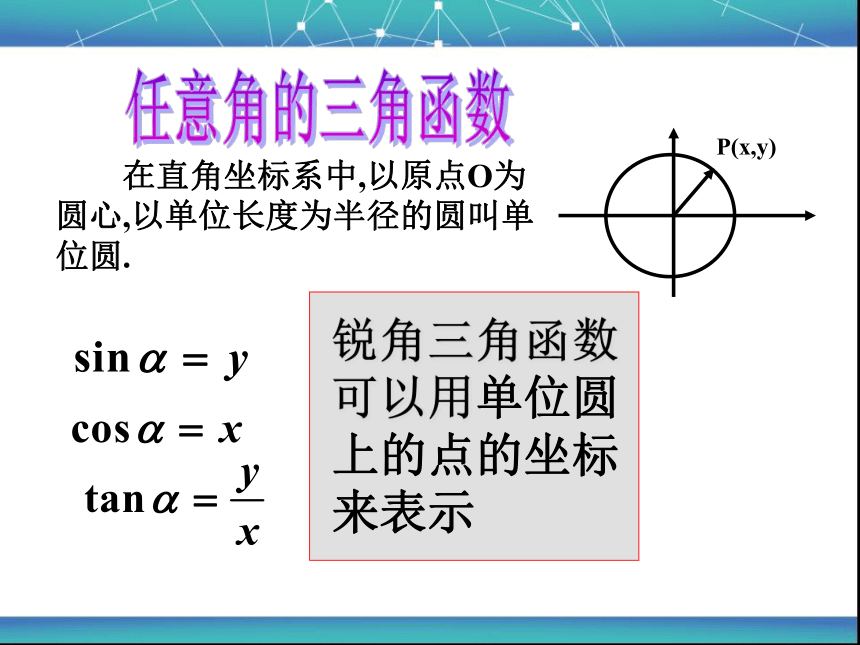
锐角三角函数可以用单位圆上的点的坐标来表示
在直角坐标系中,以原点O为圆心,以单位长度为半径的圆叫单位圆.
任意角的三角函数
推广:
我们也可以利用单位圆定义任意角三角函数(正弦,余弦,正切).
x
y
O
设α是一个任意角,它的终边与单位圆交于点P(x,y)则:
y 叫α的正弦
x叫α的余弦
叫α的正切
任意角的三角函数定义:
对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数,在弧度制中,这三个三角函数的定义域分别是什么?
正、余弦函数的定义域为R,
正切函数的定义域是
思考:
定义域
求α角的三角函数值,即可求α终边与单位圆交于点的纵横坐标或坐标的比值.
如何求α角的三角函数值?
y
x
O
例1:求 的正弦,余弦,正切的值.
根据上述方法否能求得特殊角三角函数值?
角α(角度) 0° 90° 180° 270° 360°
角α(弧度) 0 π/2 π 3π/2 2π
sinα 0 1 0 -1 0
cosα 1 0 -1 0 1
tanα 0 不存在 0 不存在 0
P0(-4,-3)
M0
M
P
y
x
o
分析:由△OMP∽△OM0P0,可求出相应的三角函数值.
例2:已知α的终边经过点P0 (-4,-3),求α角的正弦,余弦,正切的值.
解:
例3:如图所示,已知角a终边上一点P的坐标为(4,-3),求角a的三角函数值.
解:∵ x=4,y=-3
∴
=5
0
y
x
P(4,-3)
a的终边
o
y
x
P(x,y)
?的终边
r
?
事实上: 三角函数也可定义为
设α是一个任意角,它的终边经过点P(x,y),则
根据三角函数的定义能否确定正弦,余弦,正切的值在四个象限内的符号?
任意角的三角函数符号
探究
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
规律:
“一全正、二正弦正、三正切正、四余弦正”.
例4:确定下列三角函数值的符号.
解:
∵
分别位于第三象限、第四象限、第一象限、第四象限.
∴
(1)负 (2)负 (3)正 (4)负
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
+
+
-
-
+
+
-
-
+
+
-
-
例5:
求证:当且仅当不等式组下列不等式组成立时,角θ为第三象限角.
因为sinθ<0,所以θ在第三象限或第四象限,或θ的终边落在y轴的负半轴上.
因为tanθ>0.所以θ在第一象限或第三象限.
由于sinθ<0与tanθ>0同时成立,所以θ在第三象限.
解:?
直角三角中的锐角三角函数
象限角中的锐角三角函数
单位圆上点的坐标表示的锐角三角函数
单位圆上点的坐标表示的任意角三角函数
任意角终边上任一点坐标定义三角函数
反思三角函数的定义
根据三角函数的定义:
终边相同的角的同一三角函数值是否相等?
探究
诱导公式
终边相同
∵终边相同的角的集合为:
点的坐标相同
同一三角函数值
∴
终边相同的角的同一三角函数值相等,由此得到一组公式(公式一):
利用公式一,作用在于可将求任意角的三角函数值,转化为求0~2π (或0°~360°)范围内的三角函数值.
例6:求下列三角函数的值.
解:
前面我们学习了任意角的三角函数,它主要从数上研究了它们,能否从图形上来研究呢?
单位圆中的三角函数线
思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则 ,
都是正数,你能分别用一条线段表示角α的正弦值和余弦值吗?
P(x,y)
O
x
y
M
思考2:若角α为第三象限角,其终边与单位圆的交点为P(x,y),则 ,
都是负数,此时角α的正弦值和余弦值分别用哪条线段表示?
P(x,y)
O
x
y
M
思考3:为了简化上述表示,我们设想将线段的两个端点规定一个为始点,另一个为终点,使得线段具有方向性,带有正负值符号.根据实际需要,应如何规定线段的正方向和负方向?
规定:线段从始点到终点与坐标轴同向时为正方向,反向时为负方向.
α终边
x
y
o
p(x , y)
x
y
o
p(x , y)
α终边
M
M
象OM、MP这种被看作带有方向的线段,叫做有向线段.
一、有向线段
我们规定OM与x轴同向时,OM的方向是正向,x为正值;OM与x轴反向时, OM的方向是负向,x为负值;无论是那种情况都有:OM=x=cosα.
我们规定MP与y轴同向时,MP的方向是正向,y为正值;MP与y轴反向时,MP的方向是负向,y为负值;无论是那种情况都有:MP =y=sinα.
二、正弦线、余弦线
设任意角α与单位圆交于点p(x , y),则r = |op| = 1.
sinα=
y
因此,p(x , y)坐标也表示为p(cosα , sinα).
cosα
= x
x
y
o
p(x , y)
α
x
y
o
x
y
o
x
y
o
x
y
o
α终边
p(x , y)
p
p
p
M
M
M
M
正弦线
余弦线
三、正切线
x
y
o
p
α终边
A
T
称AT为角α的正切线.
过A(1,0)作圆的切线,
x
y
o
x
y
o
x
y
o
x
y
o
M
M
M
M
α终边
p
T
A(1,0)
T
A(1,0)
T
A(1,0)
A(1,0)
T
p
α终边
p
α终边
p
α终边
过A(1,0)作圆的切线
例7:不查表,比较大小.
⑴
解:
x
y
o
1
1
由图形得到
和
解:
由图形得到
x
y
o
1
1
(2)
和
解:
由图形得到
x
y
o
1
⑶
和
1、正弦线
2、余弦线
3、正切线
注意:正弦线、余弦线、正切线都是有向线段,有正负之分.
结论
三角函数线是三角函数的几何表示,它可以直观刻画三角函数的概念与三角函数的定义结合起来,可以从数与形两方面认识三角函数的定义.
定义域为R;
定义域为R;
定义域为
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:
1、任意角的三角函数定义
课堂小结
.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
+
+
-
-
+
+
-
-
+
+
-
-
2、三角函数在象限内的符号
应用
(1)判断符号
(2)求值
3、公式一(诱导公式)
针对性练习
1、 的值为( )
A
A.
B.
C.
D.
解析:
本题主要考察诱导公式:
A. 0
C. 1
D.
B.
2. 则 的值为( )
B
解析:
本题考查同角三角函数的基本关系式和运算能力,以及转化与化归的思想。因
故选B。
3、 若 , 则 等于( )
A. -3
B.
C. 3
D.
D
解析:
故选D
1、以下四个命题中,正确的是( )
D.第四象限的角可表示为:
A.在定义域内,只有终边相同的角的三
角函数值才相等.
B.
C.若a是第二象限的角,则
C
课堂练习
.
2、若角a的终边过点(-3,-2),则( )
A.sina tana>0 B.cosa tana>0
C.sina cosa>0 D.sina cota>0
C
C
C
3
D
B
新课导入
摩天轮相信同学们都不陌生吧,好多同学都坐过,当你坐上摩天轮后,你就开始绕中心不停地旋转,这样就形成了各种各样的角.
问题1:如图,摩天轮的半径为10m,中心O离地面为20m,现在小明坐上了摩天轮,并从点P开始以每秒1度的速度逆时针转动,当转动30秒后小明离地面的高度是多少?60秒后呢?
.
10m
20m
300
.
问题2:设转动?度后小明离地面的高度为h, ?为00~900,试着写出h和?的关系式.
P1
1.2.1三角函数的定义
掌握任意角的三角函数的定义;
已知角α终边上一点,会求角α的各三角函数值;
记住三角函数的定义域、值域,诱导公式(一).
教学目标
知识与能力
1、理解并掌握任意角的三角函数的定义;
2、树立映射观点,正确理解三角函数是以实数为自变量的函数;
3、通过对定义域,三角函数值的符号,诱导公式一的推导,提高学生分析、探究、解决问题的能力.
过程与方法
1、使学生认识到事物之间是有联系的,三角函数就是角度(自变量)与比值(函数值)的一种联系方式;
2、学习转化的思想,培养学生严谨治学、一丝不苟的科学精神.
情感态度与价值观
任意角的正弦、余弦、正切的定义(包括这三种三角函数的定义域和函数值在各象限的符号),以及这三种函数的第一组诱导公式.
教学重难点
重点:
用单位圆上点的坐标刻画三角函数,学生熟悉的函数y=f(x)的实数到实数的对应,而这里给出的函数首先是实数(弧度制)到点的坐标的对应,然后才是实数(弧度制)到实数(横坐标或纵坐标)的对应.这就会给学生理解造成一定的困难.
难点:
o
y
x
P(x,y)
?的终边
r
?
锐角三角函数定义
在终边上移动点P的位置,这三个比值会改变吗?
o
y
x
P(x,y)
?的终边
r=1
?
锐角三角函数定义
r=1
P(x,y)
锐角三角函数可以用单位圆上的点的坐标来表示
在直角坐标系中,以原点O为圆心,以单位长度为半径的圆叫单位圆.
任意角的三角函数
推广:
我们也可以利用单位圆定义任意角三角函数(正弦,余弦,正切).
x
y
O
设α是一个任意角,它的终边与单位圆交于点P(x,y)则:
y 叫α的正弦
x叫α的余弦
叫α的正切
任意角的三角函数定义:
对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数,在弧度制中,这三个三角函数的定义域分别是什么?
正、余弦函数的定义域为R,
正切函数的定义域是
思考:
定义域
求α角的三角函数值,即可求α终边与单位圆交于点的纵横坐标或坐标的比值.
如何求α角的三角函数值?
y
x
O
例1:求 的正弦,余弦,正切的值.
根据上述方法否能求得特殊角三角函数值?
角α(角度) 0° 90° 180° 270° 360°
角α(弧度) 0 π/2 π 3π/2 2π
sinα 0 1 0 -1 0
cosα 1 0 -1 0 1
tanα 0 不存在 0 不存在 0
P0(-4,-3)
M0
M
P
y
x
o
分析:由△OMP∽△OM0P0,可求出相应的三角函数值.
例2:已知α的终边经过点P0 (-4,-3),求α角的正弦,余弦,正切的值.
解:
例3:如图所示,已知角a终边上一点P的坐标为(4,-3),求角a的三角函数值.
解:∵ x=4,y=-3
∴
=5
0
y
x
P(4,-3)
a的终边
o
y
x
P(x,y)
?的终边
r
?
事实上: 三角函数也可定义为
设α是一个任意角,它的终边经过点P(x,y),则
根据三角函数的定义能否确定正弦,余弦,正切的值在四个象限内的符号?
任意角的三角函数符号
探究
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
规律:
“一全正、二正弦正、三正切正、四余弦正”.
例4:确定下列三角函数值的符号.
解:
∵
分别位于第三象限、第四象限、第一象限、第四象限.
∴
(1)负 (2)负 (3)正 (4)负
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
+
+
-
-
+
+
-
-
+
+
-
-
例5:
求证:当且仅当不等式组下列不等式组成立时,角θ为第三象限角.
因为sinθ<0,所以θ在第三象限或第四象限,或θ的终边落在y轴的负半轴上.
因为tanθ>0.所以θ在第一象限或第三象限.
由于sinθ<0与tanθ>0同时成立,所以θ在第三象限.
解:?
直角三角中的锐角三角函数
象限角中的锐角三角函数
单位圆上点的坐标表示的锐角三角函数
单位圆上点的坐标表示的任意角三角函数
任意角终边上任一点坐标定义三角函数
反思三角函数的定义
根据三角函数的定义:
终边相同的角的同一三角函数值是否相等?
探究
诱导公式
终边相同
∵终边相同的角的集合为:
点的坐标相同
同一三角函数值
∴
终边相同的角的同一三角函数值相等,由此得到一组公式(公式一):
利用公式一,作用在于可将求任意角的三角函数值,转化为求0~2π (或0°~360°)范围内的三角函数值.
例6:求下列三角函数的值.
解:
前面我们学习了任意角的三角函数,它主要从数上研究了它们,能否从图形上来研究呢?
单位圆中的三角函数线
思考1:如图,设角α为第一象限角,其终边与单位圆的交点为P(x,y),则 ,
都是正数,你能分别用一条线段表示角α的正弦值和余弦值吗?
P(x,y)
O
x
y
M
思考2:若角α为第三象限角,其终边与单位圆的交点为P(x,y),则 ,
都是负数,此时角α的正弦值和余弦值分别用哪条线段表示?
P(x,y)
O
x
y
M
思考3:为了简化上述表示,我们设想将线段的两个端点规定一个为始点,另一个为终点,使得线段具有方向性,带有正负值符号.根据实际需要,应如何规定线段的正方向和负方向?
规定:线段从始点到终点与坐标轴同向时为正方向,反向时为负方向.
α终边
x
y
o
p(x , y)
x
y
o
p(x , y)
α终边
M
M
象OM、MP这种被看作带有方向的线段,叫做有向线段.
一、有向线段
我们规定OM与x轴同向时,OM的方向是正向,x为正值;OM与x轴反向时, OM的方向是负向,x为负值;无论是那种情况都有:OM=x=cosα.
我们规定MP与y轴同向时,MP的方向是正向,y为正值;MP与y轴反向时,MP的方向是负向,y为负值;无论是那种情况都有:MP =y=sinα.
二、正弦线、余弦线
设任意角α与单位圆交于点p(x , y),则r = |op| = 1.
sinα=
y
因此,p(x , y)坐标也表示为p(cosα , sinα).
cosα
= x
x
y
o
p(x , y)
α
x
y
o
x
y
o
x
y
o
x
y
o
α终边
p(x , y)
p
p
p
M
M
M
M
正弦线
余弦线
三、正切线
x
y
o
p
α终边
A
T
称AT为角α的正切线.
过A(1,0)作圆的切线,
x
y
o
x
y
o
x
y
o
x
y
o
M
M
M
M
α终边
p
T
A(1,0)
T
A(1,0)
T
A(1,0)
A(1,0)
T
p
α终边
p
α终边
p
α终边
过A(1,0)作圆的切线
例7:不查表,比较大小.
⑴
解:
x
y
o
1
1
由图形得到
和
解:
由图形得到
x
y
o
1
1
(2)
和
解:
由图形得到
x
y
o
1
⑶
和
1、正弦线
2、余弦线
3、正切线
注意:正弦线、余弦线、正切线都是有向线段,有正负之分.
结论
三角函数线是三角函数的几何表示,它可以直观刻画三角函数的概念与三角函数的定义结合起来,可以从数与形两方面认识三角函数的定义.
定义域为R;
定义域为R;
定义域为
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:
1、任意角的三角函数定义
课堂小结
.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
+
+
-
-
+
+
-
-
+
+
-
-
2、三角函数在象限内的符号
应用
(1)判断符号
(2)求值
3、公式一(诱导公式)
针对性练习
1、 的值为( )
A
A.
B.
C.
D.
解析:
本题主要考察诱导公式:
A. 0
C. 1
D.
B.
2. 则 的值为( )
B
解析:
本题考查同角三角函数的基本关系式和运算能力,以及转化与化归的思想。因
故选B。
3、 若 , 则 等于( )
A. -3
B.
C. 3
D.
D
解析:
故选D
1、以下四个命题中,正确的是( )
D.第四象限的角可表示为:
A.在定义域内,只有终边相同的角的三
角函数值才相等.
B.
C.若a是第二象限的角,则
C
课堂练习
.
2、若角a的终边过点(-3,-2),则( )
A.sina tana>0 B.cosa tana>0
C.sina cosa>0 D.sina cota>0
C
C
C
3
D
B
