人教B版 必修4 高一数学 1.2.2单位圆与三角函数线 教学课件(共36张PPT)
文档属性
| 名称 | 人教B版 必修4 高一数学 1.2.2单位圆与三角函数线 教学课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 807.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 19:07:49 | ||
图片预览











文档简介
(共36张PPT)
知识回顾
三角函数
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
终边相同的角的同一三角函数的值相等.
假设α是任意一个角,它的终边与单位圆交于点P(x,y) ,那么
(1)y叫做α的正弦(sin α )
记做sin α=y
(2) x叫做α的正弦( cos α )
记做cos α=x
(3) y/x叫做α的正弦(tanα )
记做tanα=y/x(x≠0)
0
x
y
对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的 ,那么,我们再来学习正弦、余弦、正切函数的另一种表示方法——几何表示法
导入新课
1.2.2 单位圆和三角函数线
x
y
o
α
知识与能力
教学目标
单位圆的概念.?
有向线段的概念.?
用正弦线、余弦线、正切线表示任意角的三角函数值.?
过程与方法
理解并掌握单位圆、有向线段的概念.
正确利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值表示出来,即用正弦线、余弦线、正切线表示出来.
通过三角函数的几何表示,使学生进一步加深对数形结合思想的理解,培养良好的思维习惯,拓展思维空间.
情感态度与价值观
教学重难点
重点
正确地用三角函数线表示任意角的三角函数值
难点
正确地用与单位圆有关的三角函数线表示三角函数值
观缆车
观缆车在运动过程中座椅离地面的高度随着转动角度的变化而变化,二者之间是怎样的关系呢?
思考
在观览车轮源面所在的平面内,以观览车轮中心为原点,以水平线为x轴,以转轮半径为单位长建立直角坐标系。设p点为转轮边缘上的一点,他表示座椅的位置,记∠xop为α,则由正弦函数的定义可知
MP=sin α
α
o
M
P
x
y
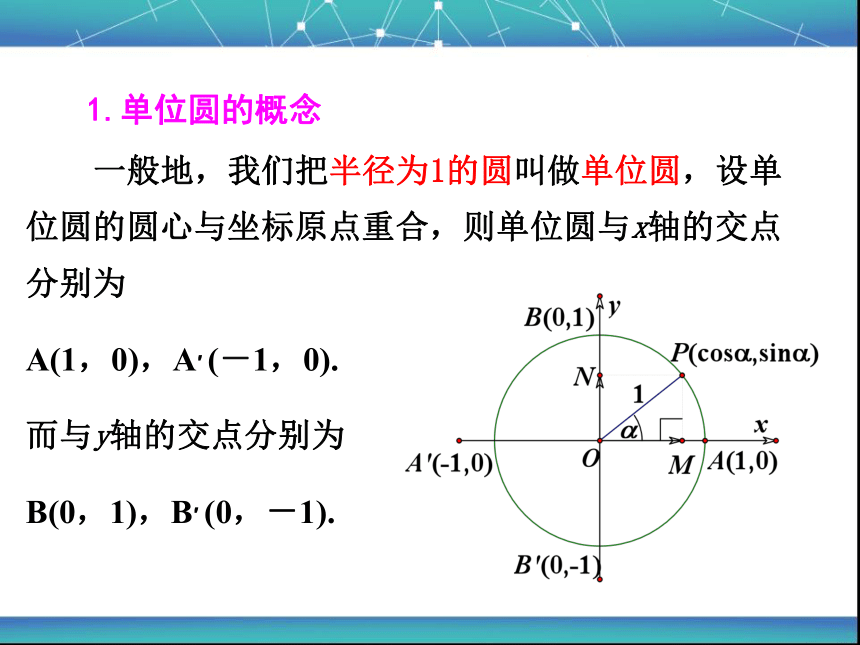
1.单位圆的概念
一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A′ (-1,0).
而与y轴的交点分别为
B(0,1),B′ (0,-1).
2. 有向线段的概念:
带有方向的线段叫有向线段 ,有向线段的数值
由其长度大小和方向来决定。
如在数轴上,|OA|=3,|OB|=3
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
图一
设角α的顶点在圆心O,始边与x轴的正半轴重合,终边与单位圆相交于点P(如图一所示),过点P做PM垂直x轴与M,与作PN垂直y轴于点N,则点M,N分别是点P在x轴、y轴上的正射影(简称射影)。由三角函数的定义可知,点P的坐标为(cos α 、sin α ),即
P (cos α 、sin α )
其中cos α =OM、sin α =ON.
角α的余弦和正弦分别等于角α终边与单位圆交点的横坐标和纵坐标。
结论:
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
下面我们再从图形角度认识一下三角函数。如图所示,角α的终边与单位圆交于点p,过p作x轴的垂线,垂足为M,根据三角函数定义,我们有:
x
y
o
α
p
M
T(1,tan α )
α
A(1,0)
M
x
y
N
o
T
图二
如图所示,以A 为原点建立y′轴与y轴同向,y ′与α的终边相交于点T,则tan α=AT。我们把轴上的向量OM、ON和AT分别叫做α的余弦线、正弦线和正切线。
当角α的终边在x轴上时,点P与点M重合,点T与点A重合,此时,正弦线和正切线都成了一点,他们的数量为零,而余弦线OM=1或-1.
当角α的终边在y轴上时,正弦线MP=1或-1,余弦线变成了一点,它表示的数量为零,正切线不存在。
我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.
分别做出2π/3和-3π/4的正弦线、余弦线和正切线。
例1
解:在执教坐标系中作单位圆如图所示,一ox轴正方向为始边作2π/3的终边与单位圆交于P点,作PM⊥OX轴,垂足为M,由单位圆与ox正方向的交点S作ox轴的垂线与OP的反延长线交于T点,则
sin 2π/3=MP
COS 2π/3=OM
tan 2π/3=AT
A
M
x
y
M′
o
T
T
P′
P
即2π/3的正弦线为MP 、余弦线为OM 、正切线AT。
同理可以作出-3π/4的正弦线、余弦线和正切线。
sin -3π/4 =M′P′
COS -3π/4 =OM ′
tan -3π/4 =AT ′
即-3π/4的正弦线为M′P′
余弦线为 OM ′
正切线为 AT ′
A
M
x
y
M′
o
T
T
P′
P
例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.
解:由三角函数线得
sin1cos1>cos1.5
tan2例3. 已知sinx=0.5,求角x的大小.(0?解:由在y轴上找到y=0.5的点,做x轴的平行线,交单位圆于点P和P’两点,由三角函数线知
x1=30?, x2=150?.
角α=x,且0思考与讨论
1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。
课堂小结
2. 三角函数线的位置 :
正弦线为从原点到α的终边与单位圆的交点在y轴上的射影的有向线段;
正切线在过单位圆与x轴正方向的交点的切线上,为有向线段
余弦线为从原点到α的终边与单位圆的交点在x轴上的射影的有向线段;
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
3. 特殊情况:
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。
1. 利用三角函数线证明|sinα|+|cosα|≥1.
证明:在△OMP中,OP=1,OM=|cosα|, MP=ON=|sinα|,
因为三角形两边之和大于第三边,所以
|sinα|+|cosα|≥1。
课堂练习
2. 已知α∈(0, ),试证明sinα<α证明:sinα=|ON|=|MP|,
α =
tanα=|AT|.
又
所以
即sinα<α3、根据下列三角函数值,求作角a的终边,然后求角的取值集合
???(1)sinα=1/2;???????(2)cosα=1/2
(3)tanα=-1????????(4)sinα>1/2.
分析:(1)已知角α的正弦值,可知MP=1/2,则P点的纵坐标为1/2.所以在y轴上取点(0,1/2),过这点作x轴的平行线,交单位圆于P1,P2两点,则OP1,OP2是角α的终边,因而角a的取值集合为{α|α=2kπ+π/6,或α=2kπ+π/6 π,k∈Z}
(1)
(2)
(2)因为OM=1/2,则在x轴上取点(1/2,0),过该点作x轴的垂线,交单位圆于P1,P2两点,OP1,OP2是所求角χ的终边,α的取值集合为{α|α=2kπ±π/3,k∈Z}.
(3)在单位圆过点A(1,0)的切线上取AT=-1连续OT,OT所在直线与单位圆交于P1,P2两点,OP1、OP2是角a的终边,则角a的取值集合是{α|α=2kπ+3π/4,或α=2kπ+7/4π,k∈Z}={α|α=kπ±3/4π,k∈Z}
(3)
(4)
(4)这是一个三角不等式,所求的不是一个确定的角,而是适合条件的角的范围.如图4,作出正弦值等于1/2的角χ的终边,正弦值大于1/2的角的终边与单位圆的交点在劣弧P1P2上,所以所求角的范围如图7中的阴影部分,α的取值集合是{χ|2kπ+π/6<χ<2kπ+5/6π,k∈Z}
知识回顾
三角函数
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
终边相同的角的同一三角函数的值相等.
假设α是任意一个角,它的终边与单位圆交于点P(x,y) ,那么
(1)y叫做α的正弦(sin α )
记做sin α=y
(2) x叫做α的正弦( cos α )
记做cos α=x
(3) y/x叫做α的正弦(tanα )
记做tanα=y/x(x≠0)
0
x
y
对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的 ,那么,我们再来学习正弦、余弦、正切函数的另一种表示方法——几何表示法
导入新课
1.2.2 单位圆和三角函数线
x
y
o
α
知识与能力
教学目标
单位圆的概念.?
有向线段的概念.?
用正弦线、余弦线、正切线表示任意角的三角函数值.?
过程与方法
理解并掌握单位圆、有向线段的概念.
正确利用与单位圆有关的有向线段,将任意角α的正弦、余弦、正切函数值表示出来,即用正弦线、余弦线、正切线表示出来.
通过三角函数的几何表示,使学生进一步加深对数形结合思想的理解,培养良好的思维习惯,拓展思维空间.
情感态度与价值观
教学重难点
重点
正确地用三角函数线表示任意角的三角函数值
难点
正确地用与单位圆有关的三角函数线表示三角函数值
观缆车
观缆车在运动过程中座椅离地面的高度随着转动角度的变化而变化,二者之间是怎样的关系呢?
思考
在观览车轮源面所在的平面内,以观览车轮中心为原点,以水平线为x轴,以转轮半径为单位长建立直角坐标系。设p点为转轮边缘上的一点,他表示座椅的位置,记∠xop为α,则由正弦函数的定义可知
MP=sin α
α
o
M
P
x
y
1.单位圆的概念
一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A′ (-1,0).
而与y轴的交点分别为
B(0,1),B′ (0,-1).
2. 有向线段的概念:
带有方向的线段叫有向线段 ,有向线段的数值
由其长度大小和方向来决定。
如在数轴上,|OA|=3,|OB|=3
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
图一
设角α的顶点在圆心O,始边与x轴的正半轴重合,终边与单位圆相交于点P(如图一所示),过点P做PM垂直x轴与M,与作PN垂直y轴于点N,则点M,N分别是点P在x轴、y轴上的正射影(简称射影)。由三角函数的定义可知,点P的坐标为(cos α 、sin α ),即
P (cos α 、sin α )
其中cos α =OM、sin α =ON.
角α的余弦和正弦分别等于角α终边与单位圆交点的横坐标和纵坐标。
结论:
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
下面我们再从图形角度认识一下三角函数。如图所示,角α的终边与单位圆交于点p,过p作x轴的垂线,垂足为M,根据三角函数定义,我们有:
x
y
o
α
p
M
T(1,tan α )
α
A(1,0)
M
x
y
N
o
T
图二
如图所示,以A 为原点建立y′轴与y轴同向,y ′与α的终边相交于点T,则tan α=AT。我们把轴上的向量OM、ON和AT分别叫做α的余弦线、正弦线和正切线。
当角α的终边在x轴上时,点P与点M重合,点T与点A重合,此时,正弦线和正切线都成了一点,他们的数量为零,而余弦线OM=1或-1.
当角α的终边在y轴上时,正弦线MP=1或-1,余弦线变成了一点,它表示的数量为零,正切线不存在。
我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.
分别做出2π/3和-3π/4的正弦线、余弦线和正切线。
例1
解:在执教坐标系中作单位圆如图所示,一ox轴正方向为始边作2π/3的终边与单位圆交于P点,作PM⊥OX轴,垂足为M,由单位圆与ox正方向的交点S作ox轴的垂线与OP的反延长线交于T点,则
sin 2π/3=MP
COS 2π/3=OM
tan 2π/3=AT
A
M
x
y
M′
o
T
T
P′
P
即2π/3的正弦线为MP 、余弦线为OM 、正切线AT。
同理可以作出-3π/4的正弦线、余弦线和正切线。
sin -3π/4 =M′P′
COS -3π/4 =OM ′
tan -3π/4 =AT ′
即-3π/4的正弦线为M′P′
余弦线为 OM ′
正切线为 AT ′
A
M
x
y
M′
o
T
T
P′
P
例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.
解:由三角函数线得
sin1
tan2
x1=30?, x2=150?.
角α=x,且0
1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。
课堂小结
2. 三角函数线的位置 :
正弦线为从原点到α的终边与单位圆的交点在y轴上的射影的有向线段;
正切线在过单位圆与x轴正方向的交点的切线上,为有向线段
余弦线为从原点到α的终边与单位圆的交点在x轴上的射影的有向线段;
α
P(cos α ,sin α )
A(1,0)
M
B (0、1)
A ′ (-1、0)
B′ ( 0、-1 )
x
y
N
o
3. 特殊情况:
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。
1. 利用三角函数线证明|sinα|+|cosα|≥1.
证明:在△OMP中,OP=1,OM=|cosα|, MP=ON=|sinα|,
因为三角形两边之和大于第三边,所以
|sinα|+|cosα|≥1。
课堂练习
2. 已知α∈(0, ),试证明sinα<α
α =
tanα=|AT|.
又
所以
即sinα<α
???(1)sinα=1/2;???????(2)cosα=1/2
(3)tanα=-1????????(4)sinα>1/2.
分析:(1)已知角α的正弦值,可知MP=1/2,则P点的纵坐标为1/2.所以在y轴上取点(0,1/2),过这点作x轴的平行线,交单位圆于P1,P2两点,则OP1,OP2是角α的终边,因而角a的取值集合为{α|α=2kπ+π/6,或α=2kπ+π/6 π,k∈Z}
(1)
(2)
(2)因为OM=1/2,则在x轴上取点(1/2,0),过该点作x轴的垂线,交单位圆于P1,P2两点,OP1,OP2是所求角χ的终边,α的取值集合为{α|α=2kπ±π/3,k∈Z}.
(3)在单位圆过点A(1,0)的切线上取AT=-1连续OT,OT所在直线与单位圆交于P1,P2两点,OP1、OP2是角a的终边,则角a的取值集合是{α|α=2kπ+3π/4,或α=2kπ+7/4π,k∈Z}={α|α=kπ±3/4π,k∈Z}
(3)
(4)
(4)这是一个三角不等式,所求的不是一个确定的角,而是适合条件的角的范围.如图4,作出正弦值等于1/2的角χ的终边,正弦值大于1/2的角的终边与单位圆的交点在劣弧P1P2上,所以所求角的范围如图7中的阴影部分,α的取值集合是{χ|2kπ+π/6<χ<2kπ+5/6π,k∈Z}
