人教B版 必修4 高一数学 1.2.3同角三角函数的基本关系式 教学课件(共38张PPT)
文档属性
| 名称 | 人教B版 必修4 高一数学 1.2.3同角三角函数的基本关系式 教学课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 841.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 19:05:39 | ||
图片预览











文档简介
(共38张PPT)
问题1:回顾三角函数的定义.
设置目的:温故知新,三角函数定义是推导关系式的基础理论.
知识回顾
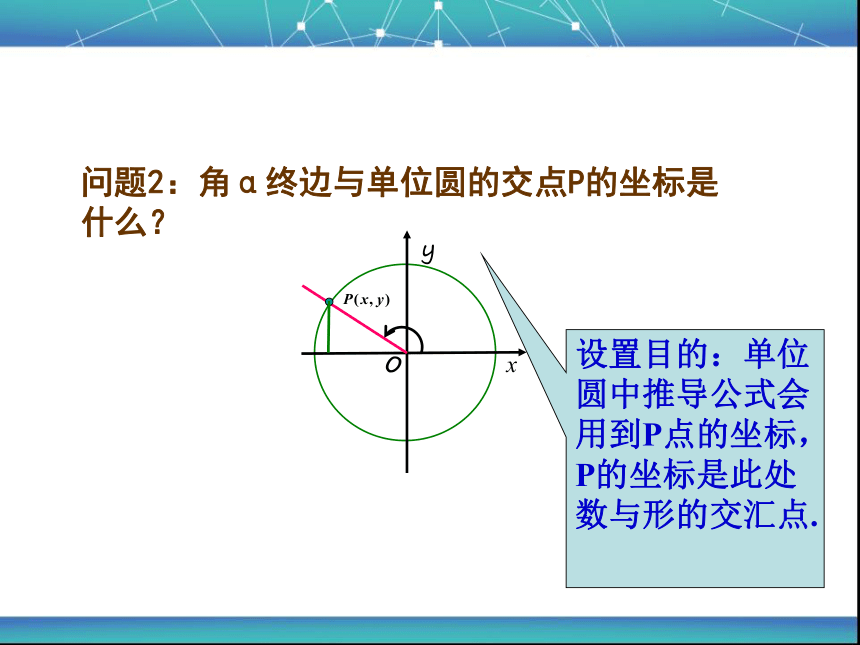
问题2:角α终边与单位圆的交点P的坐标是什么?
x
y
O
设置目的:单位圆中推导公式会用到P点的坐标,P的坐标是此处数与形的交汇点.
1.2.3 同角三角函数的基本关系
教学目标
让学生掌握公式的推导过程,熟记基本关系式的内容,明确基本关系式在三个方面的应用:
(1)知道一个角的一个三角函数值能求这个角的其他三角函数值;
(2)化简三角函数式;
(3)证明三角恒等式.
知识与能力
培养学生由特殊结论-----猜想一般规律-----进行严格证明的科学思维方式;通过用单位圆推导公式培养学生用数形结合思想处理数学问题的能力;通过求值、化简、证明培养学生逻辑推理能力;通过例题与练习提高学生动手能力和分析解决问题的能力.
过程与方法
培养学生积极参与大胆探索的精神;让学生通过自主学习体验学习的成就感,培养学生学习数学的兴趣和信心.
情感态度与价值观
同角三角函数基本关系式推导及应用.
知识技能线
情感态度线
过程方法线
观察分析
特殊到一般
灵活运用能力及应用意识
创设情景引入课题
公式推导
公式运用
探究尝试
数形结合
灵活运用
化归、方程思想
突重点
观察能力
合作交流,归纳猜想能力
抓三线、
教学重难点
重点:
关系式在解题中的灵活选取,及使用公式时由函数值正负号的选取而导致的角的范围的讨论.
抓两点、破难点
情感、思维的兴奋点
知识层层深入
难点:
由三角函数定义我们可以看到:
弦与弦
当 时,
即
有意义时,有:
弦与切
同角三角函数的基本关系:
结论
用文字叙述:
同一个角α的正弦、余弦的平方和等于1,商等于角α的正切;同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数).
为了加深对关系式的认识,在公式给出后设置了几点注意 :
1、同角的理解:
2、对“任意”一个角(在使函数有意义的前提下)关系式都成立.
3、 是 的简写形式,与 不同.
4、公式可以变形使用
已知 ,且 是第二象限角,
求 , 的值.
解:
从而 .
例1:
因为sinα2+cosα2=1,所以
25
9
)
5
4
(
1
sin
1
cos
2
2
2
=
-
=
-
=
a
a
又因为角 是第二象限角,所以
.
0
cos
<
a
a
.
5
3
25
9
cos
-
=
-
=
\
a
3
4
)
5
3
(
5
4
cos
sin
tan
-
=
-
=
=
a
a
a
已知 ,求 的值.
解:
为什么?
例2:
,
1
cos
,
0
cos
-
?
<
a
a
且
因为
所以 是第二或第三象限角.
如果 是第二象限角,那么
a
a
,
17
15
)
17
8
(
1
cos
1
sin
2
=
-
-
=
-
a
a
.
8
15
)
8
17
(
17
15
cos
sin
tan
-
=
-
=
=
a
a
a
如果 是第三象限角,那么
a
,
17
15
sin
-
a
.
8
15
tan
=
a
1、已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.
2、解题时产生遗漏的主要原因是:①没有确定好或不去确定角的终边位置;②利用平方关系开平方时,漏掉了负的平方根.
总结
求证:
例3
证法1:
由
知
所以
于是
所以原式成立.
且
所以原式成立.
证法2:
因为
总结:对于例3这类题,由结论,交叉相乘,得: ,即: ,所以,可以由同角的正弦、余弦的平方和为1这个关系式入手来证明.另外,也可以采用“分母有理化”形式的方法来证明,原式左边的分子与分母同乘以(1+sinx).
解:
已知
,求
例4:
因此 , …….
1、同角三角函数的三组关系式的前提是“同角”,
2、诸如 , ,……它们都是
条件等式,即它们成立的前提是表达式有意义.
课堂小结
3、利用平方关系时,往往要开方,因此要先
根据角所在象限确定符号,即要就角所在
象限进行分类讨论.
针对性练习
1、 若 ,则 的值为( )
D.
A.
B.
C.
C
解析:
有已知得:
∴
2、已知 ,则
( )
D.
A.
B.
C.
D
解析:
本题考查同角三角函数关系及求值问题
所求式
3、 已知sinα= 则sin4α-cos4α的值为( )
B.
C. D.
A
解析:
sin4α-cos4α=sin2α-cos2α=2sin2α-1=
1、
,则
的值等于( )
A.
B.
C.
D.
B
课堂练习
2、已知 ,则cosα-sinα的值等于 ( )
A.
B.
D.
C.
B
3、若
,则
的值为________________.
4、已知
则m=_________;
__________.
0或8
,
已知 ,求
∵
∴
又∵
∴α在第二或三象限角.
解:
5、
α在第二象限时,即有
从而
当
α在第四象限时,即有
从而
当
∴
∴
已知
并且α是第二象限角,
求
∵
∴
又∵
α是第二象限角,
即有
从而
∴
解:
6、
,
,
7、已知
,求
的值.
由
可得:
解:
于是:
∴
问题1:回顾三角函数的定义.
设置目的:温故知新,三角函数定义是推导关系式的基础理论.
知识回顾
问题2:角α终边与单位圆的交点P的坐标是什么?
x
y
O
设置目的:单位圆中推导公式会用到P点的坐标,P的坐标是此处数与形的交汇点.
1.2.3 同角三角函数的基本关系
教学目标
让学生掌握公式的推导过程,熟记基本关系式的内容,明确基本关系式在三个方面的应用:
(1)知道一个角的一个三角函数值能求这个角的其他三角函数值;
(2)化简三角函数式;
(3)证明三角恒等式.
知识与能力
培养学生由特殊结论-----猜想一般规律-----进行严格证明的科学思维方式;通过用单位圆推导公式培养学生用数形结合思想处理数学问题的能力;通过求值、化简、证明培养学生逻辑推理能力;通过例题与练习提高学生动手能力和分析解决问题的能力.
过程与方法
培养学生积极参与大胆探索的精神;让学生通过自主学习体验学习的成就感,培养学生学习数学的兴趣和信心.
情感态度与价值观
同角三角函数基本关系式推导及应用.
知识技能线
情感态度线
过程方法线
观察分析
特殊到一般
灵活运用能力及应用意识
创设情景引入课题
公式推导
公式运用
探究尝试
数形结合
灵活运用
化归、方程思想
突重点
观察能力
合作交流,归纳猜想能力
抓三线、
教学重难点
重点:
关系式在解题中的灵活选取,及使用公式时由函数值正负号的选取而导致的角的范围的讨论.
抓两点、破难点
情感、思维的兴奋点
知识层层深入
难点:
由三角函数定义我们可以看到:
弦与弦
当 时,
即
有意义时,有:
弦与切
同角三角函数的基本关系:
结论
用文字叙述:
同一个角α的正弦、余弦的平方和等于1,商等于角α的正切;同一个角的正切、余切之积等于1(即同一个角的正切、余切互为倒数).
为了加深对关系式的认识,在公式给出后设置了几点注意 :
1、同角的理解:
2、对“任意”一个角(在使函数有意义的前提下)关系式都成立.
3、 是 的简写形式,与 不同.
4、公式可以变形使用
已知 ,且 是第二象限角,
求 , 的值.
解:
从而 .
例1:
因为sinα2+cosα2=1,所以
25
9
)
5
4
(
1
sin
1
cos
2
2
2
=
-
=
-
=
a
a
又因为角 是第二象限角,所以
.
0
cos
<
a
a
.
5
3
25
9
cos
-
=
-
=
\
a
3
4
)
5
3
(
5
4
cos
sin
tan
-
=
-
=
=
a
a
a
已知 ,求 的值.
解:
为什么?
例2:
,
1
cos
,
0
cos
-
?
<
a
a
且
因为
所以 是第二或第三象限角.
如果 是第二象限角,那么
a
a
,
17
15
)
17
8
(
1
cos
1
sin
2
=
-
-
=
-
a
a
.
8
15
)
8
17
(
17
15
cos
sin
tan
-
=
-
=
=
a
a
a
如果 是第三象限角,那么
a
,
17
15
sin
-
a
.
8
15
tan
=
a
1、已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.
2、解题时产生遗漏的主要原因是:①没有确定好或不去确定角的终边位置;②利用平方关系开平方时,漏掉了负的平方根.
总结
求证:
例3
证法1:
由
知
所以
于是
所以原式成立.
且
所以原式成立.
证法2:
因为
总结:对于例3这类题,由结论,交叉相乘,得: ,即: ,所以,可以由同角的正弦、余弦的平方和为1这个关系式入手来证明.另外,也可以采用“分母有理化”形式的方法来证明,原式左边的分子与分母同乘以(1+sinx).
解:
已知
,求
例4:
因此 , …….
1、同角三角函数的三组关系式的前提是“同角”,
2、诸如 , ,……它们都是
条件等式,即它们成立的前提是表达式有意义.
课堂小结
3、利用平方关系时,往往要开方,因此要先
根据角所在象限确定符号,即要就角所在
象限进行分类讨论.
针对性练习
1、 若 ,则 的值为( )
D.
A.
B.
C.
C
解析:
有已知得:
∴
2、已知 ,则
( )
D.
A.
B.
C.
D
解析:
本题考查同角三角函数关系及求值问题
所求式
3、 已知sinα= 则sin4α-cos4α的值为( )
B.
C. D.
A
解析:
sin4α-cos4α=sin2α-cos2α=2sin2α-1=
1、
,则
的值等于( )
A.
B.
C.
D.
B
课堂练习
2、已知 ,则cosα-sinα的值等于 ( )
A.
B.
D.
C.
B
3、若
,则
的值为________________.
4、已知
则m=_________;
__________.
0或8
,
已知 ,求
∵
∴
又∵
∴α在第二或三象限角.
解:
5、
α在第二象限时,即有
从而
当
α在第四象限时,即有
从而
当
∴
∴
已知
并且α是第二象限角,
求
∵
∴
又∵
α是第二象限角,
即有
从而
∴
解:
6、
,
,
7、已知
,求
的值.
由
可得:
解:
于是:
∴
