人教B版高中数学 必修4 第二章 2.1.4数乘向量 同步教学课件(共40张PPT)
文档属性
| 名称 | 人教B版高中数学 必修4 第二章 2.1.4数乘向量 同步教学课件(共40张PPT) | 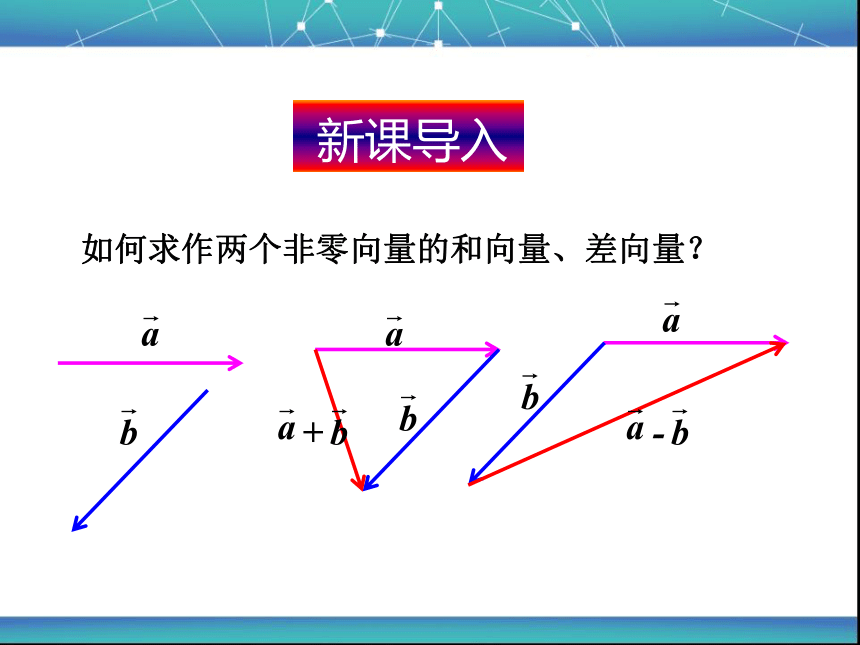 | |
| 格式 | zip | ||
| 文件大小 | 780.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 19:04:21 | ||
图片预览












文档简介
(共40张PPT)
如何求作两个非零向量的和向量、差向量?
新课导入
问题提出
相同的几个数相加可以转化为数乘运算,如3+3+3+3+3=5×3=15.那么相等的几个向量相加是否也能转化为数乘运算呢?这需要从理论上进行探究.
2.1.4 数乘向量
O
A
B
C
P
Q
M
N
掌握实数与向量的积的定义及其几何意义;理解实数与向量的积的运算律,并能运用运算律进行化简;理解向量共线的条件,并能判断三点共线.
教学目标
过程与方法
培养学生的转化思想.
知识与能力
情感态度与价值观
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
教学重点:
教学难点:
向量共线的条件.
向量数乘运算的意义及运算律,向量共线的条件.
教学重难点
思考:已知非零向量 ,作出 和 ,你能说明它们的几何意义吗?
O
A
B
C
P
Q
M
N
实数 与向量 的积是一个向量,这种运算叫做向量的数乘.
向量的数乘的定义:
记作:
当 时, 的方向与 的方向相反;
特别地,当 时,
(2)当 时, 的方向与 的方向相同;
它的长度和方向规定如下:
数乘向量的运算律:
结合律
第一分配律
第二分配律
一般地:
=
一般地:
一般地:
特别地,我们有
例1.计算:
(1)
(2)
(3)
解:
向量 与非零向量 共线的充分必要条件是有且仅有一个实数 ,使 .
定理
综上,如果 与 共线,那么有且只有一个实数 使
证明:(1)对于向量 ,如果有一个实数 使 那么,由向量数乘的定义知, 与 共线.
(2)已知 与 共线, ,且向量 的长度是向量 的 倍,即 ,那么当 同向时,有 ;当 反向时,有
例2:如图:已知 , ,试判断
与 是否共线.
A
B
D
E
C
∴ 与 共线.
解:
例3:如图,已知任意两个向量 ,试作
你能判断A、B、C三点之间的位置关系吗?为什么?
A
B
C
O
例4:如图, 的两条对角线相交于点M,且 ,你能用 、 来表示 .
A
B
D
C
M
B
A
D
M
C
B
A
D
M
C
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
2、若 ,则可能有λ=0,也可能有
.
课堂小结
3、向量的数乘运算律,不是规定,而是可以证明的结论.向量共线定理是平面几何中证明三点共线,直线平行,线段数量关系的理论依据.
针对练习
1、对于向量a、b、c和实数λ,下列命题中真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
B
解析:
时也有a·b=0,故A不正确;
由a2=b2,只能得到 ,所以C不正确;
由a·b=a·c得不到b=c,如a为零向量或a与b、c垂直时,故选B。
2、已知向量a与向量b的夹角为120°,且 ,那么a·b的值为_________。
-8
解析:
3、在平行四边形OABC的对角线OB的两端点分别为O(0,0),B(1,1),则 __________
1
解析:
∴
由题意知A(1,0),C(0,1),
1、若 则化简
2、已知 是不共线向量,
则 与 共线的充要条件是实数
课堂练习
3、给出下列命题:
(1)
存在唯一的实数λ ,使
(2)
存在不全为零的实数 使
(3)
若存在实数 使
(3)
不存在实数 使
其中是真命题的是 ( )
B
A、①和 B、②和③ C、①和② D、③和④
4、如图,在平行四边形ABCD中,点M是AB中点,点N在线段BD上,且有 BN= BD,求证:M、N、C三点共线.
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
证明:
设
由已知得
∴
而
∴
M、N、C三点共线.
∴
5、设 是两个不共线的向量,
,若A,B,C三点共线,求k的值.
解:
若A,B,D三点共线,则
共线,
,即
由于
可得:
故
如何求作两个非零向量的和向量、差向量?
新课导入
问题提出
相同的几个数相加可以转化为数乘运算,如3+3+3+3+3=5×3=15.那么相等的几个向量相加是否也能转化为数乘运算呢?这需要从理论上进行探究.
2.1.4 数乘向量
O
A
B
C
P
Q
M
N
掌握实数与向量的积的定义及其几何意义;理解实数与向量的积的运算律,并能运用运算律进行化简;理解向量共线的条件,并能判断三点共线.
教学目标
过程与方法
培养学生的转化思想.
知识与能力
情感态度与价值观
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
教学重点:
教学难点:
向量共线的条件.
向量数乘运算的意义及运算律,向量共线的条件.
教学重难点
思考:已知非零向量 ,作出 和 ,你能说明它们的几何意义吗?
O
A
B
C
P
Q
M
N
实数 与向量 的积是一个向量,这种运算叫做向量的数乘.
向量的数乘的定义:
记作:
当 时, 的方向与 的方向相反;
特别地,当 时,
(2)当 时, 的方向与 的方向相同;
它的长度和方向规定如下:
数乘向量的运算律:
结合律
第一分配律
第二分配律
一般地:
=
一般地:
一般地:
特别地,我们有
例1.计算:
(1)
(2)
(3)
解:
向量 与非零向量 共线的充分必要条件是有且仅有一个实数 ,使 .
定理
综上,如果 与 共线,那么有且只有一个实数 使
证明:(1)对于向量 ,如果有一个实数 使 那么,由向量数乘的定义知, 与 共线.
(2)已知 与 共线, ,且向量 的长度是向量 的 倍,即 ,那么当 同向时,有 ;当 反向时,有
例2:如图:已知 , ,试判断
与 是否共线.
A
B
D
E
C
∴ 与 共线.
解:
例3:如图,已知任意两个向量 ,试作
你能判断A、B、C三点之间的位置关系吗?为什么?
A
B
C
O
例4:如图, 的两条对角线相交于点M,且 ,你能用 、 来表示 .
A
B
D
C
M
B
A
D
M
C
B
A
D
M
C
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
2、若 ,则可能有λ=0,也可能有
.
课堂小结
3、向量的数乘运算律,不是规定,而是可以证明的结论.向量共线定理是平面几何中证明三点共线,直线平行,线段数量关系的理论依据.
针对练习
1、对于向量a、b、c和实数λ,下列命题中真命题是( )
A.若a·b=0,则a=0或b=0
B.若λa=0,则λ=0或a=0
C.若a2=b2,则a=b或a=-b
D.若a·b=a·c,则b=c
B
解析:
时也有a·b=0,故A不正确;
由a2=b2,只能得到 ,所以C不正确;
由a·b=a·c得不到b=c,如a为零向量或a与b、c垂直时,故选B。
2、已知向量a与向量b的夹角为120°,且 ,那么a·b的值为_________。
-8
解析:
3、在平行四边形OABC的对角线OB的两端点分别为O(0,0),B(1,1),则 __________
1
解析:
∴
由题意知A(1,0),C(0,1),
1、若 则化简
2、已知 是不共线向量,
则 与 共线的充要条件是实数
课堂练习
3、给出下列命题:
(1)
存在唯一的实数λ ,使
(2)
存在不全为零的实数 使
(3)
若存在实数 使
(3)
不存在实数 使
其中是真命题的是 ( )
B
A、①和 B、②和③ C、①和② D、③和④
4、如图,在平行四边形ABCD中,点M是AB中点,点N在线段BD上,且有 BN= BD,求证:M、N、C三点共线.
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
证明:
设
由已知得
∴
而
∴
M、N、C三点共线.
∴
5、设 是两个不共线的向量,
,若A,B,C三点共线,求k的值.
解:
若A,B,D三点共线,则
共线,
,即
由于
可得:
故
