人教B版高中数学 必修4 第二章 2.1.2向量的加法 同步教学课件(共33张PPT)
文档属性
| 名称 | 人教B版高中数学 必修4 第二章 2.1.2向量的加法 同步教学课件(共33张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 19:06:52 | ||
图片预览







文档简介
(共33张PPT)
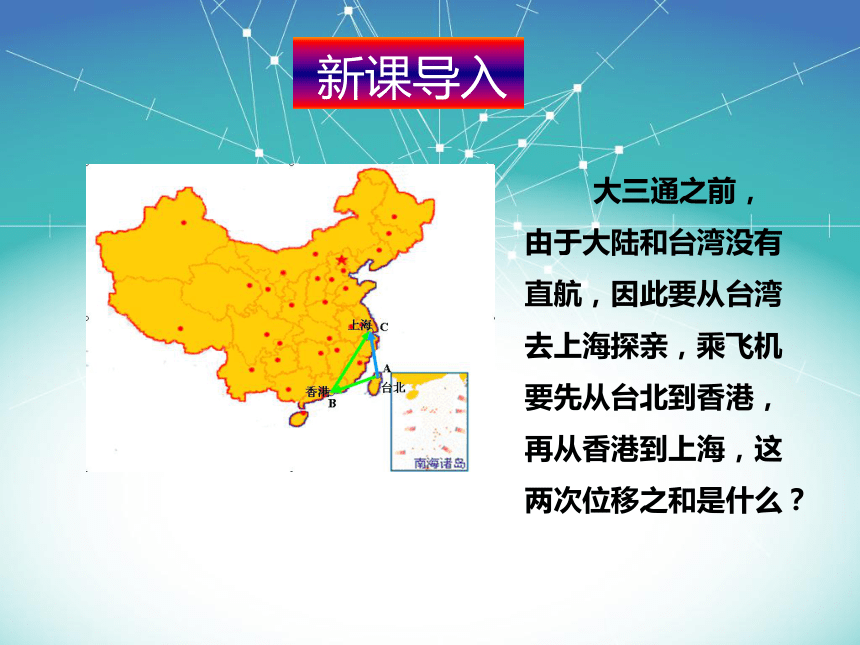
相等向量与相反向量
单位向量与零向量
向 量
向量的大小
(长度、模)
向量的方向
有向线段
平行向量(共线向量)
既有大小又有方向的量叫向量;
向量不能比较大小,但向量的模可以比较大小.
知识回顾
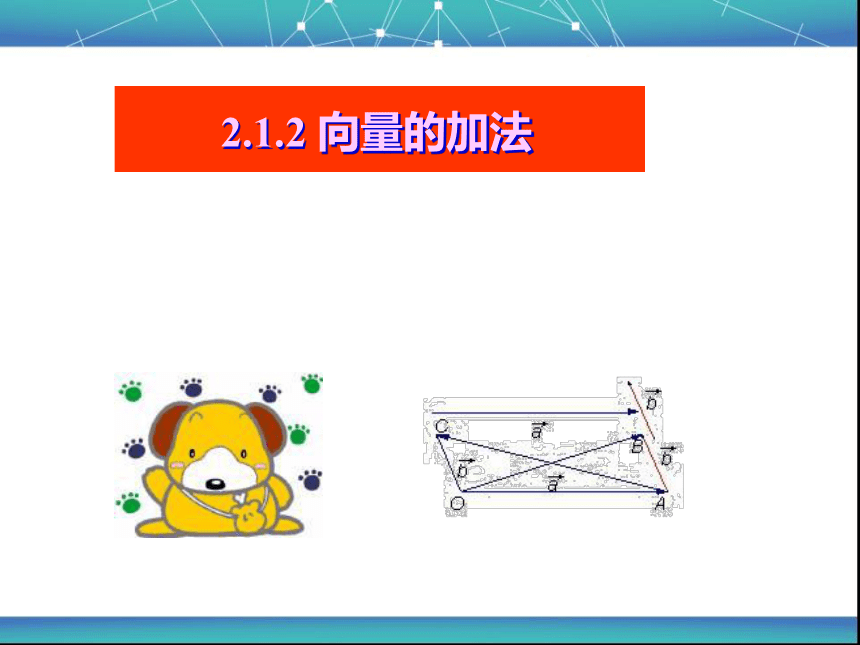
大三通之前,由于大陆和台湾没有直航,因此要从台湾去上海探亲,乘飞机要先从台北到香港,再从香港到上海,这两次位移之和是什么?
新课导入
2.1.2 向量的加法
知识与能力
理解向量的和,掌握向量加法的三角形法则和平行四边形法则,向量加法的运算律.
过程与方法
情感态度与价值观
提高学生观察、归纳、迁移能力和动手能;培养学生的转化思想.
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
教学目标
重点:
难点:
向量加法的三角形法则和平行四边形法则,向量加法的运算律.
对向量和的理解.
教学重难点
E
O
O
E
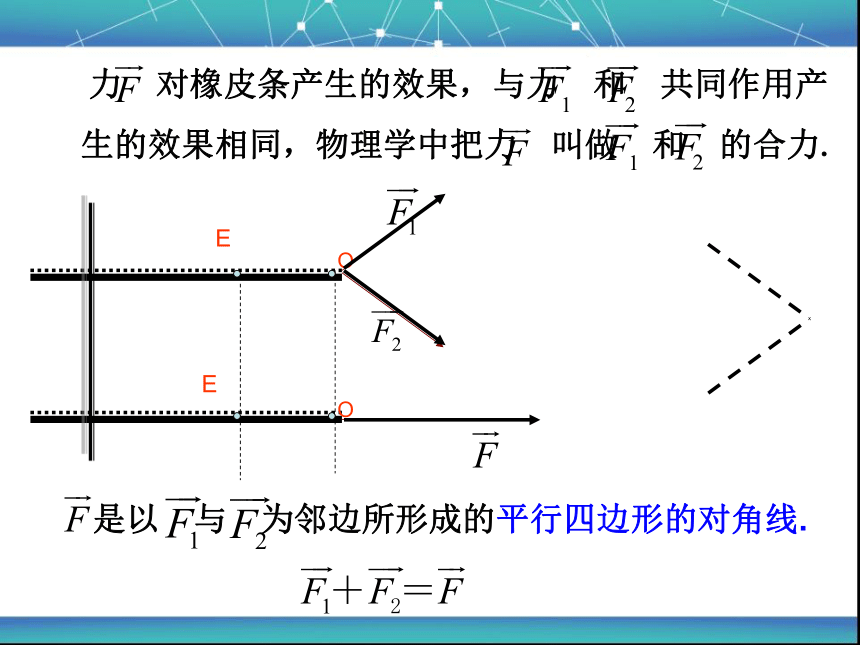
例如:橡皮条在力 与 的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸长到了O点.
问:合力 与力 、 有怎样的关系?
E
O
O
E
是以 与 为邻边所形成的平行四边形的对角线.
力 对橡皮条产生的效果,与力 和 共同作用产生的效果相同,物理学中把力 叫做 和 的合力.
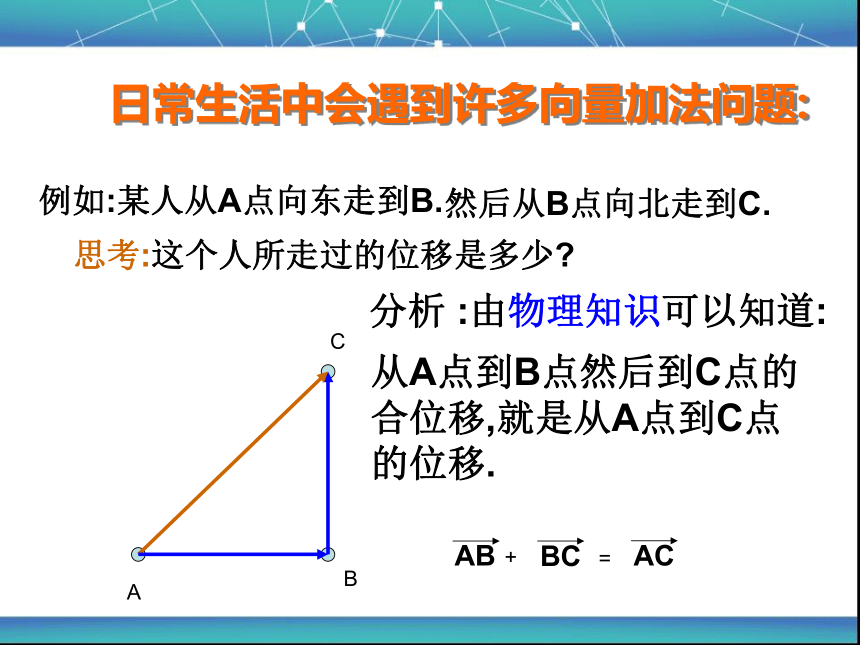
例如:某人从A点向东走到B.
日常生活中会遇到许多向量加法问题:
然后从B点向北走到C.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
向量加法的定义:
我们把求两个向量 的和的运算,叫做向量的加法, 叫做
的和向量.
作法(1)在平面内任取一点O
o·
A
B
位移的合成可以看作向量加法
三角形法则的物理模型.
还有没有其他的做法?
1、向量加法的三角形法则
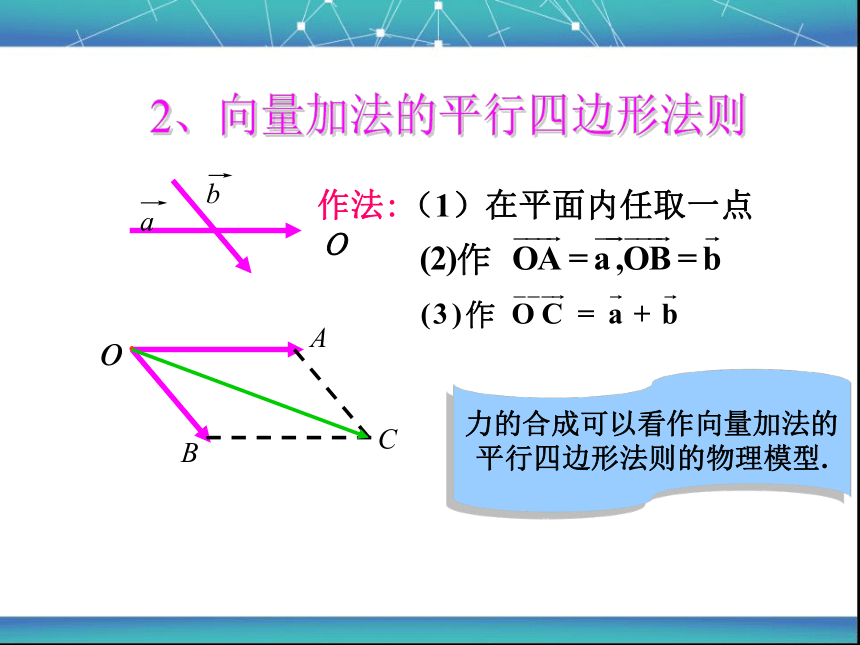
2、向量加法的平行四边形法则
o·
A
B
C
力的合成可以看作向量加法的
平行四边形法则的物理模型.
作法:(1)在平面内任取一点O
向量加法的三角形法则:
1.将向量平移使得它们首尾相连
2.和向量即是第一个向量的首指向第二个向量的尾
向量加法的平行四边形法则:
1.将向量平移到同一起点
2.和向量即以它们作为邻边平行四边形的共起点的对角线
a
b
a
b
a + b
b
a
a + b
问题:除了零向量,有没有不能用平行四边形法则求和向量的情况?
向量加法的三角形法则可推广到多个向量相加,如: 这时也必须“首尾相连”.可结合物理模型“位移的合成”理解.
特例:共线向量
思考???
(1)向同
(2)反向
请选用合适符号连接:
探究
(1)向量加法交换律:
a
b
A
C
D
a + b
a
b
B
向量加法满足交换律和结合律
a
b
c
a
b
c
A
B
C
D
A
B
C
D
a + b
(a + b) + c
a + (b + c)
b + c
(2)向量加法结合律:
以上两个运算律可以推广到任意多个向量.
例2:化简
D
C
B
A
例3:长江两岸之间没有大桥的地方,常常通过轮渡进行运输.一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小和方向.
D
5
C
解:
如图,设 表示水流的速度, 表示渡船的速度,
表示渡船实际过江的速度.(由平行四边形法则可以得到)
若水流速度和船速的大小保持不变,最后要能使渡船垂直过江,则船的航向应该如何?在白纸上作图探究.
D
5
C
探索
1、一个概念: 向量的和;
2、两个法则: 向量加法的三角形法则和平行四
边形法则;
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
课堂小结
数学思想方法方面:
1、具体与抽象的数学思维方法;
2、类比的思想方法.
针对练习
1、若向量a=(1,1),b=(-1,1),c=( )
3a+b B.3a-b
C.-a+3b D.a+3b
B
解析:
本题考查向量的线性运算、逐个验证,3a+b=(2,4),3a-b=(4,2),a+3b=(-2,4)故选B
2、若
则 ( )
A.(1,1) B.(-1,-1)
C.(3,7) D.(-2,-4)
B
解析:
故选B
1.如图:已知向量 , ,求作:
(1)
(4)
(3)
(2)
要求:利用向量加法的三角形法则作出两向量的和.
课堂练习
2.如图:已知向量 , ,求作:
(1)
(2)
要求:利用向量加法的平行四边形法则作出两向量的和.
3.如图:已知平行四边形ABCD,填空
D
C
B
A
+
(1)
=
+
(2)
=
+
+
+
( )
( )
+
(4)
(5)
=
=
+
=
(3)
向南偏西60°走20km.
解:
∵
∴
当 的方向相同时, 取得最大值,最大值为8.
相等向量与相反向量
单位向量与零向量
向 量
向量的大小
(长度、模)
向量的方向
有向线段
平行向量(共线向量)
既有大小又有方向的量叫向量;
向量不能比较大小,但向量的模可以比较大小.
知识回顾
大三通之前,由于大陆和台湾没有直航,因此要从台湾去上海探亲,乘飞机要先从台北到香港,再从香港到上海,这两次位移之和是什么?
新课导入
2.1.2 向量的加法
知识与能力
理解向量的和,掌握向量加法的三角形法则和平行四边形法则,向量加法的运算律.
过程与方法
情感态度与价值观
提高学生观察、归纳、迁移能力和动手能;培养学生的转化思想.
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
教学目标
重点:
难点:
向量加法的三角形法则和平行四边形法则,向量加法的运算律.
对向量和的理解.
教学重难点
E
O
O
E
例如:橡皮条在力 与 的作用下,从E点伸长到了O点.
同时橡皮条在力F的作用下也从E点伸长到了O点.
问:合力 与力 、 有怎样的关系?
E
O
O
E
是以 与 为邻边所形成的平行四边形的对角线.
力 对橡皮条产生的效果,与力 和 共同作用产生的效果相同,物理学中把力 叫做 和 的合力.
例如:某人从A点向东走到B.
日常生活中会遇到许多向量加法问题:
然后从B点向北走到C.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
向量加法的定义:
我们把求两个向量 的和的运算,叫做向量的加法, 叫做
的和向量.
作法(1)在平面内任取一点O
o·
A
B
位移的合成可以看作向量加法
三角形法则的物理模型.
还有没有其他的做法?
1、向量加法的三角形法则
2、向量加法的平行四边形法则
o·
A
B
C
力的合成可以看作向量加法的
平行四边形法则的物理模型.
作法:(1)在平面内任取一点O
向量加法的三角形法则:
1.将向量平移使得它们首尾相连
2.和向量即是第一个向量的首指向第二个向量的尾
向量加法的平行四边形法则:
1.将向量平移到同一起点
2.和向量即以它们作为邻边平行四边形的共起点的对角线
a
b
a
b
a + b
b
a
a + b
问题:除了零向量,有没有不能用平行四边形法则求和向量的情况?
向量加法的三角形法则可推广到多个向量相加,如: 这时也必须“首尾相连”.可结合物理模型“位移的合成”理解.
特例:共线向量
思考???
(1)向同
(2)反向
请选用合适符号连接:
探究
(1)向量加法交换律:
a
b
A
C
D
a + b
a
b
B
向量加法满足交换律和结合律
a
b
c
a
b
c
A
B
C
D
A
B
C
D
a + b
(a + b) + c
a + (b + c)
b + c
(2)向量加法结合律:
以上两个运算律可以推广到任意多个向量.
例2:化简
D
C
B
A
例3:长江两岸之间没有大桥的地方,常常通过轮渡进行运输.一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小和方向.
D
5
C
解:
如图,设 表示水流的速度, 表示渡船的速度,
表示渡船实际过江的速度.(由平行四边形法则可以得到)
若水流速度和船速的大小保持不变,最后要能使渡船垂直过江,则船的航向应该如何?在白纸上作图探究.
D
5
C
探索
1、一个概念: 向量的和;
2、两个法则: 向量加法的三角形法则和平行四
边形法则;
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
课堂小结
数学思想方法方面:
1、具体与抽象的数学思维方法;
2、类比的思想方法.
针对练习
1、若向量a=(1,1),b=(-1,1),c=( )
3a+b B.3a-b
C.-a+3b D.a+3b
B
解析:
本题考查向量的线性运算、逐个验证,3a+b=(2,4),3a-b=(4,2),a+3b=(-2,4)故选B
2、若
则 ( )
A.(1,1) B.(-1,-1)
C.(3,7) D.(-2,-4)
B
解析:
故选B
1.如图:已知向量 , ,求作:
(1)
(4)
(3)
(2)
要求:利用向量加法的三角形法则作出两向量的和.
课堂练习
2.如图:已知向量 , ,求作:
(1)
(2)
要求:利用向量加法的平行四边形法则作出两向量的和.
3.如图:已知平行四边形ABCD,填空
D
C
B
A
+
(1)
=
+
(2)
=
+
+
+
( )
( )
+
(4)
(5)
=
=
+
=
(3)
向南偏西60°走20km.
解:
∵
∴
当 的方向相同时, 取得最大值,最大值为8.
