人教B版高中数学 必修4 第二章 2.1.3向量的减法 同步教学课件(共32张PPT)
文档属性
| 名称 | 人教B版高中数学 必修4 第二章 2.1.3向量的减法 同步教学课件(共32张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 668.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
B
A
C
问题??
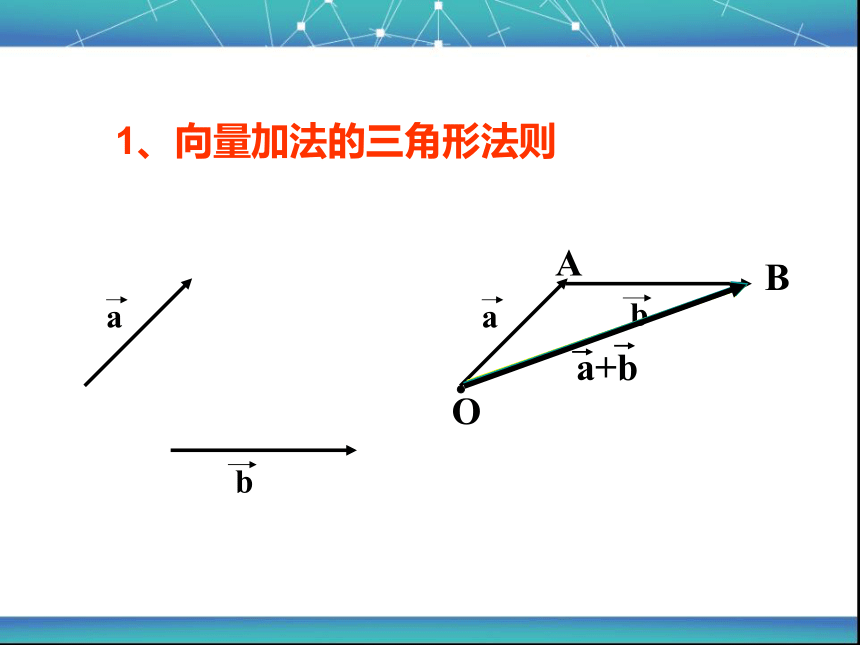
向量 如图,当两个向量相加时,能轻易的在图中表示出来,但是当两个向量想减时,在现有的知识的基础上,能表示出来吗?
它是否是 呢?
新课导入
There is no elevator to success----only stairs.
成功没有电梯,只有一步一个脚印的楼梯.
2.1.3 向量的减法
了解相反向量的概念;会作两个向量的减向量,并理解其几何意义.
教学目标
过程与方法
情感态度与价值观
提高学生观察、归纳、迁移能力和动手能;培养学生的转化思想.
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
知识与能力
重点:
向量的减法运算及其几何意义.
难点:
向量减法的理解.
教学重难点
复习向量加法运算及其几何意义.
温故知新
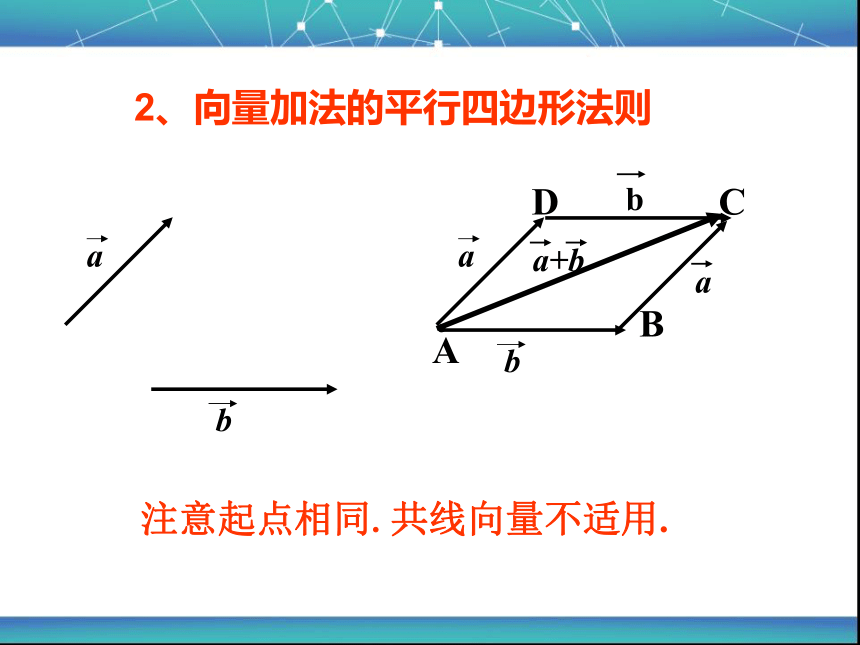
1、向量加法的三角形法则
b
a
O
B
b
a
A
a+b
b
a
A
B
b
a
D
a
C
b
a+b
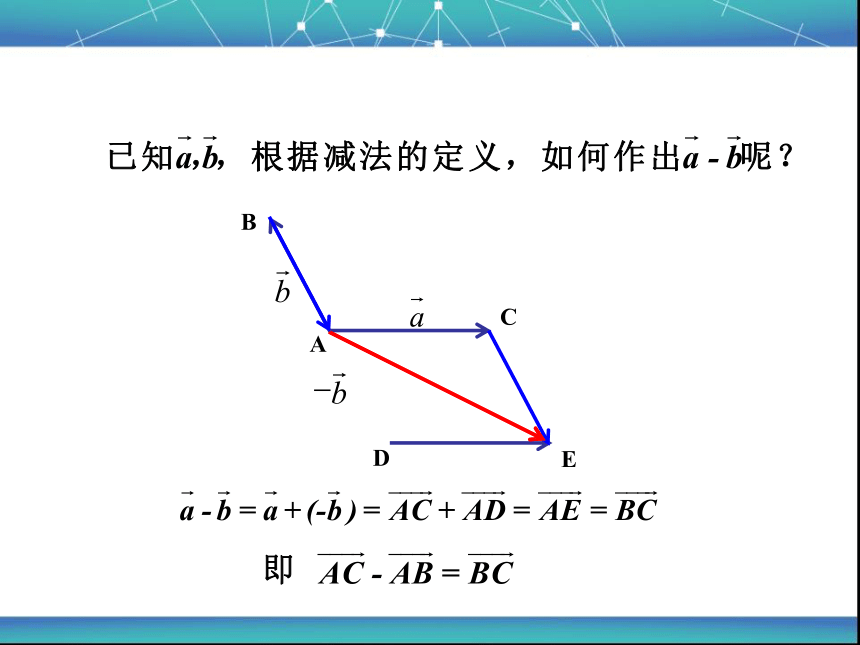
2、向量加法的平行四边形法则
注意起点相同.共线向量不适用.
相反向量定义:
与 长度相同、方向相反的向量.记作
A
C
如图:
规定:零向量的相反向量仍是零向量.
任一向量与它的相反向量的和是零向量.
如果 互为相反向量,则
向量的减法定义:
即减去一个向量相当于加上这个向量的相反向量.
在实数的运算中,减去一个数等于加上这个数的相反数.据此原理,向量 可以怎样理解?
A
B
C
D
E
即
O
B
A
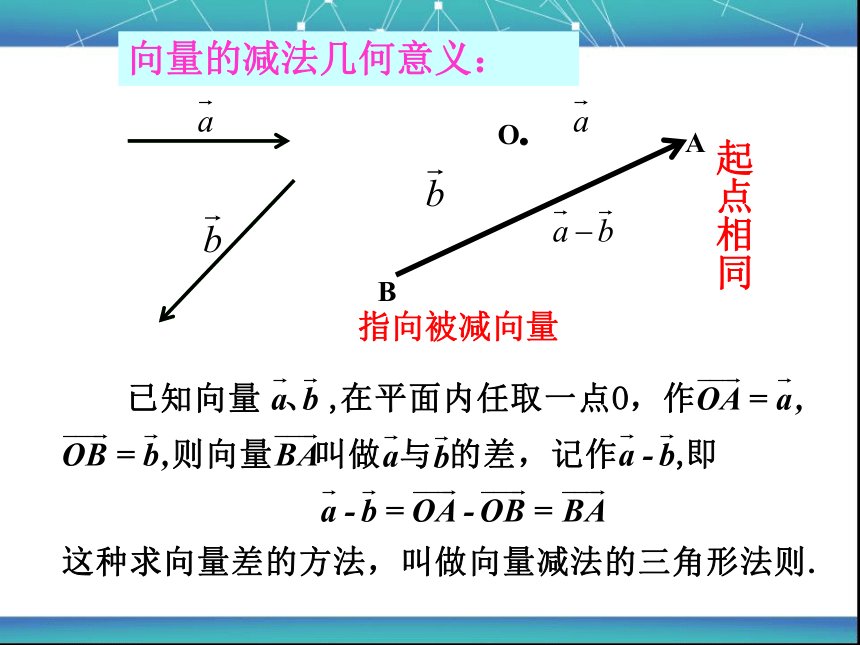
起点相同
指向被减向量
向量的减法几何意义:
?特殊情况
1.共线同向
2.共线反向
B
A
C
A
B
C
a
b
c
d
例1:
如图,已知向量
求作向量 - , - .
a
b
c
d
O
A
B
C
D
作法:
在平面内任取一点O,作
●
例2:选择题
D
C
由向量的减法知
例3:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。
由向量加法的平行四边形法则,我们得到
解:
AC=a+b
DB=a-b
A
D
B
C
证明:
1、理解相反向量的概念
2、 理解向量减法的定义
3、 正确理解掌握根据定义作向量减法,如(3)
4、 正确熟练地掌握向量减法的三角形法则,如(4)
课堂小结
C
D
O
A
B
a
b
.
注意:
1、两个向量相减,则表示两个向量起点的字母必须相同;
2、差向量的终点指向被减向量的终点.
(4)向量减法的三角形法则
针对练习
1、已知平面向量a=(1,1),b=(1,-1),则向量
( )
A.(-2,-1) B.(-2,1)
C.(-1,0) D.(-1,2)
D
解析:
2、若O、E、F是不共面的任意三点,则以下各式中成立的是( )
D.
A.
B.
C.
B
解析:
本题考察了向量的减法法则。由向量的减法知
练习1
课堂练习
练习2
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
作图:
练习3
120o
A
D
B
练习4
120o
A
D
B
C
O`
120o
A
D
B
C
O`
B
A
C
问题??
向量 如图,当两个向量相加时,能轻易的在图中表示出来,但是当两个向量想减时,在现有的知识的基础上,能表示出来吗?
它是否是 呢?
新课导入
There is no elevator to success----only stairs.
成功没有电梯,只有一步一个脚印的楼梯.
2.1.3 向量的减法
了解相反向量的概念;会作两个向量的减向量,并理解其几何意义.
教学目标
过程与方法
情感态度与价值观
提高学生观察、归纳、迁移能力和动手能;培养学生的转化思想.
注重培养学生积极思考、勇于探索的科学精神以及总结规律、尊重规律的观念.
知识与能力
重点:
向量的减法运算及其几何意义.
难点:
向量减法的理解.
教学重难点
复习向量加法运算及其几何意义.
温故知新
1、向量加法的三角形法则
b
a
O
B
b
a
A
a+b
b
a
A
B
b
a
D
a
C
b
a+b
2、向量加法的平行四边形法则
注意起点相同.共线向量不适用.
相反向量定义:
与 长度相同、方向相反的向量.记作
A
C
如图:
规定:零向量的相反向量仍是零向量.
任一向量与它的相反向量的和是零向量.
如果 互为相反向量,则
向量的减法定义:
即减去一个向量相当于加上这个向量的相反向量.
在实数的运算中,减去一个数等于加上这个数的相反数.据此原理,向量 可以怎样理解?
A
B
C
D
E
即
O
B
A
起点相同
指向被减向量
向量的减法几何意义:
?特殊情况
1.共线同向
2.共线反向
B
A
C
A
B
C
a
b
c
d
例1:
如图,已知向量
求作向量 - , - .
a
b
c
d
O
A
B
C
D
作法:
在平面内任取一点O,作
●
例2:选择题
D
C
由向量的减法知
例3:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。
由向量加法的平行四边形法则,我们得到
解:
AC=a+b
DB=a-b
A
D
B
C
证明:
1、理解相反向量的概念
2、 理解向量减法的定义
3、 正确理解掌握根据定义作向量减法,如(3)
4、 正确熟练地掌握向量减法的三角形法则,如(4)
课堂小结
C
D
O
A
B
a
b
.
注意:
1、两个向量相减,则表示两个向量起点的字母必须相同;
2、差向量的终点指向被减向量的终点.
(4)向量减法的三角形法则
针对练习
1、已知平面向量a=(1,1),b=(1,-1),则向量
( )
A.(-2,-1) B.(-2,1)
C.(-1,0) D.(-1,2)
D
解析:
2、若O、E、F是不共面的任意三点,则以下各式中成立的是( )
D.
A.
B.
C.
B
解析:
本题考察了向量的减法法则。由向量的减法知
练习1
课堂练习
练习2
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
作图:
练习3
120o
A
D
B
练习4
120o
A
D
B
C
O`
120o
A
D
B
C
O`
