人教版九年级数学上册 21.2.4 一元二次方程的根与系数关系课件(共22张PPT)
文档属性
| 名称 | 人教版九年级数学上册 21.2.4 一元二次方程的根与系数关系课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 858.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-08 00:00:00 | ||
图片预览







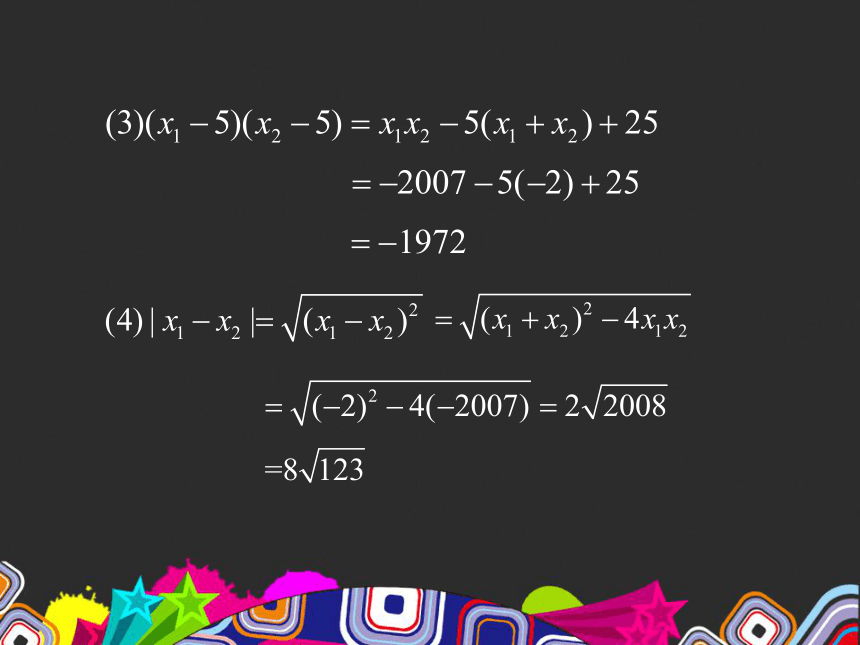

文档简介
(共22张PPT)
一元二次方程的根系关系
【重点导航】
通过学习本课,掌握韦达定理及以下应用:
1.计算对称式的值;
2.构造新方程;
3.研究方程的根的分布情况;
4.求字母系数的取值范围.
一元二次方程的根与系数的关系
【课程精讲】
由此可得,根与系数的关系,也叫韦达定理
练一练
2.已知一元二次方程 的一个
根为1,则:方程的另一根为___,m =___
1.已知一元二次方程 的两根
分别为-2 和 1,则:p = __ ; q =___
韦达定理的应用
1.计算对称式的值
解:由题意,根据根与系数的关系得:
利用韦达定理求值,要熟练掌握以下等式变形:
2.构造新方程
以x1,x2两数为根构造的一元二次方程为:
例2 解方程组
解:显然x,y是方程 z2-5z+6=0 ① 的两根
由方程①解得 z1=2,z2=3
∴原方程组的解为 或
解:由已知,得
∴0例3 方程 有一个 正根,一个负根,求实数m的取值范围。
3.研究方程根的分布情况
解:由题意,根据根与系数的关系得:
解得对么?
正解:由题意,根据根与系数的关系得:
则:
4.求字母系数的取值范围
例5 一个三角形的两边长是方程
的两根,第三边长为2,求k的取值范围。
解:设此三角形的三边长分别为a、b、c,且a、b为
由题意知,△=k2-4×2×2≥0,
解得k≥4或k≤-4
∴ 要使其值是整数,只需k+1能被4整除
【总结提升】
1.首先要把已知一元二次方程化成一般形式. 2.方程有两实根,等价于 .
3.字母的整体代换技巧的应用.
应用韦达定理要注意以下几点:
一元二次方程的根系关系
【重点导航】
通过学习本课,掌握韦达定理及以下应用:
1.计算对称式的值;
2.构造新方程;
3.研究方程的根的分布情况;
4.求字母系数的取值范围.
一元二次方程的根与系数的关系
【课程精讲】
由此可得,根与系数的关系,也叫韦达定理
练一练
2.已知一元二次方程 的一个
根为1,则:方程的另一根为___,m =___
1.已知一元二次方程 的两根
分别为-2 和 1,则:p = __ ; q =___
韦达定理的应用
1.计算对称式的值
解:由题意,根据根与系数的关系得:
利用韦达定理求值,要熟练掌握以下等式变形:
2.构造新方程
以x1,x2两数为根构造的一元二次方程为:
例2 解方程组
解:显然x,y是方程 z2-5z+6=0 ① 的两根
由方程①解得 z1=2,z2=3
∴原方程组的解为 或
解:由已知,得
∴0
3.研究方程根的分布情况
解:由题意,根据根与系数的关系得:
解得对么?
正解:由题意,根据根与系数的关系得:
则:
4.求字母系数的取值范围
例5 一个三角形的两边长是方程
的两根,第三边长为2,求k的取值范围。
解:设此三角形的三边长分别为a、b、c,且a、b为
由题意知,△=k2-4×2×2≥0,
解得k≥4或k≤-4
∴ 要使其值是整数,只需k+1能被4整除
【总结提升】
1.首先要把已知一元二次方程化成一般形式. 2.方程有两实根,等价于 .
3.字母的整体代换技巧的应用.
应用韦达定理要注意以下几点:
同课章节目录
