人教版五年级下册数学试题--2.3《质数和合数》(含答案)
文档属性
| 名称 | 人教版五年级下册数学试题--2.3《质数和合数》(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 551.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 10:11:52 | ||
图片预览


文档简介
质数和合数
第1关 练速度
1.填空题。
(1)质数只有( )个因数,合数至少有( )个因数,( )既不是质数也不是合数。
(2)20以内(含20)的自然数中,质数有( ),合数有( )。
(3)在自然数中,最小的奇数是( ),最小的偶数是( ),最小的质数是( ),最小的合数是( )。
(4)1~9这9个自然数中,相邻的两个合数是( )和( )。
(5)在括号里填上合适的质数。
13=( )+( )
14=( )+( )+( )
24=( )+( )=( )+( )
2.判断题。
(1)所有的质数都是奇数。 ( )
(2)所有的合数都是偶数。 ( )
(3)一个自然数不是质数就是合数。 ( )
(4)两个质数相乘的积一定是合数。 ( )
3.把下面的数填在相应的圆圈里。
2 9 11 23 27 36 51 57 77 81 86 54 97 87
奇数 偶数
质数 合数
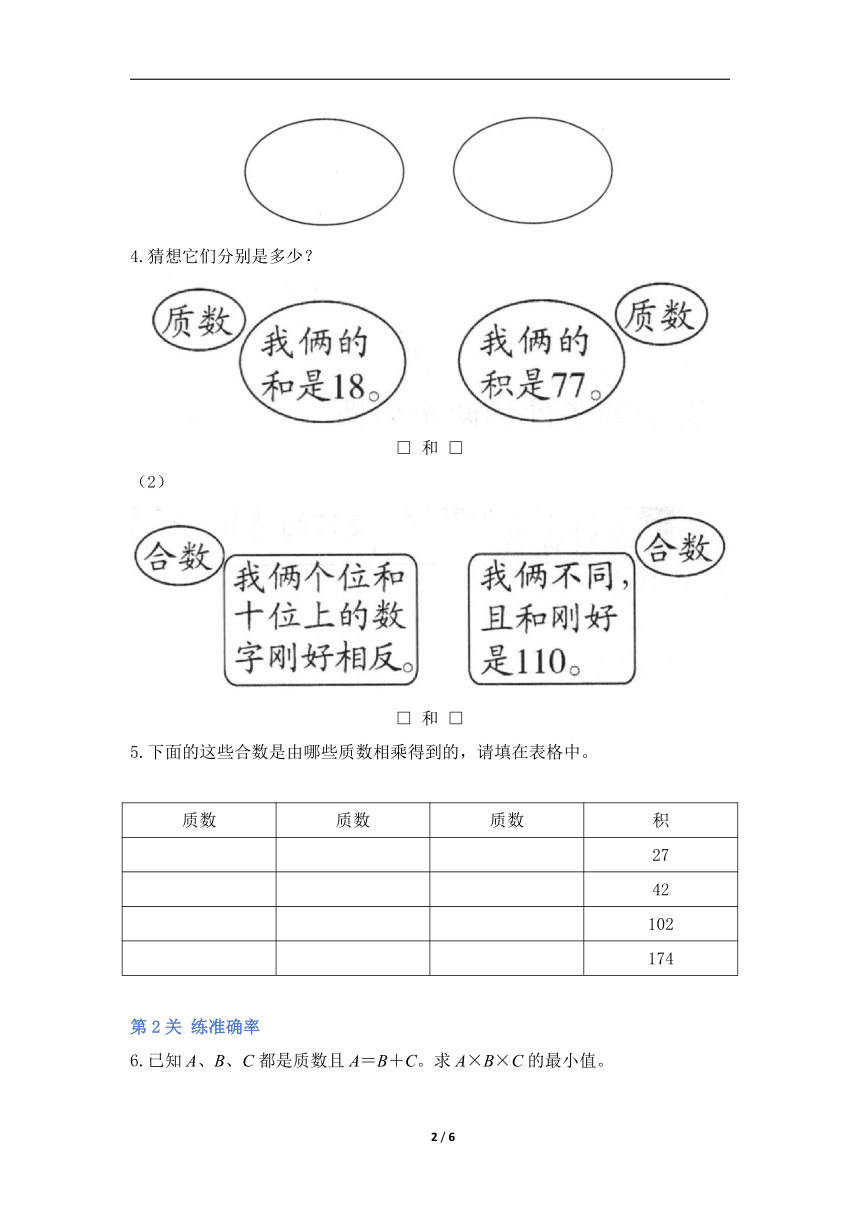
4.猜想它们分别是多少?
□ 和 □
(2)
□ 和 □
5.下面的这些合数是由哪些质数相乘得到的,请填在表格中。
质数
质数
质数
积
27
42
102
174
第2关 练准确率
6.已知A、B、C都是质数且A=B+C。求A×B×C的最小值。
7.有一种两位质数,交换个位与十位上的数字,所得的两位数仍是质数。这种数我们称为“幸运数”,那么这样的“幸运数”有哪些?
8.求符合下列条件的两个质数。
9.5个连续的自然数,每个数都是合数,这5个自然数的和最小是多少?
10.a、b、c都是质数,并且a+b=33,b+c=44,c+d=66。求d的值。
11.如果a、b均为质数,且3a+7b=41。求a+b。
第3关 练思维
12.两个质数的和是40,这两个质数的乘积最大是多少?
13.用1、3、5、7、9这五个数字组成若干个合数,每个数字恰好用一次,那么,这些合数的总和最小是多少?
14.大约1500多年前我国伟大的数学家祖冲之计算出π的值在3.1415926和3.1415927之间,成为世界上第一个把丌的值精确到七位小数的人。现代人利用计算机已经将丌的值计算到了小数点后15亿位以上。这些数排列既无序又无规律。但是细心的同学发现:由左起的第一位3是质数,31也是质数,但314不是质数,那么在3141、31415、314159、3141592、31415926、31415927中,哪些是质数?
参考答案
1.(1)2 3 1
(2)2、3、57、11、13、17、19 4、6、8、9、10、12、14、15、16、18、20
(3)1 0 2 4
(4)8 9
(5)2 11 2 5 7 17 7 11 13(或19 5)
2.(1)× (2)× (3)× (4)√
3.奇数:9、11、23、27、51、57、77、81、97、87
偶数:2、36、86、54
质数:2、11、23、97
合数:9、27、36、51、57、77、81、86、54、87
4.(1)7 11 (2)28 82(或46 64)
5.3 3 3 2 3 7 2 3 17 2 3 29
6.30 提示:要使A×B×C最小,则A、B、C尽可能是较小的质数,而5=2+3,所以A=5,B=2,C=3,A×B×C=5×3×2=30。
7.这样的“幸运数”有:11、13、17、31、37、71、73、79、97。 提示:把两位质数写下来,再看看哪些质数交换十位与个位后仍是质数,符合条件的两位质数有:11、13、17、31、37、71、73、7997。
8.两个质数分别为83和2。 提示:小于100的17的奇数倍数有:17、51、85,而15+2=17,49+2=51,83+2=85,只有83和2符合条件。
9.130 提示:要使这5个自然数的和最小,则这5个数均应为连续较小自然数,又都是合数。在自然数中从较小数开始连续5个合数有24,25,26,27,28,所以这5个自然数的和为24+25+26+27+28=130。
10.53 提示:a、b、c均为质数,而a+b=33,则a,b中有个数为2,另一个数是31,因为b+c=44,则b=31,c=13。又因为c+d=66,则d=66-13=53
11.a+b=7 提示:若a、b既是质数,又是奇数,则3a+7b≠41(奇数),故a、b中有一个数为2。当a=2时,3×2+7b=41,b=5,符合题意;当b=2时,3a+72=41,a=9,不符合题意。所以a+b=2+5=7。
12.391 提示:小于40的质数有2,3,5,7,11,13,17,19,23,29,31,37,其中两个质数的和是40的有3和37,11和29,17和23,它们的积分别是3×37=11,
11×29=319,17×23=391,比较发现最大是391。
13.214 提示:若组成的合数中最大的为两位数,而1、3、5、7、9中合数只有9,则为2个两位合数和1个位合数,但13、31、37、73、17、71是质数,所以此时无解。若组成的合数中最大的为三位数,而1、3、5、7、9中合数只有9,则为1个三位合数和1个两位合数,又137、139、157都是质数,所以百位上至少是1,十位上的数字之和至少是3+7=10,于是这些合数的总和至少是1×100+10×10+5+9=214,而175+39=214,所以这些合数的总和最小是214。
14.314159 提示:把容易看出的合数先排除掉,3141、31415、3141592、31415926分别是3、5、2、2的倍数,所以均为合数。而31415927又是31的倍数,所以只有314159为质数。
第1关 练速度
1.填空题。
(1)质数只有( )个因数,合数至少有( )个因数,( )既不是质数也不是合数。
(2)20以内(含20)的自然数中,质数有( ),合数有( )。
(3)在自然数中,最小的奇数是( ),最小的偶数是( ),最小的质数是( ),最小的合数是( )。
(4)1~9这9个自然数中,相邻的两个合数是( )和( )。
(5)在括号里填上合适的质数。
13=( )+( )
14=( )+( )+( )
24=( )+( )=( )+( )
2.判断题。
(1)所有的质数都是奇数。 ( )
(2)所有的合数都是偶数。 ( )
(3)一个自然数不是质数就是合数。 ( )
(4)两个质数相乘的积一定是合数。 ( )
3.把下面的数填在相应的圆圈里。
2 9 11 23 27 36 51 57 77 81 86 54 97 87
奇数 偶数
质数 合数
4.猜想它们分别是多少?
□ 和 □
(2)
□ 和 □
5.下面的这些合数是由哪些质数相乘得到的,请填在表格中。
质数
质数
质数
积
27
42
102
174
第2关 练准确率
6.已知A、B、C都是质数且A=B+C。求A×B×C的最小值。
7.有一种两位质数,交换个位与十位上的数字,所得的两位数仍是质数。这种数我们称为“幸运数”,那么这样的“幸运数”有哪些?
8.求符合下列条件的两个质数。
9.5个连续的自然数,每个数都是合数,这5个自然数的和最小是多少?
10.a、b、c都是质数,并且a+b=33,b+c=44,c+d=66。求d的值。
11.如果a、b均为质数,且3a+7b=41。求a+b。
第3关 练思维
12.两个质数的和是40,这两个质数的乘积最大是多少?
13.用1、3、5、7、9这五个数字组成若干个合数,每个数字恰好用一次,那么,这些合数的总和最小是多少?
14.大约1500多年前我国伟大的数学家祖冲之计算出π的值在3.1415926和3.1415927之间,成为世界上第一个把丌的值精确到七位小数的人。现代人利用计算机已经将丌的值计算到了小数点后15亿位以上。这些数排列既无序又无规律。但是细心的同学发现:由左起的第一位3是质数,31也是质数,但314不是质数,那么在3141、31415、314159、3141592、31415926、31415927中,哪些是质数?
参考答案
1.(1)2 3 1
(2)2、3、57、11、13、17、19 4、6、8、9、10、12、14、15、16、18、20
(3)1 0 2 4
(4)8 9
(5)2 11 2 5 7 17 7 11 13(或19 5)
2.(1)× (2)× (3)× (4)√
3.奇数:9、11、23、27、51、57、77、81、97、87
偶数:2、36、86、54
质数:2、11、23、97
合数:9、27、36、51、57、77、81、86、54、87
4.(1)7 11 (2)28 82(或46 64)
5.3 3 3 2 3 7 2 3 17 2 3 29
6.30 提示:要使A×B×C最小,则A、B、C尽可能是较小的质数,而5=2+3,所以A=5,B=2,C=3,A×B×C=5×3×2=30。
7.这样的“幸运数”有:11、13、17、31、37、71、73、79、97。 提示:把两位质数写下来,再看看哪些质数交换十位与个位后仍是质数,符合条件的两位质数有:11、13、17、31、37、71、73、7997。
8.两个质数分别为83和2。 提示:小于100的17的奇数倍数有:17、51、85,而15+2=17,49+2=51,83+2=85,只有83和2符合条件。
9.130 提示:要使这5个自然数的和最小,则这5个数均应为连续较小自然数,又都是合数。在自然数中从较小数开始连续5个合数有24,25,26,27,28,所以这5个自然数的和为24+25+26+27+28=130。
10.53 提示:a、b、c均为质数,而a+b=33,则a,b中有个数为2,另一个数是31,因为b+c=44,则b=31,c=13。又因为c+d=66,则d=66-13=53
11.a+b=7 提示:若a、b既是质数,又是奇数,则3a+7b≠41(奇数),故a、b中有一个数为2。当a=2时,3×2+7b=41,b=5,符合题意;当b=2时,3a+72=41,a=9,不符合题意。所以a+b=2+5=7。
12.391 提示:小于40的质数有2,3,5,7,11,13,17,19,23,29,31,37,其中两个质数的和是40的有3和37,11和29,17和23,它们的积分别是3×37=11,
11×29=319,17×23=391,比较发现最大是391。
13.214 提示:若组成的合数中最大的为两位数,而1、3、5、7、9中合数只有9,则为2个两位合数和1个位合数,但13、31、37、73、17、71是质数,所以此时无解。若组成的合数中最大的为三位数,而1、3、5、7、9中合数只有9,则为1个三位合数和1个两位合数,又137、139、157都是质数,所以百位上至少是1,十位上的数字之和至少是3+7=10,于是这些合数的总和至少是1×100+10×10+5+9=214,而175+39=214,所以这些合数的总和最小是214。
14.314159 提示:把容易看出的合数先排除掉,3141、31415、3141592、31415926分别是3、5、2、2的倍数,所以均为合数。而31415927又是31的倍数,所以只有314159为质数。
