第5章 走进图形世界单元测试卷（含解析）

中小学教育资源及组卷应用平台
第五章测试卷
一、选择题（每题3分，共30分）
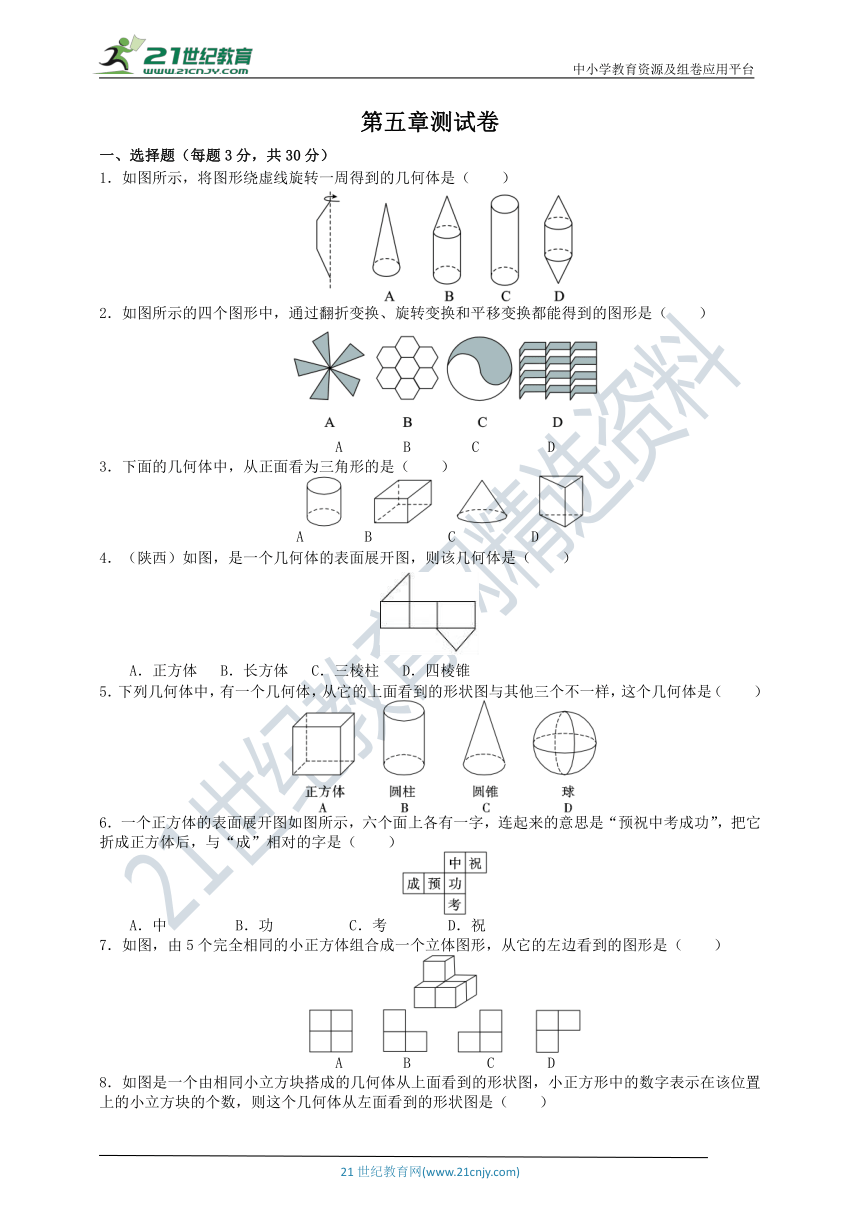
1．如图所示，将图形绕虚线旋转一周得到的几何体是（　　）
2．如图所示的四个图形中，通过翻折变换、旋转变换和平移变换都能得到的图形是（　　）
A　　
　
B　　
　
C　　
　　D
3．下面的几何体中，从正面看为三角形的是（
）
A
　　　B　
　
　C　
　
　D
4．（陕西）如图，是一个几何体的表面展开图，则该几何体是（
）
A．正方体
B．长方体
C．三棱柱
D．四棱锥
5．下列几何体中，有一个几何体，从它的上面看到的形状图与其他三个不一样，这个几何体是（
）
6．一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“预祝中考成功”，把它折成正方体后，与“成”相对的字是（
）
A．中
B．功
C．考
D．祝
7．如图，由5个完全相同的小正方体组合成一个立体图形，从它的左边看到的图形是（
）
A　　　　B　　　　　C　　　
D
8．如图是一个由相同小立方块搭成的几何体从上面看到的形状图，小正方形中的数字表示在该位置上的小立方块的个数，则这个几何体从左面看到的形状图是（
）
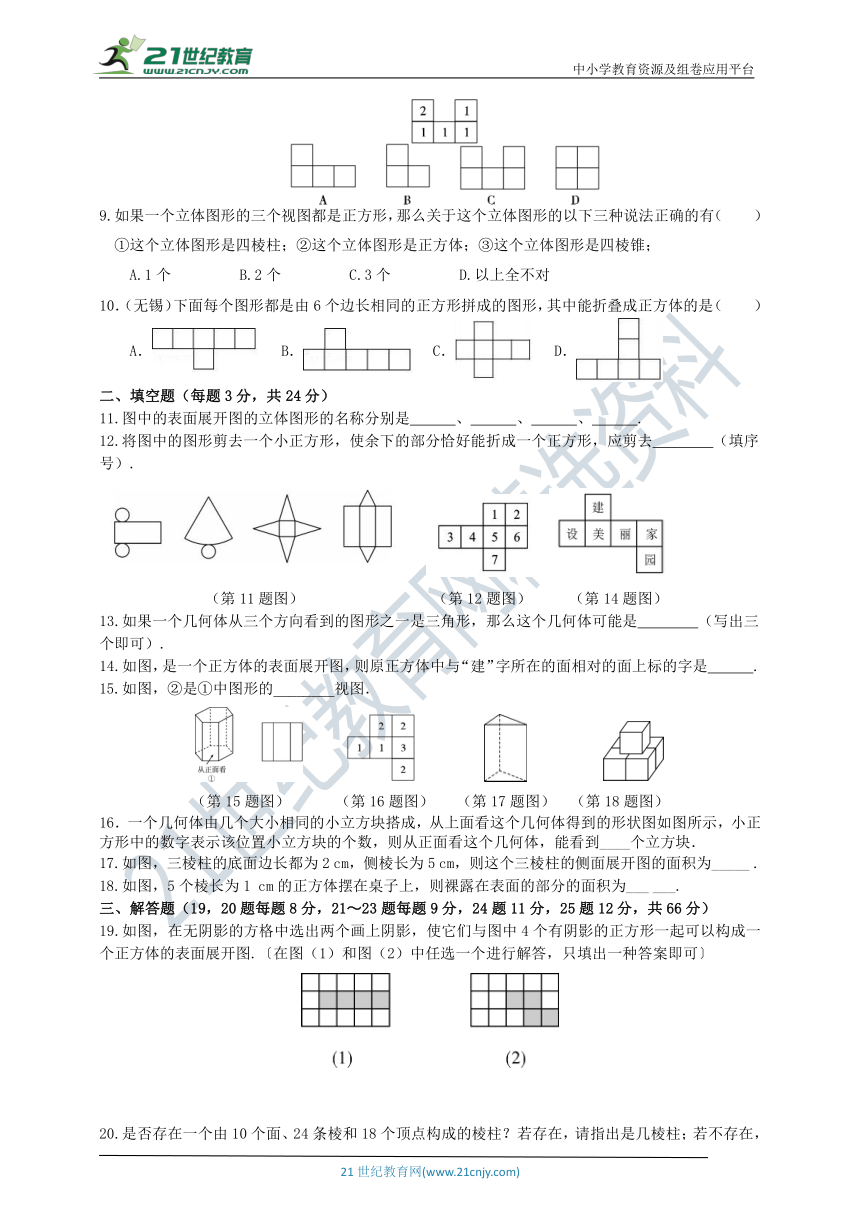
9.如果一个立体图形的三个视图都是正方形，那么关于这个立体图形的以下三种说法正确的有（
）
①这个立体图形是四棱柱；②这个立体图形是正方体；③这个立体图形是四棱锥；
A.1个
B.2个
C.3个
D.以上全不对
10．（无锡）下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（
）
A．
B．
C．
D．
二、填空题（每题3分，共24分）
11.图中的表面展开图的立体图形的名称分别是
、
、
、
.
12.将图中的图形剪去一个小正方形，使余下的部分恰好能折成一个正方形，应剪去
（填序号）.
（第11题图）
（第12题图）
（第14题图）
13.如果一个几何体从三个方向看到的图形之一是三角形，那么这个几何体可能是
（写出三个即可）.
14.如图，是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的字是
.
15.如图，②是①中图形的________视图．
（第15题图）
（第16题图）
（第17题图）
（第18题图）
16．一个几何体由几个大小相同的小立方块搭成，从上面看这个几何体得到的形状图如图所示，小正方形中的数字表示该位置小立方块的个数，则从正面看这个几何体，能看到____个立方块．
17.如图，三棱柱的底面边长都为2
cm，侧棱长为5
cm，则这个三棱柱的侧面展开图的面积为_____
.
18.如图，5个棱长为1
cm的正方体摆在桌子上，则裸露在表面的部分的面积为___
___.
三、解答题（19，20题每题8分，21～23题每题9分，24题11分，25题12分，共66分）
19.如图，在无阴影的方格中选出两个画上阴影，使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.〔在图（1）和图（2）中任选一个进行解答，只填出一种答案即可〕
20.是否存在一个由10个面、24条棱和18个顶点构成的棱柱？若存在，请指出是几棱柱；若不存在，请说明理由.
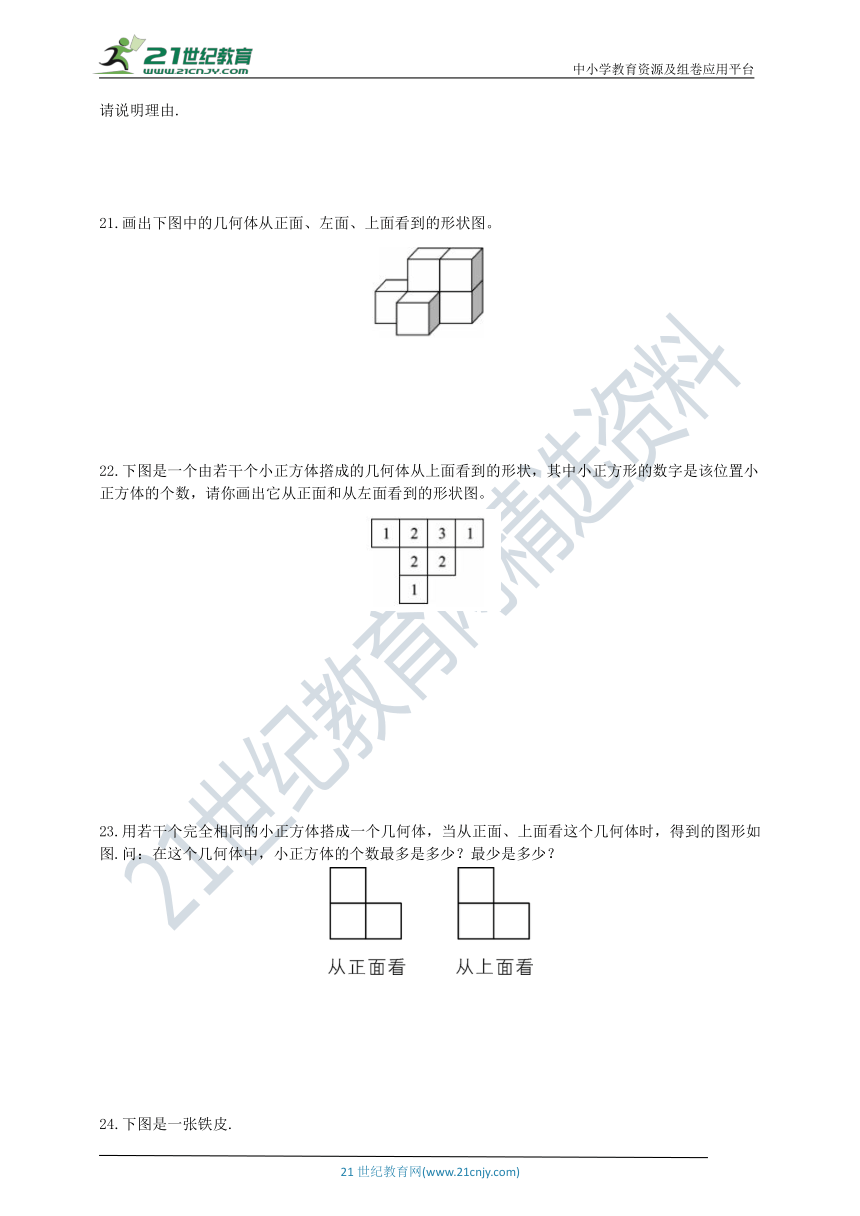
21.画出下图中的几何体从正面、左面、上面看到的形状图。
22.下图是一个由若干个小正方体撘成的几何体从上面看到的形状，其中小正方形的数字是该位置小正方体的个数，请你画出它从正面和从左面看到的形状图。
23.用若干个完全相同的小正方体搭成一个几何体，当从正面、上面看这个几何体时，得到的图形如图.问：在这个几何体中，小正方体的个数最多是多少？最少是多少？
24.下图是一张铁皮.
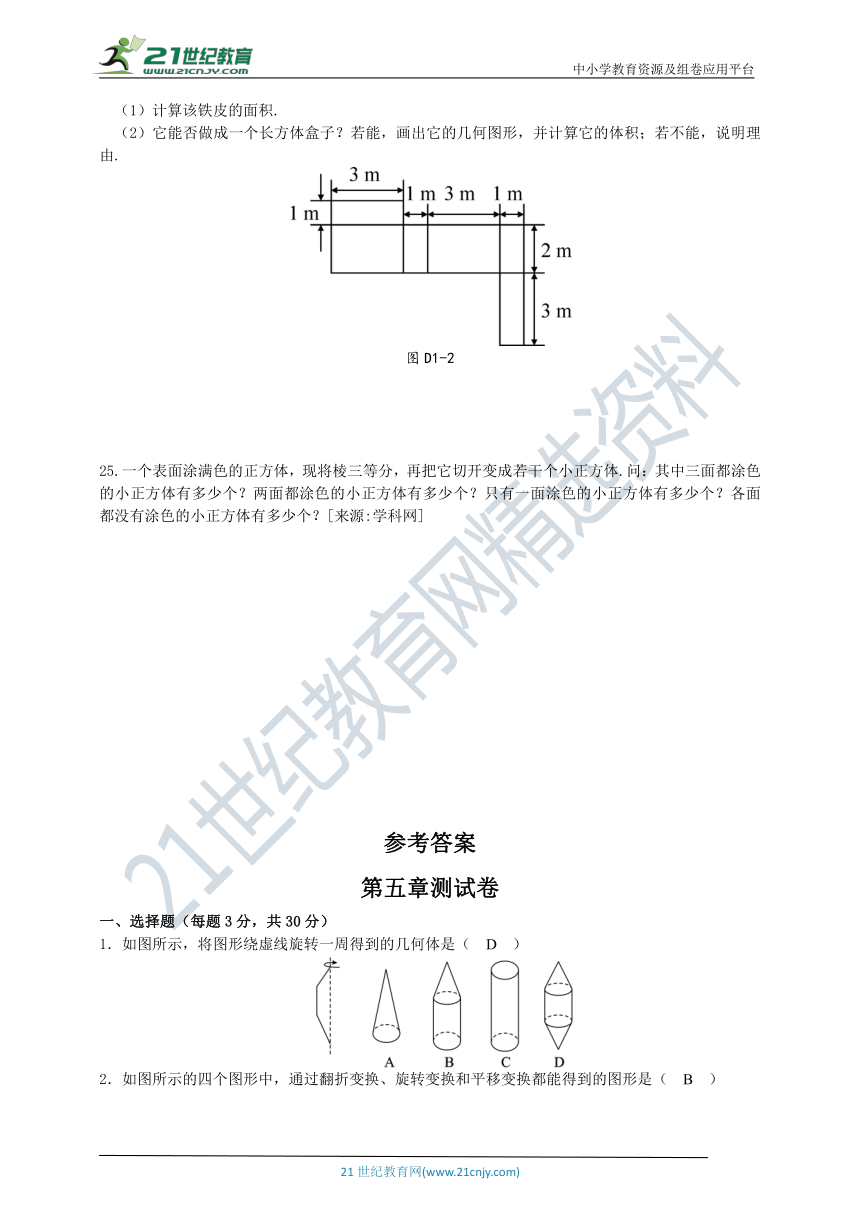
（1）计算该铁皮的面积.
（2）它能否做成一个长方体盒子？若能，画出它的几何图形，并计算它的体积；若不能，说明理由.
图D1-2
25.一个表面涂满色的正方体，现将棱三等分，再把它切开变成若干个小正方体.问：其中三面都涂色的小正方体有多少个？两面都涂色的小正方体有多少个？只有一面涂色的小正方体有多少个？各面都没有涂色的小正方体有多少个？[]
参考答案
第五章测试卷
一、选择题（每题3分，共30分）
1．如图所示，将图形绕虚线旋转一周得到的几何体是（　D　）
2．如图所示的四个图形中，通过翻折变换、旋转变换和平移变换都能得到的图形是（　B　）
A　　
　
B　　
　
C　　
　　D
3．下面的几何体中，从正面看为三角形的是（
C
）
A
　　　B　
　
　C　
　
　D
4．（陕西）如图，是一个几何体的表面展开图，则该几何体是（
C
）
A．正方体
B．长方体
C．三棱柱
D．四棱锥
5．下列几何体中，有一个几何体，从它的上面看到的形状图与其他三个不一样，这个几何体是（
A
）
6．一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“预祝中考成功”，把它折成正方体后，与“成”相对的字是（
B
）
A．中
B．功
C．考
D．祝
7．如图，由5个完全相同的小正方体组合成一个立体图形，从它的左边看到的图形是（
B
）
A　　　　B　　　　　C　　　
D
8．如图是一个由相同小立方块搭成的几何体从上面看到的形状图，小正方形中的数字表示在该位置上的小立方块的个数，则这个几何体从左面看到的形状图是（
B
）
9.如果一个立体图形的三个视图都是正方形，那么关于这个立体图形的以下三种说法正确的有（
B
）
①这个立体图形是四棱柱；②这个立体图形是正方体；③这个立体图形是四棱锥；
A.1个
B.2个
C.3个
D.以上全不对
【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．解答：正方体也是四棱柱；正方体的三视图均为正方形；四棱锥是三视图为三角形，三角形，四边形和两条对角线；符合的有①②．故选B．
10．（无锡）下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（
C
）
A．
B．
C．
D．
【解析】利用正方体及其表面展开图的特点解题．能组成正方体的“一，四，一”“三，三”“二，二，二”“一，三，二”的基本形态要记牢．故能折叠成正方体的是C．
二、填空题（每题3分，共24分）
11.图中的表面展开图的立体图形的名称分别是
圆柱
、
圆锥
、
四棱锥
、
三棱柱
.
12.将图中的图形剪去一个小正方形，使余下的部分恰好能折成一个正方形，应剪去
1或2或6
（填序号）.
（第11题图）
（第12题图）
（第14题图）
13.如果一个几何体从三个方向看到的图形之一是三角形，那么这个几何体可能是
圆锥、三棱柱、三棱锥等（答案不唯一）
（写出三个即可）.
14.如图，是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的字是
园
.
15.如图，②是①中图形的____主____视图．
（第15题图）
（第16题图）
（第17题图）
（第18题图）
16．一个几何体由几个大小相同的小立方块搭成，从上面看这个几何体得到的形状图如图所示，小正方形中的数字表示该位置小立方块的个数，则从正面看这个几何体，能看到__6__个立方块．
17.如图，三棱柱的底面边长都为2
cm，侧棱长为5
cm，则这个三棱柱的侧面展开图的面积为___30
cm2__
.
【解析】三棱柱的侧面展开图是一个长方形，且长方形的长为三棱柱的底面周长，长方形的宽为三棱柱的高,则其侧面展开图的面积为2×3×5=30（cm2）.
18.如图，5个棱长为1
cm的正方体摆在桌子上，则裸露在表面的部分的面积为___16
cm2
___.
【解析】摆放在桌面上的5个正方体的裸露部分，我们可以从前、后、左、右
和上面5个角度去观察，而前、后、左、右4个角度各能观察到3个正方形，加之从上面观察实际可以看到4个正方形的面积，因此几何体的裸露部分的面积是16
cm2
.
三、解答题（19，20题每题8分，21～23题每题9分，24题11分，25题12分，共66分）
19.如图，在无阴影的方格中选出两个画上阴影，使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.〔在图（1）和图（2）中任选一个进行解答，只填出一种答案即可〕
解：如图D1-1，从图（1）（2）的所有图中只要画出一种即可.
（2）
20.是否存在一个由10个面、24条棱和18个顶点构成的棱柱？若存在，请指出是几棱柱；若不存在，请说明理由.
解：不存在.理由：因为有10个面的棱柱一定是八棱柱，而八棱柱有24条棱，但它不是18个顶点,而是16个顶点.
21.画出下图中的几何体从正面、左面、上面看到的形状图。
解：如图：
22.下图是一个由若干个小正方体撘成的几何体从上面看到的形状，其中小正方形的数字是该位置小正方体的个数，请你画出它从正面和从左面看到的形状图。
解：从正面和从左面看到的形状图如图：
23.用若干个完全相同的小正方体搭成一个几何体，当从正面、上面看这个几何体时，得到的图形如图.问：在这个几何体中，小正方体的个数最多是多少？最少是多少？
解：根据已知可得，在从上面看到的图形中，各位置上小正方体的个数最多时如图D1-3（1），各位置上小正方体的个数最少时如图.
由图（1）可知，这个几何体中有5个小正方体；由图（2）可知，这个几何体中有4个小正方体.即在这个几何体中，小正方体的个数最多是5，最少是4.
24.下图是一张铁皮.
（1）计算该铁皮的面积.
（2）它能否做成一个长方体盒子？若能，画出它的几何图形，并计算它的体积；若不能，说明理由.
图D1-2
解：（1）该铁皮的面积为（1×3）×2+（2×3）×2+（1×2）×2=22（m2）.
（2）能做成一个长方体盒子，如图.
其体积为3×1×2=6（m3）.
25.一个表面涂满色的正方体，现将棱三等分，再把它切开变成若干个小正方体.问：其中三面都涂色的小正方体有多少个？两面都涂色的小正方体有多少个？只有一面涂色的小正方体有多少个？各面都没有涂色的小正方体有多少个？[]
解：由题意知,各顶点处的小正方体的三面都涂色，共有8个；有一条边在棱上的小正方体有12个，是两面涂色；每个面的正中间有一个只有一面涂色的，有6个；正方体正中心处有1个小正方体，它的各面都没有涂色．因此三面涂色的小正方体有8个，两面涂色的小正方体有12个，只有一面涂色的小正方体有6个，各面都没有涂色的小正方体有1个．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
21世纪教育网(www.21cnjy.com)