1.2 矩形的性质与判定(2)同步练习题(含答案)
文档属性
| 名称 | 1.2 矩形的性质与判定(2)同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 12:11:38 | ||
图片预览


文档简介
第一章 特殊平行四边形
4 矩形的性质与判定(2)
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( )
A.AO=CO,BO=DO B.AO=BO=CO=DO
C.AC=BD,AO=CO D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
4.如图,在□ABCD中,对角线AC,BD相交于点O,OA=2,若要使□ABCD为矩形,则OB的长应该为( )
A.4 B.3 C.2 D.1
(第4题图) (第5题图 ) (第6题图)
5.如图,要使平行四边形ABCD是矩形,则应添加的条件是_ ___.(添加一个条件即可)
6.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为____度时,四边形ABFE为矩形.
7.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为____.
8.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件 _ _时,四边形PEMF为矩形.
9.已知□ABCD的对角线交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使□ABCD是矩形的条件的序号是 .
10.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
11.已知,如图,在□ABCD中,对角线AC,BD相交于点O,且△OAB是等边三角形,若□ABCD的面积是16,求对角线AC的长.
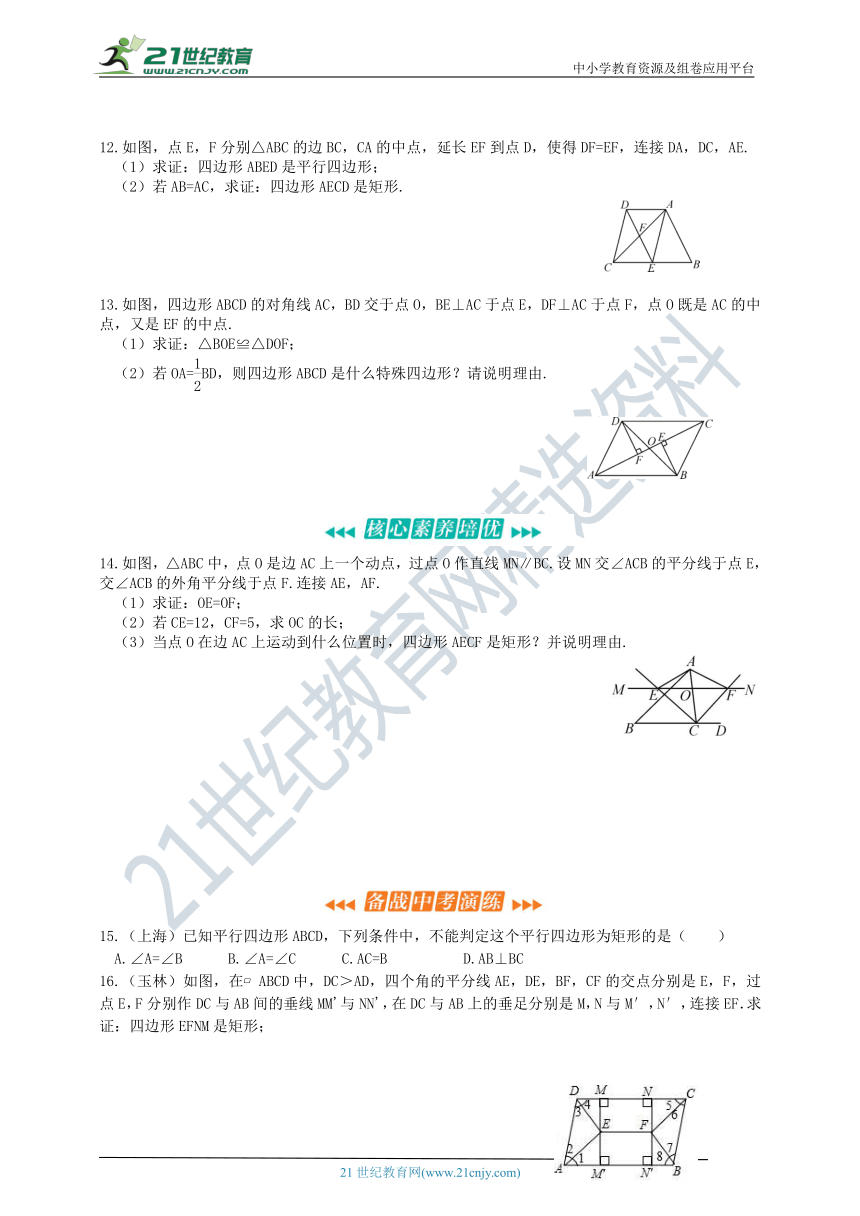
12.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
13.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
14.如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
15.(上海)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=B D.AB⊥BC
16.(玉林)如图,在?ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.求证:四边形EFNM是矩形;
参考答案
第一章 特殊平行四边形
4 矩形的性质与判定(2)
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( B )
A.AO=CO,BO=DO B.AO=BO=CO=DO
C.AC=BD,AO=CO D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( C )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
4.如图,在□ABCD中,对角线AC,BD相交于点O,OA=2,若要使□ABCD为矩形,则OB的长应该为( C )
A.4 B.3 C.2 D.1
(第4题图) (第5题图 ) (第6题图)
5.如图,要使平行四边形ABCD是矩形,则应添加的条件是__∠ABC=90°或AC=BD(答案不唯一)__.(添加一个条件即可)
6.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__60__度时,四边形ABFE为矩形.
7.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为__12__.
8.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件BC=2AB _时,四边形PEMF为矩形.
9.已知□ABCD的对角线交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使□ABCD是矩形的条件的序号是__①③④__.
10.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
解:证明:∵AC=AB,AD=AE,∠BAD=∠CAE,∴∠CAD=∠BAD-∠CAB=∠CAE-∠CAB=∠BAE.∴△ADC≌△AEB.∴DC=BE,∠ABE=∠ACD.又∵DE=BC,∴四边形BCDE为平行四边形.∵AB=AC,∴∠ABC=ACB,∴∠ABC+∠ABE=∠ACB+∠ACD,即∠EBC=∠DCB=90°.∴四边形BCED为矩形
11.已知,如图,在□ABCD中,对角线AC,BD相交于点O,且△OAB是等边三角形,若□ABCD的面积是16,求对角线AC的长.
解:∵△OAB是等边三角形,∴OA=OB,∠OAB=60°,又∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴AC=BD,∴?ABCD是矩形,∴∠ABC=90°,∵∠OAB=60°,∴∠ACB=30°,∴AC=2AB,BC=AB,∴AB·AB=16,∴AB=4,∴AC=8
12.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
解:(1)证明:∵AF=CF,DF=EF,∴四边形AECD是平行四边形,∴AD∥BC,AD=CE,又∵BE=CE,∴AD=BE,∴四边形ABED是平行四边形.
(2)∵AB=AC,BE=CE,∴AE⊥BC,∴∠AEC=90°,∴□ABCD是矩形.
13.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
解:(1)证明:∵BE⊥AC,DF⊥AC,∴∠BEO=∠DFO=90°,∵点O是EF的中点,∴OE=OF,又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).
(2)四边形ABCD是矩形.理由如下:∵△BOE≌△DOF,∴OB=OD,又∵OA=OC,∴四边形ABCD是平行四边形,∵OA=BD,OA=AC,∴BD=AC,∴□ABCD是矩形.
14.如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:∵CF平分∠ACD,且MN∥BD,∴∠ACF=∠FCD=∠CFO.∴OF=OC.同理可证:OC=OE.∴OE=OF.
由(1)知:OF=OC,OC=OE,∴∠OCF=∠OFC,∠OCE=∠OEC.∴∠OCF+∠OCE=∠OFC+∠OEC.而∠OCF+∠OCE+∠OFC+∠OEC=180°,∴∠ECF=∠OCF+∠OCE=90°,∴EF===13.∴OC=EF=.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形..理由如下:由(1)知OE=OF, 当点O移动到AC中点时有OA=OC,∴四边形AECF是平行四边形, ∵∠ECF=90°, ∴平行四边形AECF是矩形.
15.(上海)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( B )
A.∠A=∠B B.∠A=∠C C.AC=B D.AB⊥BC
16.(玉林)如图,在?ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.求证:四边形EFNM是矩形;
证明:过点E、F分别作AD、BC的垂线,垂足分别是G、H.∵∠3=∠4,∠1=∠2,EG⊥AD,EM⊥CD,EM′⊥AB∴EG=ME,EG=EM′
∴EG=ME=ME′=MM′,
同理可证:FH=NF=N′F=NN′,
∵CD∥AB,MM′⊥CD,NN′⊥CD,
∴MM′=NN′,∴ME=NF=EG=FH,
又∵MM′∥NN′,MM′⊥CD,
∴四边形EFNM是矩形.
4 矩形的性质与判定(2)
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( )
A.AO=CO,BO=DO B.AO=BO=CO=DO
C.AC=BD,AO=CO D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
4.如图,在□ABCD中,对角线AC,BD相交于点O,OA=2,若要使□ABCD为矩形,则OB的长应该为( )
A.4 B.3 C.2 D.1
(第4题图) (第5题图 ) (第6题图)
5.如图,要使平行四边形ABCD是矩形,则应添加的条件是_ ___.(添加一个条件即可)
6.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为____度时,四边形ABFE为矩形.
7.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为____.
8.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件 _ _时,四边形PEMF为矩形.
9.已知□ABCD的对角线交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使□ABCD是矩形的条件的序号是 .
10.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
11.已知,如图,在□ABCD中,对角线AC,BD相交于点O,且△OAB是等边三角形,若□ABCD的面积是16,求对角线AC的长.
12.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
13.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
14.如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
15.(上海)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=B D.AB⊥BC
16.(玉林)如图,在?ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.求证:四边形EFNM是矩形;
参考答案
第一章 特殊平行四边形
4 矩形的性质与判定(2)
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( B )
A.AO=CO,BO=DO B.AO=BO=CO=DO
C.AC=BD,AO=CO D.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( D )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直平分
D.矩形的对角线相等且互相平分
3.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( C )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量其中三个角是否都为直角
D.测量对角线是否相等
4.如图,在□ABCD中,对角线AC,BD相交于点O,OA=2,若要使□ABCD为矩形,则OB的长应该为( C )
A.4 B.3 C.2 D.1
(第4题图) (第5题图 ) (第6题图)
5.如图,要使平行四边形ABCD是矩形,则应添加的条件是__∠ABC=90°或AC=BD(答案不唯一)__.(添加一个条件即可)
6.如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为__60__度时,四边形ABFE为矩形.
7.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为__12__.
8.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件BC=2AB _时,四边形PEMF为矩形.
9.已知□ABCD的对角线交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使□ABCD是矩形的条件的序号是__①③④__.
10.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE,求证:四边形BCDE是矩形.
解:证明:∵AC=AB,AD=AE,∠BAD=∠CAE,∴∠CAD=∠BAD-∠CAB=∠CAE-∠CAB=∠BAE.∴△ADC≌△AEB.∴DC=BE,∠ABE=∠ACD.又∵DE=BC,∴四边形BCDE为平行四边形.∵AB=AC,∴∠ABC=ACB,∴∠ABC+∠ABE=∠ACB+∠ACD,即∠EBC=∠DCB=90°.∴四边形BCED为矩形
11.已知,如图,在□ABCD中,对角线AC,BD相交于点O,且△OAB是等边三角形,若□ABCD的面积是16,求对角线AC的长.
解:∵△OAB是等边三角形,∴OA=OB,∠OAB=60°,又∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴AC=BD,∴?ABCD是矩形,∴∠ABC=90°,∵∠OAB=60°,∴∠ACB=30°,∴AC=2AB,BC=AB,∴AB·AB=16,∴AB=4,∴AC=8
12.如图,点E,F分别△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.
(1)求证:四边形ABED是平行四边形;
(2)若AB=AC,求证:四边形AECD是矩形.
解:(1)证明:∵AF=CF,DF=EF,∴四边形AECD是平行四边形,∴AD∥BC,AD=CE,又∵BE=CE,∴AD=BE,∴四边形ABED是平行四边形.
(2)∵AB=AC,BE=CE,∴AE⊥BC,∴∠AEC=90°,∴□ABCD是矩形.
13.如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?请说明理由.
解:(1)证明:∵BE⊥AC,DF⊥AC,∴∠BEO=∠DFO=90°,∵点O是EF的中点,∴OE=OF,又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).
(2)四边形ABCD是矩形.理由如下:∵△BOE≌△DOF,∴OB=OD,又∵OA=OC,∴四边形ABCD是平行四边形,∵OA=BD,OA=AC,∴BD=AC,∴□ABCD是矩形.
14.如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:∵CF平分∠ACD,且MN∥BD,∴∠ACF=∠FCD=∠CFO.∴OF=OC.同理可证:OC=OE.∴OE=OF.
由(1)知:OF=OC,OC=OE,∴∠OCF=∠OFC,∠OCE=∠OEC.∴∠OCF+∠OCE=∠OFC+∠OEC.而∠OCF+∠OCE+∠OFC+∠OEC=180°,∴∠ECF=∠OCF+∠OCE=90°,∴EF===13.∴OC=EF=.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形..理由如下:由(1)知OE=OF, 当点O移动到AC中点时有OA=OC,∴四边形AECF是平行四边形, ∵∠ECF=90°, ∴平行四边形AECF是矩形.
15.(上海)已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( B )
A.∠A=∠B B.∠A=∠C C.AC=B D.AB⊥BC
16.(玉林)如图,在?ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM'与NN',在DC与AB上的垂足分别是M,N与M′,N′,连接EF.求证:四边形EFNM是矩形;
证明:过点E、F分别作AD、BC的垂线,垂足分别是G、H.∵∠3=∠4,∠1=∠2,EG⊥AD,EM⊥CD,EM′⊥AB∴EG=ME,EG=EM′
∴EG=ME=ME′=MM′,
同理可证:FH=NF=N′F=NN′,
∵CD∥AB,MM′⊥CD,NN′⊥CD,
∴MM′=NN′,∴ME=NF=EG=FH,
又∵MM′∥NN′,MM′⊥CD,
∴四边形EFNM是矩形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
