4.4 探索三角形相似的条件同步练习题(含答案)
文档属性
| 名称 | 4.4 探索三角形相似的条件同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览


文档简介
第四章 图形的相似
4 探索三角形相似的条件
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′,∠B=∠B′ B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′ D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
2.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
4.甲三角形的三边分别是1,,,乙三角形的三边分别是5,,,则甲,乙两个三角形是( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
5.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
(第5题图) (第9题图) (第10题图) (第12题图)
6.已知点E是线段MN的黄金分割点(ME>EN),则下列式子正确的是( )
A.= B.= C.= D.=
7.已知线段AB=10 cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( )
A.(5-10) cm B.(15-5) cm C.(5-5) cm D.(10-2) cm
8.把2米的线段进行黄金分割,则分成的较短的线段长为( )
A.(3-)米 B.(-1)米 C.(1+)米 D.(3+)米
9.如图,锐角三角形ABC的边AB和AC边上的高CE和BF相交于点D,请写出图中一对相似三角形__ __.
10.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为 _.
11.已知线段AD,BC相交于点O,OB∶OD=3∶1,OA=12 cm,OC=4 cm,AB=30 cm,则CD= _cm.
12.如图,点D是△ABC边AB上的一点,AD=2BD=2,当AC= _时,△ACD∽△ABC.
13.如图,线段AC与BD相交于点O,且OA=12,OC=54,OD=36,OB=18,则△ABO与△DCO _相似.(填“一定”或“不”)
(第13题图) (第14题图)
14如图,BD平分∠ABC,AB=2,BC=3,当BD= _时,△ABD∽△DBC.
15.一个三角形的边长分别为5 cm,8 cm,12 cm,另一个三角形的最长边为7.2 cm,则当另一个三角形的另外两边长是 _cm时,这两个三角形相似.
16.△ABC的三边长分别为,,2,△A1B1C1的两边长为1,,要使△ABC∽△A1B1C1,那么△A1B1C1的第三边长为 _.
17.当气温与人体正常体温(37 ℃)之比等于黄金分割比0.618时,人体感觉最舒适,这个气温约为 _℃.(取整数)
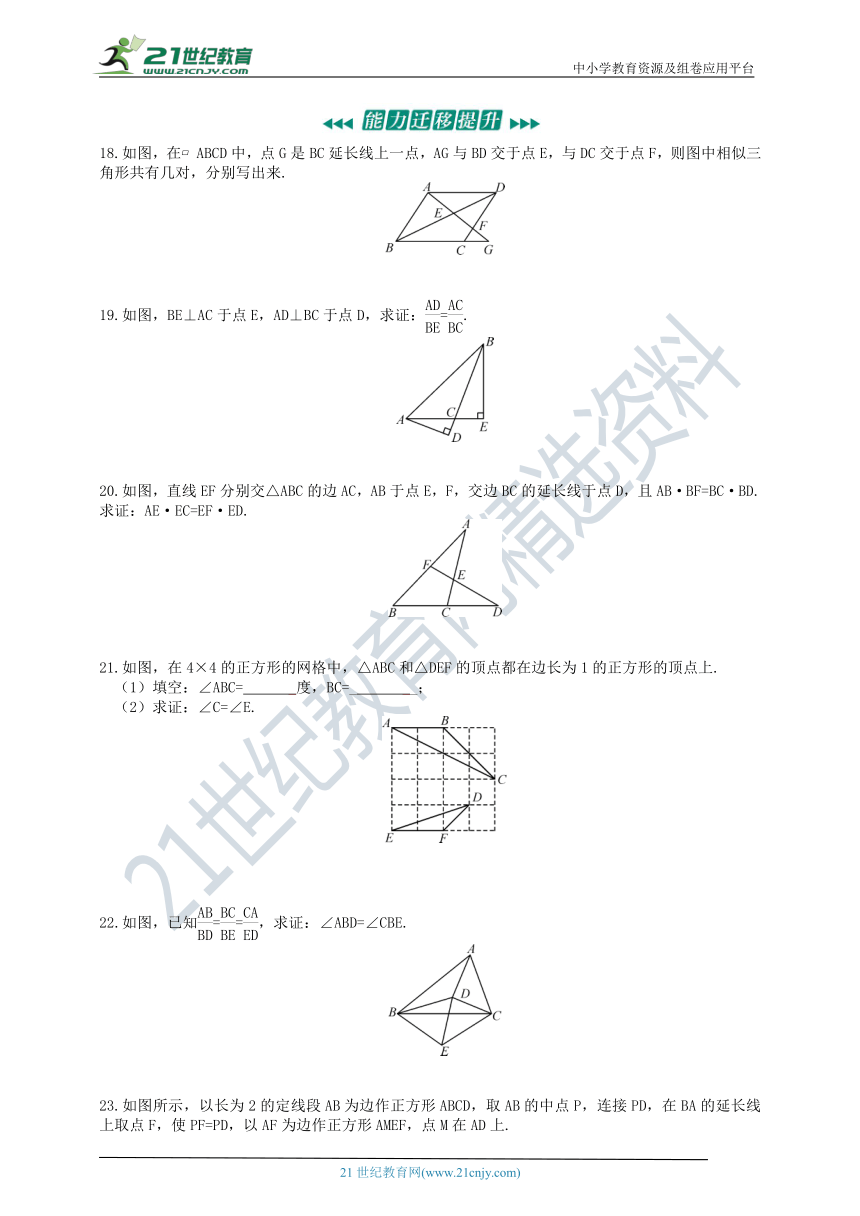
18.如图,在?ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有几对,分别写出来.
19.如图,BE⊥AC于点E,AD⊥BC于点D,求证:=.
20.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB·BF=BC·BD.求证:AE·EC=EF·ED.
21.如图,在4×4的正方形的网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC= _度,BC=_ __;
(2)求证:∠C=∠E.
22.如图,已知==,求证:∠ABD=∠CBE.
23.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
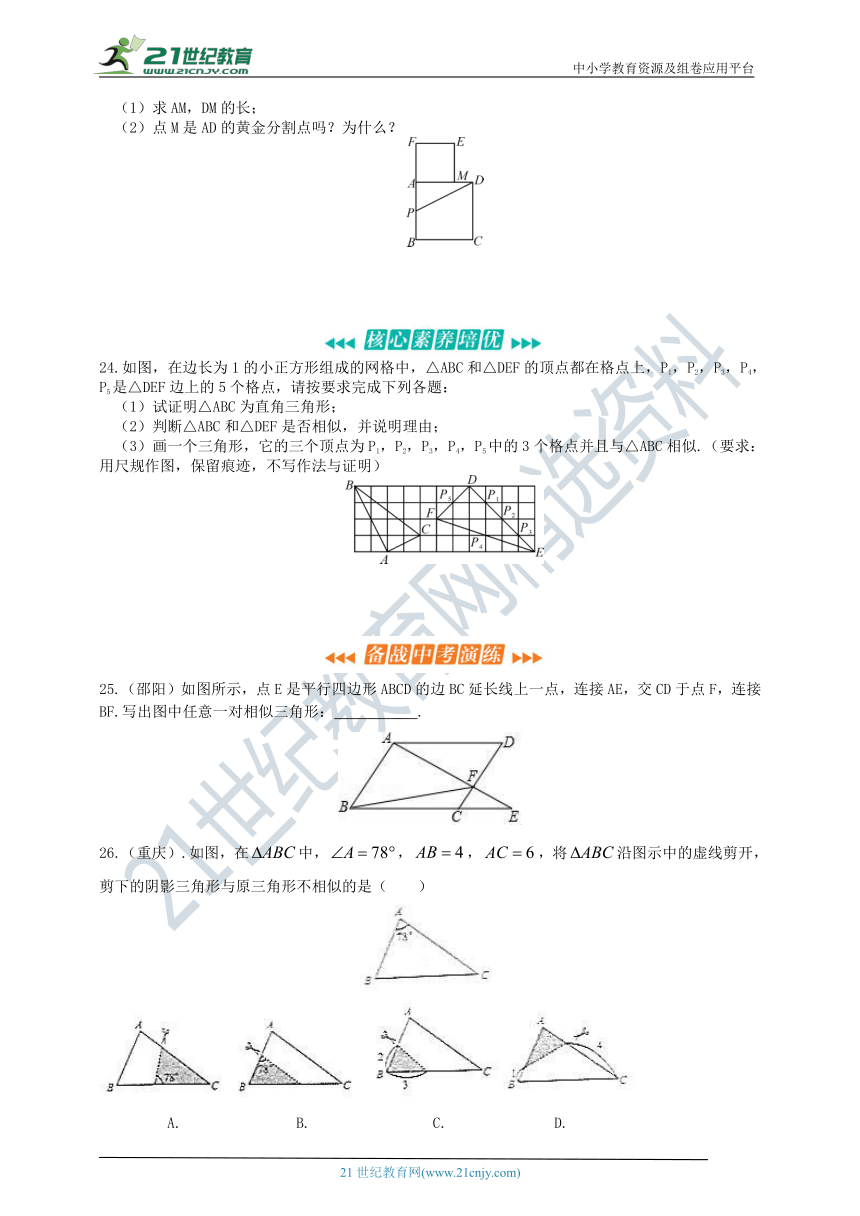
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
24.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似.(要求:用尺规作图,保留痕迹,不写作法与证明)
25.(邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: _ .
26.(重庆).如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C. D.
参考答案
第四章 图形的相似
4 探索三角形相似的条件
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( C )
A.∠A=∠A′,∠B=∠B′ B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′ D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
2.下列各组图形中有可能不相似的是( A )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( C )
4.甲三角形的三边分别是1,,,乙三角形的三边分别是5,,,则甲,乙两个三角形是( A )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
5.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( D )
A.1对 B.2对 C.3对 D.4对
(第5题图) (第9题图) (第10题图) (第12题图)
6.已知点E是线段MN的黄金分割点(ME>EN),则下列式子正确的是( A )
A.= B.= C.= D.=
7.已知线段AB=10 cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( C )
A.(5-10) cm B.(15-5) cm C.(5-5) cm D.(10-2) cm
8.把2米的线段进行黄金分割,则分成的较短的线段长为( A )
A.(3-)米 B.(-1)米 C.(1+)米 D.(3+)米
9.如图,锐角三角形ABC的边AB和AC边上的高CE和BF相交于点D,请写出图中一对相似三角形__△ABF∽△ACE(或△BDE∽△CDF)__.
10.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为____.
11.已知线段AD,BC相交于点O,OB∶OD=3∶1,OA=12 cm,OC=4 cm,AB=30 cm,则CD=__10__cm.
12.如图,点D是△ABC边AB上的一点,AD=2BD=2,当AC=____时,△ACD∽△ABC.
13.如图,线段AC与BD相交于点O,且OA=12,OC=54,OD=36,OB=18,则△ABO与△DCO一定相似.(填“一定”或“不”)
(第13题图) (第14题图)
14如图,BD平分∠ABC,AB=2,BC=3,当BD=____时,△ABD∽△DBC.
15.一个三角形的边长分别为5 cm,8 cm,12 cm,另一个三角形的最长边为7.2 cm,则当另一个三角形的另外两边长是__3和4.8__cm时,这两个三角形相似.
16.△ABC的三边长分别为,,2,△A1B1C1的两边长为1,,要使△ABC∽△A1B1C1,那么△A1B1C1的第三边长为____.
17.当气温与人体正常体温(37 ℃)之比等于黄金分割比0.618时,人体感觉最舒适,这个气温约为__23__℃.(取整数)
18.如图,在?ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有几对,分别写出来.
解:①△ABD∽△CDB;②△ABE∽△FDE;③△AED∽△GEB;④△ABG∽△FCG∽△FDA,所以图形中一共有6对相似三角形.
19.如图,BE⊥AC于点E,AD⊥BC于点D,求证:=.
解:证明:在△ADC与△BEC中,∵AD⊥BC于点D,BE⊥AC于点E,∴∠D=∠E=90°,又∵∠ACD=∠BCE,∴△ACD∽△BCE,∴=.
20.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB·BF=BC·BD.求证:AE·EC=EF·ED.
解:∵AB·BF=BC·BD,∴=.又∵∠B=∠B,∴△ABC∽△DBF.∴∠A=∠D.又∵∠AEF=∠DEC,∴△AEF∽△DEC.∴=,即AE·EC=EF·ED.
21.如图,在4×4的正方形的网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__135__度,BC=__2__;
(2)求证:∠C=∠E.
解:(2)证明:由图知,AB=2,BC=2,AC=2,DF=,EF=2,DE=,∴=,==,==,∴==,∴△DEF∽△ACB,∴∠C=∠E.
22.如图,已知==,求证:∠ABD=∠CBE.
证明:∵==,∴△ABC∽△DBE,∴∠ABC=∠DBE,∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.
23.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
解:(1)∵正方形ABCD的边长是2,点P是AB的中点,∴AB=AD=2,AP=1,∠BAD=90°,∴PD==,∵PF=PD,∴AF=-1.在正方形AMEF中,AM=AF=-1,MD=AD-AM=3-
(2)点M是线段AD的黄金分割点,由(1)得AD·DM=2(3-)=6-2,又AM2=(-1)2=6-2,∴AM2=AD·DM.
24.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似.(要求:用尺规作图,保留痕迹,不写作法与证明)
解:(1)由题意得AB=2,AC=,BC=5,∵AB2+AC2=BC2,∴△ABC为直角三角形.
(2)△ABC与△DEF相似,理由如下:由勾股定理,得DE=4,DF=2,EF=2,则===,∴△ABC∽△DEF.
(3)连接P2P5,P2P4,P4P5,在△P4P5P2中,∵P2P5=,P4P5=2,P2P4=,∴===,∴△ABC∽△P4P5P2.
25.(邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: △ADF∽△ECF .
26.(重庆).如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( C )
A. B. C. D.
4 探索三角形相似的条件
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( )
A.∠A=∠A′,∠B=∠B′ B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′ D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
2.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
4.甲三角形的三边分别是1,,,乙三角形的三边分别是5,,,则甲,乙两个三角形是( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
5.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )
A.1对 B.2对 C.3对 D.4对
(第5题图) (第9题图) (第10题图) (第12题图)
6.已知点E是线段MN的黄金分割点(ME>EN),则下列式子正确的是( )
A.= B.= C.= D.=
7.已知线段AB=10 cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( )
A.(5-10) cm B.(15-5) cm C.(5-5) cm D.(10-2) cm
8.把2米的线段进行黄金分割,则分成的较短的线段长为( )
A.(3-)米 B.(-1)米 C.(1+)米 D.(3+)米
9.如图,锐角三角形ABC的边AB和AC边上的高CE和BF相交于点D,请写出图中一对相似三角形__ __.
10.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为 _.
11.已知线段AD,BC相交于点O,OB∶OD=3∶1,OA=12 cm,OC=4 cm,AB=30 cm,则CD= _cm.
12.如图,点D是△ABC边AB上的一点,AD=2BD=2,当AC= _时,△ACD∽△ABC.
13.如图,线段AC与BD相交于点O,且OA=12,OC=54,OD=36,OB=18,则△ABO与△DCO _相似.(填“一定”或“不”)
(第13题图) (第14题图)
14如图,BD平分∠ABC,AB=2,BC=3,当BD= _时,△ABD∽△DBC.
15.一个三角形的边长分别为5 cm,8 cm,12 cm,另一个三角形的最长边为7.2 cm,则当另一个三角形的另外两边长是 _cm时,这两个三角形相似.
16.△ABC的三边长分别为,,2,△A1B1C1的两边长为1,,要使△ABC∽△A1B1C1,那么△A1B1C1的第三边长为 _.
17.当气温与人体正常体温(37 ℃)之比等于黄金分割比0.618时,人体感觉最舒适,这个气温约为 _℃.(取整数)
18.如图,在?ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有几对,分别写出来.
19.如图,BE⊥AC于点E,AD⊥BC于点D,求证:=.
20.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB·BF=BC·BD.求证:AE·EC=EF·ED.
21.如图,在4×4的正方形的网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC= _度,BC=_ __;
(2)求证:∠C=∠E.
22.如图,已知==,求证:∠ABD=∠CBE.
23.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
24.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似.(要求:用尺规作图,保留痕迹,不写作法与证明)
25.(邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: _ .
26.(重庆).如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C. D.
参考答案
第四章 图形的相似
4 探索三角形相似的条件
1.下列各组条件,不能判定△ABC与△A′B′C′相似的是( C )
A.∠A=∠A′,∠B=∠B′ B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′ D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
2.下列各组图形中有可能不相似的是( A )
A.各有一个角是45°的两个等腰三角形 B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形 D.两个等腰直角三角形
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( C )
4.甲三角形的三边分别是1,,,乙三角形的三边分别是5,,,则甲,乙两个三角形是( A )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
5.如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( D )
A.1对 B.2对 C.3对 D.4对
(第5题图) (第9题图) (第10题图) (第12题图)
6.已知点E是线段MN的黄金分割点(ME>EN),则下列式子正确的是( A )
A.= B.= C.= D.=
7.已知线段AB=10 cm,点C是线段AB的黄金分割点(AC>BC),则AC的长为( C )
A.(5-10) cm B.(15-5) cm C.(5-5) cm D.(10-2) cm
8.把2米的线段进行黄金分割,则分成的较短的线段长为( A )
A.(3-)米 B.(-1)米 C.(1+)米 D.(3+)米
9.如图,锐角三角形ABC的边AB和AC边上的高CE和BF相交于点D,请写出图中一对相似三角形__△ABF∽△ACE(或△BDE∽△CDF)__.
10.如图,在矩形ABCD中,AB=2,BC=1,点E是DC上一点,∠DAE=∠BAC,则EC的长为____.
11.已知线段AD,BC相交于点O,OB∶OD=3∶1,OA=12 cm,OC=4 cm,AB=30 cm,则CD=__10__cm.
12.如图,点D是△ABC边AB上的一点,AD=2BD=2,当AC=____时,△ACD∽△ABC.
13.如图,线段AC与BD相交于点O,且OA=12,OC=54,OD=36,OB=18,则△ABO与△DCO一定相似.(填“一定”或“不”)
(第13题图) (第14题图)
14如图,BD平分∠ABC,AB=2,BC=3,当BD=____时,△ABD∽△DBC.
15.一个三角形的边长分别为5 cm,8 cm,12 cm,另一个三角形的最长边为7.2 cm,则当另一个三角形的另外两边长是__3和4.8__cm时,这两个三角形相似.
16.△ABC的三边长分别为,,2,△A1B1C1的两边长为1,,要使△ABC∽△A1B1C1,那么△A1B1C1的第三边长为____.
17.当气温与人体正常体温(37 ℃)之比等于黄金分割比0.618时,人体感觉最舒适,这个气温约为__23__℃.(取整数)
18.如图,在?ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,则图中相似三角形共有几对,分别写出来.
解:①△ABD∽△CDB;②△ABE∽△FDE;③△AED∽△GEB;④△ABG∽△FCG∽△FDA,所以图形中一共有6对相似三角形.
19.如图,BE⊥AC于点E,AD⊥BC于点D,求证:=.
解:证明:在△ADC与△BEC中,∵AD⊥BC于点D,BE⊥AC于点E,∴∠D=∠E=90°,又∵∠ACD=∠BCE,∴△ACD∽△BCE,∴=.
20.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB·BF=BC·BD.求证:AE·EC=EF·ED.
解:∵AB·BF=BC·BD,∴=.又∵∠B=∠B,∴△ABC∽△DBF.∴∠A=∠D.又∵∠AEF=∠DEC,∴△AEF∽△DEC.∴=,即AE·EC=EF·ED.
21.如图,在4×4的正方形的网格中,△ABC和△DEF的顶点都在边长为1的正方形的顶点上.
(1)填空:∠ABC=__135__度,BC=__2__;
(2)求证:∠C=∠E.
解:(2)证明:由图知,AB=2,BC=2,AC=2,DF=,EF=2,DE=,∴=,==,==,∴==,∴△DEF∽△ACB,∴∠C=∠E.
22.如图,已知==,求证:∠ABD=∠CBE.
证明:∵==,∴△ABC∽△DBE,∴∠ABC=∠DBE,∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE.
23.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)点M是AD的黄金分割点吗?为什么?
解:(1)∵正方形ABCD的边长是2,点P是AB的中点,∴AB=AD=2,AP=1,∠BAD=90°,∴PD==,∵PF=PD,∴AF=-1.在正方形AMEF中,AM=AF=-1,MD=AD-AM=3-
(2)点M是线段AD的黄金分割点,由(1)得AD·DM=2(3-)=6-2,又AM2=(-1)2=6-2,∴AM2=AD·DM.
24.如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)画一个三角形,它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC相似.(要求:用尺规作图,保留痕迹,不写作法与证明)
解:(1)由题意得AB=2,AC=,BC=5,∵AB2+AC2=BC2,∴△ABC为直角三角形.
(2)△ABC与△DEF相似,理由如下:由勾股定理,得DE=4,DF=2,EF=2,则===,∴△ABC∽△DEF.
(3)连接P2P5,P2P4,P4P5,在△P4P5P2中,∵P2P5=,P4P5=2,P2P4=,∴===,∴△ABC∽△P4P5P2.
25.(邵阳)如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: △ADF∽△ECF .
26.(重庆).如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( C )
A. B. C. D.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
