6.4 数据的离散程度同步练习题(含答案)
文档属性
| 名称 | 6.4 数据的离散程度同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 20:44:05 | ||
图片预览


文档简介
第六章 数据的分析
4 数据的离散程度
/
1.样本方差的作用是( )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
2.一个样本的方差是0,若中位数是,那么它的平均数是( )
A.等于 B.不等于 C.大于 D.小于
3.已知样本数据101,98,102,100,99,则这个样本的标准差是( )
A.0 B.1 C. D.2
4.如果给定数组中每一个数都减去同一非零常数,则数据的( )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 A、平均数不变,方差改变
5.如图是甲、两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( )
A.甲 B.乙 C.甲、乙的成绩一样稳定;D.无法确定
/
6.人数相等的甲。乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
7.下列统计量中,能反映一名同学在7~9 年级学段的学习成绩稳定程度的是 ( )
A.平均数 B.中位数 C.众数 D.方差
8.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2, 3,1,2则在这10天中该车间生产零件的次品数的( )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
9.在甲、乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
10.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为_______cm。
11.五个数1,2,4,5,a的平均数是3,则a= ,这五个数的方差为 。
12.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 ,中位数为 ,方差为 。
13.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是____环,中位数____环,方差是______。
14.已知数据a。b。c的方差是1,则4a,4b,4c的方差是 。
/
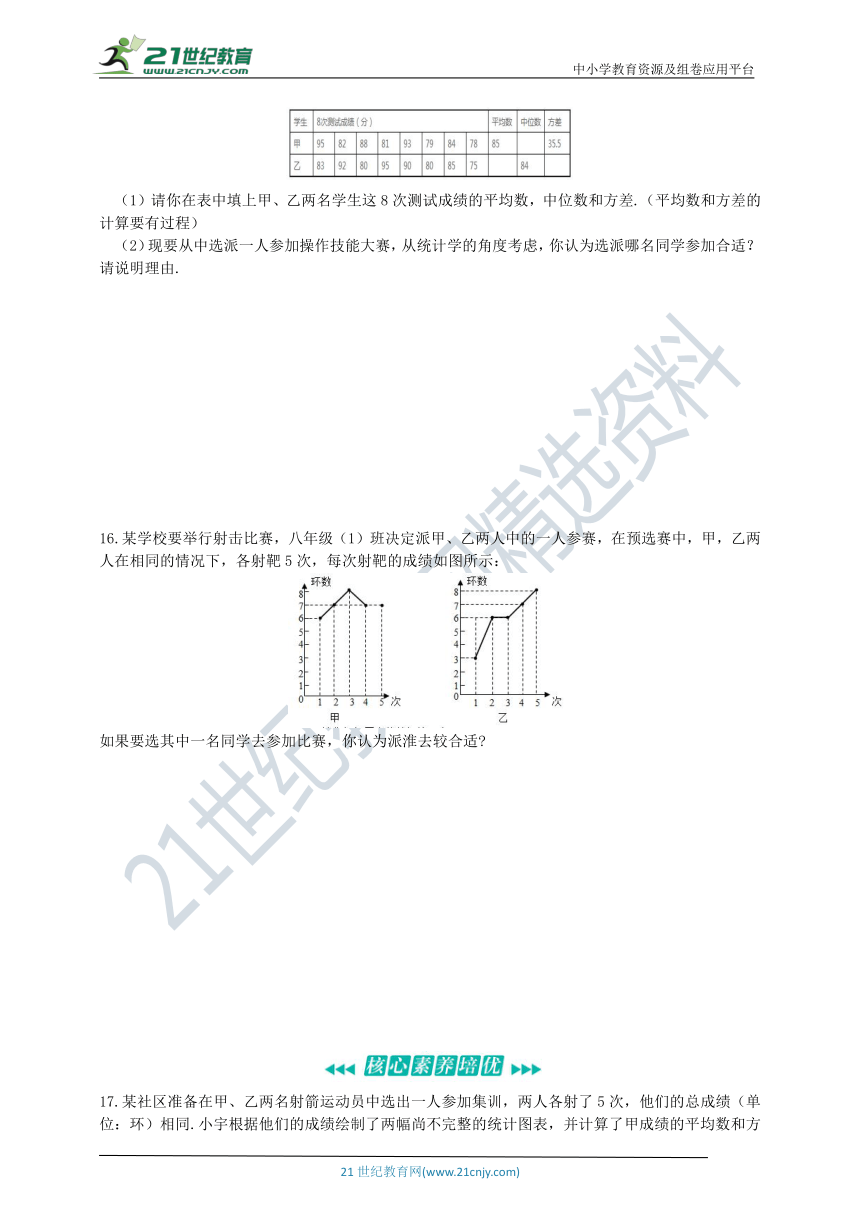
15.铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
16.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
/
17.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
/
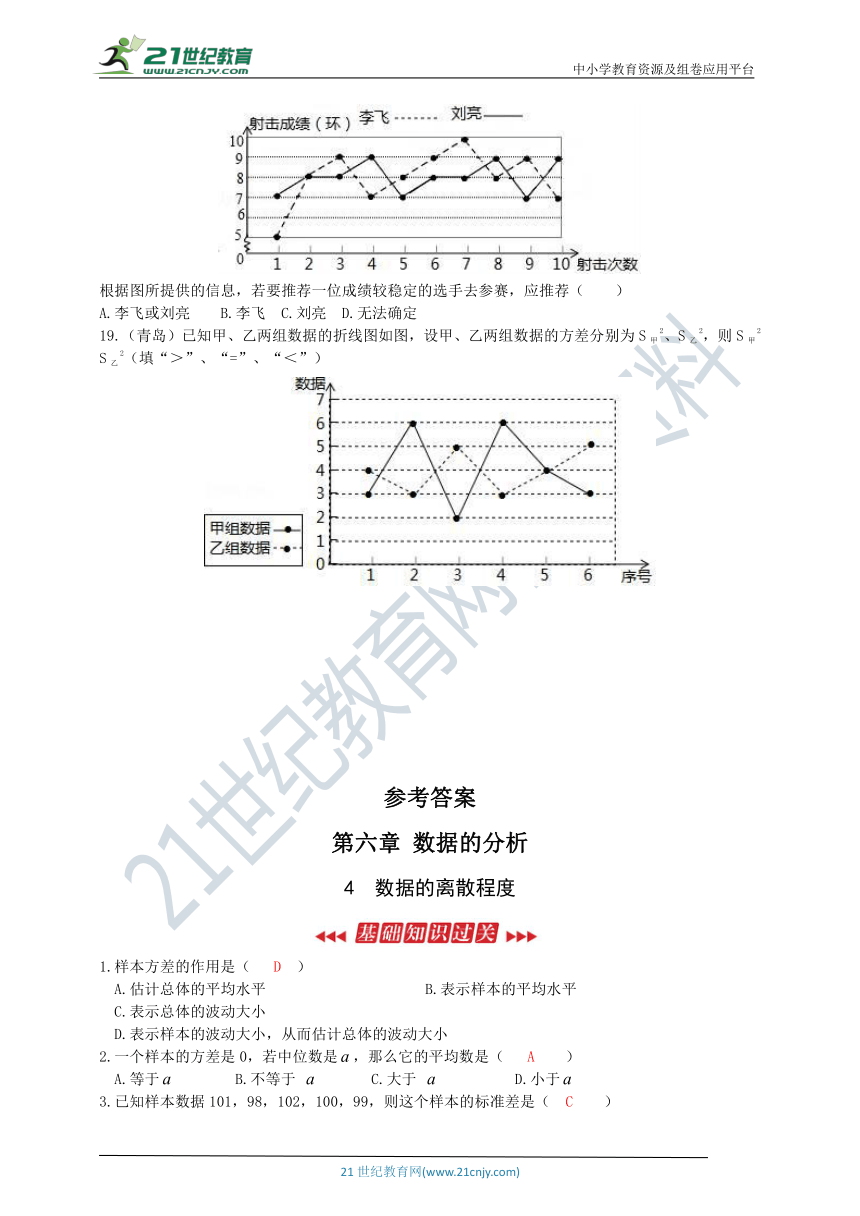
18.(邵阳)根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
/
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
19.(青岛)已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S甲2、S乙2,则S甲2 S乙2(填“>”、“=”、“<”)
/
参考答案
第六章 数据的分析
4 数据的离散程度
/
1.样本方差的作用是( D )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
2.一个样本的方差是0,若中位数是,那么它的平均数是( A )
A.等于 B.不等于 C.大于 D.小于
3.已知样本数据101,98,102,100,99,则这个样本的标准差是( C )
A.0 B.1 C. D.2
4.如果给定数组中每一个数都减去同一非零常数,则数据的( A )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 A、平均数不变,方差改变
5.如图是甲、两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( A )
A.甲 B.乙 C.甲、乙的成绩一样稳定;D.无法确定
/
6.人数相等的甲。乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( B )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
7.下列统计量中,能反映一名同学在7~9 年级学段的学习成绩稳定程度的是 ( D )
A.平均数 B.中位数 C.众数 D.方差
8.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2, 3,1,2则在这10天中该车间生产零件的次品数的( C )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
9.在甲、乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( B )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
10.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为____4___cm。
11.五个数1,2,4,5,a的平均数是3,则a= 3 ,这五个数的方差为 2 。
12.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 0 ,中位数为 0 ,方差为 1.5 。
13.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是_8___环,中位数__8__环,方差是___2___。
14.已知数据a。b。c的方差是1,则4a,4b,4c的方差是 16 。
/
15.铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
.解:(1)甲的成绩从小到大排列为78,79,81,82,84,88,93,95,则甲成绩的中位数为=83(分).
乙的平均数为=85(分),
乙成绩的方差为
=41.
(2)选派甲同学参加合适.理由:从平均数上看甲、乙相同,说明甲、乙的实力相当,但是甲的方差比乙小,说明甲的成绩比乙稳定,因此选派甲同学参加合适.
16.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
解:派甲参赛.
甲=×(6+7+8+7+7)=7(环),
乙=×(3+6+6+7+8)=6(环),
s2甲=×[(6-7)2+(7-7)2+(8-7)2+(7-7)2+(7-7)2]=,
s2乙=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=.
因为甲>乙,且s2甲/
17.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
解:(1)4 6
(2)如如所示:
/
(3)乙的成绩比较稳定.
乙=×(7+5+7+4+7)=6(环),
s2乙=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(5-6)2]=1.6.
∵甲=乙,s2乙∴乙的成绩比较稳定,将被选中.
/
18.(邵阳)根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
/
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( C )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
19.(青岛)已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S甲2、S乙2,则S甲2 > S乙2(填“>”、“=”、“<”)
/
/
4 数据的离散程度
/
1.样本方差的作用是( )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
2.一个样本的方差是0,若中位数是,那么它的平均数是( )
A.等于 B.不等于 C.大于 D.小于
3.已知样本数据101,98,102,100,99,则这个样本的标准差是( )
A.0 B.1 C. D.2
4.如果给定数组中每一个数都减去同一非零常数,则数据的( )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 A、平均数不变,方差改变
5.如图是甲、两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( )
A.甲 B.乙 C.甲、乙的成绩一样稳定;D.无法确定
/
6.人数相等的甲。乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
7.下列统计量中,能反映一名同学在7~9 年级学段的学习成绩稳定程度的是 ( )
A.平均数 B.中位数 C.众数 D.方差
8.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2, 3,1,2则在这10天中该车间生产零件的次品数的( )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
9.在甲、乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
10.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为_______cm。
11.五个数1,2,4,5,a的平均数是3,则a= ,这五个数的方差为 。
12.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 ,中位数为 ,方差为 。
13.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是____环,中位数____环,方差是______。
14.已知数据a。b。c的方差是1,则4a,4b,4c的方差是 。
/
15.铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
16.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
/
17.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
/
18.(邵阳)根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
/
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
19.(青岛)已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S甲2、S乙2,则S甲2 S乙2(填“>”、“=”、“<”)
/
参考答案
第六章 数据的分析
4 数据的离散程度
/
1.样本方差的作用是( D )
A.估计总体的平均水平 B.表示样本的平均水平
C.表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
2.一个样本的方差是0,若中位数是,那么它的平均数是( A )
A.等于 B.不等于 C.大于 D.小于
3.已知样本数据101,98,102,100,99,则这个样本的标准差是( C )
A.0 B.1 C. D.2
4.如果给定数组中每一个数都减去同一非零常数,则数据的( A )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 A、平均数不变,方差改变
5.如图是甲、两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( A )
A.甲 B.乙 C.甲、乙的成绩一样稳定;D.无法确定
/
6.人数相等的甲。乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( B )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
7.下列统计量中,能反映一名同学在7~9 年级学段的学习成绩稳定程度的是 ( D )
A.平均数 B.中位数 C.众数 D.方差
8.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2, 3,1,2则在这10天中该车间生产零件的次品数的( C )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
9.在甲、乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( B )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
10.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为____4___cm。
11.五个数1,2,4,5,a的平均数是3,则a= 3 ,这五个数的方差为 2 。
12.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 0 ,中位数为 0 ,方差为 1.5 。
13.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是_8___环,中位数__8__环,方差是___2___。
14.已知数据a。b。c的方差是1,则4a,4b,4c的方差是 16 。
/
15.铜陵职业技术学院甲、乙两名学生参加操作技能培训.从他们在培训期间参加的多次测试成绩中随机抽取8次,记录如下:
/
(1)请你在表中填上甲、乙两名学生这8次测试成绩的平均数,中位数和方差.(平均数和方差的计算要有过程)
(2)现要从中选派一人参加操作技能大赛,从统计学的角度考虑,你认为选派哪名同学参加合适?请说明理由.
.解:(1)甲的成绩从小到大排列为78,79,81,82,84,88,93,95,则甲成绩的中位数为=83(分).
乙的平均数为=85(分),
乙成绩的方差为
=41.
(2)选派甲同学参加合适.理由:从平均数上看甲、乙相同,说明甲、乙的实力相当,但是甲的方差比乙小,说明甲的成绩比乙稳定,因此选派甲同学参加合适.
16.某学校要举行射击比赛,八年级(1)班决定派甲、乙两人中的一人参赛,在预选赛中,甲,乙两人在相同的情况下,各射靶5次,每次射靶的成绩如图所示:
/
如果要选其中一名同学去参加比赛,你认为派淮去较合适?
解:派甲参赛.
甲=×(6+7+8+7+7)=7(环),
乙=×(3+6+6+7+8)=6(环),
s2甲=×[(6-7)2+(7-7)2+(8-7)2+(7-7)2+(7-7)2]=,
s2乙=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=.
因为甲>乙,且s2甲
17.某社区准备在甲、乙两名射箭运动员中选出一人参加集训,两人各射了5次,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了两幅尚不完整的统计图表,并计算了甲成绩的平均数和方差.
/
//
(1)a= ,甲= .
(2)补全图中表示乙变化情况的折线图.
(3)观察折线统计图,可看出成绩比较稳定的是谁?参照小字的计算方法,计算乙成绩的方差,并判断谁将被选中.
解:(1)4 6
(2)如如所示:
/
(3)乙的成绩比较稳定.
乙=×(7+5+7+4+7)=6(环),
s2乙=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(5-6)2]=1.6.
∵甲=乙,s2乙
/
18.(邵阳)根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
/
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( C )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
19.(青岛)已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S甲2、S乙2,则S甲2 > S乙2(填“>”、“=”、“<”)
/
/
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
