7.5 三角形内角和定理同步练习题(含答案)
文档属性
| 名称 | 7.5 三角形内角和定理同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 20:52:11 | ||
图片预览



文档简介
第七章 平行线的证明
5 三角形内角和定理
/
1.若一个三角形三个内角度数的比为2:7:4,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
3.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( )
A.50° B.45° C.55° D.40°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
///
(第5题图) (第6题图) (第7题图)
A.40° B.54° C.45° D.50°
5.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
A.360° B.250° C.180° D.140°
6.关于三角形内角的叙述错误的是( )
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
7.如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
A.95° B.120° C.135° D.无法确定
8.三角形中,最大角等于最小角的2倍,最大角又比另一个角大20°,则此三角形的最小角等于 .
9.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠ ,∠C=∠ .
////
(第9题图) (第10题图) (第11题图) (第12题图)
10.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为 度.
11.如图,∠α= .
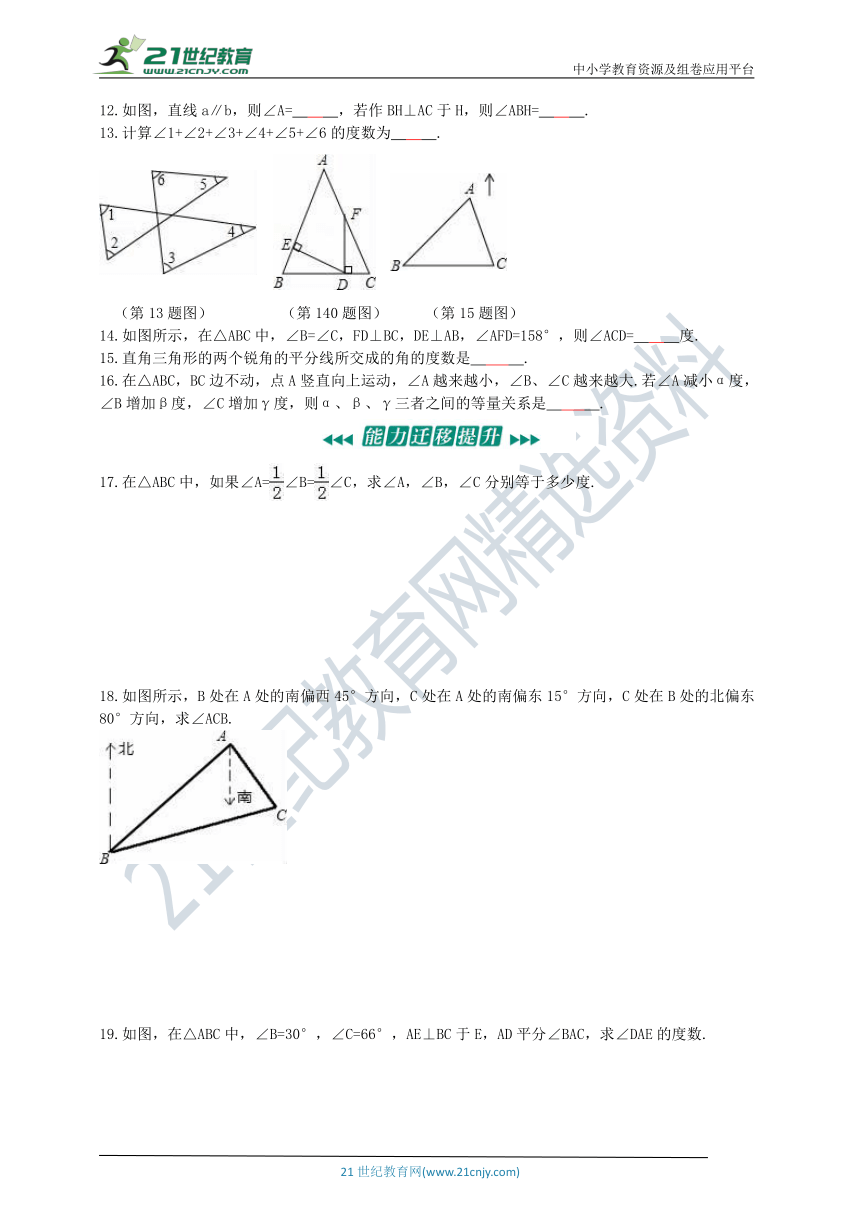
12.如图,直线a∥b,则∠A= ,若作BH⊥AC于H,则∠ABH= .
13.计算∠1+∠2+∠3+∠4+∠5+∠6的度数为 .
/ / /
(第13题图) (第140题图) (第15题图)
14.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠ACD= 度.
15.直角三角形的两个锐角的平分线所交成的角的度数是 .
16.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
/
17.在△ABC中,如果∠A=/∠B=/∠C,求∠A,∠B,∠C分别等于多少度.
18.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
/
19.如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.
/
20.如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.
/
/
21.如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
/
/
22.(临沂)如图,AB∥CD,∠D=42°,∠CBA=64°,则∠CBD的度数是( )
/
A.42° B.64° C.74° D.106°
23.(孝感)如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
/
A.42° B.50° C.60° D.68°
参考答案
第七章 平行线的证明
5 三角形内角和定理
/
1.若一个三角形三个内角度数的比为2:7:4,那么这个三角形是( C )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( C )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
3.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( B )
A.50° B.45° C.55° D.40°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( A )
///
(第5题图) (第6题图) (第7题图)
A.40° B.54° C.45° D.50°
5.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( B )
A.360° B.250° C.180° D.140°
6.关于三角形内角的叙述错误的是( B )
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
7.如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( C )
A.95° B.120° C.135° D.无法确定
8.三角形中,最大角等于最小角的2倍,最大角又比另一个角大20°,则此三角形的最小角等于 40° .
9.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠ DAC ,∠C=∠ BAD .
////
(第9题图) (第10题图) (第11题图) (第12题图)
10.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为 85 度.
11.如图,∠α= 17° .
12.如图,直线a∥b,则∠A= 20° ,若作BH⊥AC于H,则∠ABH= 70° .
13.计算∠1+∠2+∠3+∠4+∠5+∠6的度数为 360° .
/ / /
(第13题图) (第140题图) (第15题图)
14.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠ACD= 68 度.
15.直角三角形的两个锐角的平分线所交成的角的度数是 45°或135° .
16.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 α=β+γ .
/
17.在△ABC中,如果∠A=/∠B=/∠C,求∠A,∠B,∠C分别等于多少度.
解:∵∠A=/∠B=/∠C,
∴∠B=∠C=2∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+2∠A=180°,
解得:∠A=36°,
∴∠B=∠C=72°.
18.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
/
解:∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=45°,
∴∠BAE=∠DBA=45°,
∵∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°,
又∵∠DBC=80°,
∴∠ABC=80°﹣45°=35°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣60°﹣35°=85°.
/
19.如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.
/
解:在△ABC中,∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣30°﹣66°=84°,
∵AD平分∠BAC,
∴∠DAC=/∠BAC=42°,
∵AE⊥BC于E,
∴∠AEC=90°,
∴∠EAC=90°﹣∠C=90°﹣66°=24°,
∴∠DAE=∠DAC﹣∠EAC=42°﹣24°=18°.
20.如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.
/
证明:∵AB∥DE,
∴∠B+∠E=180°,
∵∠B+∠A+∠BCA=180°,∠E+∠D+∠DCE=180°,
∴,∠A+∠BCA+∠D+∠DCE=180°,
∵∠A=∠BCA,∠D=∠DCE,
∴∠ACB+∠DCE=90°,
∴∠ACD=90°,
∴AC⊥CD.
/
21.如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
/
解:(1)∵∠A=30°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣30°=150°,
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=150°﹣90°=60°;
(2)∠ABX+∠ACX的大小没有变化;理由如下:
∵∠ABC+∠ACB=180°﹣∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=180°﹣∠A﹣90°=90°﹣∠A;
即∠ABX+∠ACX的大小没有变化.
/
22.(临沂)如图,AB∥CD,∠D=42°,∠CBA=64°,则∠CBD的度数是( C )
/
A.42° B.64° C.74° D.106°
23.(孝感)如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( C )
/
A.42° B.50° C.60° D.68°
/
5 三角形内角和定理
/
1.若一个三角形三个内角度数的比为2:7:4,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
3.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( )
A.50° B.45° C.55° D.40°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
///
(第5题图) (第6题图) (第7题图)
A.40° B.54° C.45° D.50°
5.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( )
A.360° B.250° C.180° D.140°
6.关于三角形内角的叙述错误的是( )
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
7.如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( )
A.95° B.120° C.135° D.无法确定
8.三角形中,最大角等于最小角的2倍,最大角又比另一个角大20°,则此三角形的最小角等于 .
9.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠ ,∠C=∠ .
////
(第9题图) (第10题图) (第11题图) (第12题图)
10.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为 度.
11.如图,∠α= .
12.如图,直线a∥b,则∠A= ,若作BH⊥AC于H,则∠ABH= .
13.计算∠1+∠2+∠3+∠4+∠5+∠6的度数为 .
/ / /
(第13题图) (第140题图) (第15题图)
14.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠ACD= 度.
15.直角三角形的两个锐角的平分线所交成的角的度数是 .
16.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 .
/
17.在△ABC中,如果∠A=/∠B=/∠C,求∠A,∠B,∠C分别等于多少度.
18.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
/
19.如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.
/
20.如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.
/
/
21.如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
/
/
22.(临沂)如图,AB∥CD,∠D=42°,∠CBA=64°,则∠CBD的度数是( )
/
A.42° B.64° C.74° D.106°
23.(孝感)如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
/
A.42° B.50° C.60° D.68°
参考答案
第七章 平行线的证明
5 三角形内角和定理
/
1.若一个三角形三个内角度数的比为2:7:4,那么这个三角形是( C )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
2.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( C )
A.一定有一个内角为45° B.一定有一个内角为60°
C.一定是直角三角形 D.一定是钝角三角形
3.在△ABC中,∠A﹣∠B=35°,∠C=55°,则∠B等于( B )
A.50° B.45° C.55° D.40°
4.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( A )
///
(第5题图) (第6题图) (第7题图)
A.40° B.54° C.45° D.50°
5.如图,△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2=( B )
A.360° B.250° C.180° D.140°
6.关于三角形内角的叙述错误的是( B )
A.三角形三个内角的和是180°
B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°
D.一个三角形中最大的角所对的边最长
7.如图,点O是△ABC内一点,∠A=80°,∠1=15°,∠2=40°,则∠BOC等于( C )
A.95° B.120° C.135° D.无法确定
8.三角形中,最大角等于最小角的2倍,最大角又比另一个角大20°,则此三角形的最小角等于 40° .
9.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠ DAC ,∠C=∠ BAD .
////
(第9题图) (第10题图) (第11题图) (第12题图)
10.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为 85 度.
11.如图,∠α= 17° .
12.如图,直线a∥b,则∠A= 20° ,若作BH⊥AC于H,则∠ABH= 70° .
13.计算∠1+∠2+∠3+∠4+∠5+∠6的度数为 360° .
/ / /
(第13题图) (第140题图) (第15题图)
14.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠ACD= 68 度.
15.直角三角形的两个锐角的平分线所交成的角的度数是 45°或135° .
16.在△ABC,BC边不动,点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减小α度,∠B增加β度,∠C增加γ度,则α、β、γ三者之间的等量关系是 α=β+γ .
/
17.在△ABC中,如果∠A=/∠B=/∠C,求∠A,∠B,∠C分别等于多少度.
解:∵∠A=/∠B=/∠C,
∴∠B=∠C=2∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+2∠A=180°,
解得:∠A=36°,
∴∠B=∠C=72°.
18.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
/
解:∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=45°,
∴∠BAE=∠DBA=45°,
∵∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°,
又∵∠DBC=80°,
∴∠ABC=80°﹣45°=35°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣60°﹣35°=85°.
/
19.如图,在△ABC中,∠B=30°,∠C=66°,AE⊥BC于E,AD平分∠BAC,求∠DAE的度数.
/
解:在△ABC中,∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣30°﹣66°=84°,
∵AD平分∠BAC,
∴∠DAC=/∠BAC=42°,
∵AE⊥BC于E,
∴∠AEC=90°,
∴∠EAC=90°﹣∠C=90°﹣66°=24°,
∴∠DAE=∠DAC﹣∠EAC=42°﹣24°=18°.
20.如图,已知AB∥DE,点C是BE上的一点,∠A=∠BCA,∠D=∠DCE.求证:AC⊥CD.
/
证明:∵AB∥DE,
∴∠B+∠E=180°,
∵∠B+∠A+∠BCA=180°,∠E+∠D+∠DCE=180°,
∴,∠A+∠BCA+∠D+∠DCE=180°,
∵∠A=∠BCA,∠D=∠DCE,
∴∠ACB+∠DCE=90°,
∴∠ACD=90°,
∴AC⊥CD.
/
21.如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
/
解:(1)∵∠A=30°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣30°=150°,
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=150°﹣90°=60°;
(2)∠ABX+∠ACX的大小没有变化;理由如下:
∵∠ABC+∠ACB=180°﹣∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=180°﹣∠A﹣90°=90°﹣∠A;
即∠ABX+∠ACX的大小没有变化.
/
22.(临沂)如图,AB∥CD,∠D=42°,∠CBA=64°,则∠CBD的度数是( C )
/
A.42° B.64° C.74° D.106°
23.(孝感)如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( C )
/
A.42° B.50° C.60° D.68°
/
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
