3.5 探索与表达规律同步练习题(含答案)
文档属性
| 名称 | 3.5 探索与表达规律同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 22:22:02 | ||
图片预览



文档简介
第三章 整式及其加减
5 探索与表达规律
/
1.找出一列数2,3,5,8,13,□,34的规律,在□里的数应为( )
A.20 B.21 C.22 D.24
2.在一列数1,2,3,4,…,200中,数字“0”出现的次数是( )
A.30 B.31 C.32 D.33
3.观察下列各数:1,, , ,….则这列数的第6个数为( )
A. B. C. D.
4.观察下列图形,则第n个图形中三角形的个数是( )
/
A.2n+2 B.4n+4 C.4n﹣4 D.4n
5.用菱形纸片按规律依次拼成如图所示的图案.第1个图案中有5张菱形纸片;第2个图案中有9张菱形纸片;第3个图案中有13张菱形纸片.按此规律,第6个图案中的菱形纸片的张数为( )
/
A.21 B.23 C.25 D.29
6./ , ……,若 / 符合前面式子的规律, 则a+b = __ __.
7.观察如下图形,按照这种方式摆下去,第(n)个图形需用 枚棋子.
/
8.如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想,然后填空:当黑色瓷砖为20块时,白色瓷砖为____块;白色瓷砖为(为正整数)块时,黑色瓷砖为_____块.
/
/
9.将从1开始的自然数,按如图所示的规律排列,在2,3,5,7,10,13,17,…,处分别拐第1,2,3,4,5,6,7,…,次弯,则第33次拐弯处的那个数是( )
/
A.290 B.226 C.272 D.302
10.如图,在日历中,任意圈出一竖列上相邻的三个数,设中间的数为a,则这三个数之和为 .
/
11.从2开始,连续的偶数相加,和的情况如下表:
加数的个数(n)
和(s)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
….
….
n个从2开始的连续偶数相加时,它们的和S与n之间有什么样的关系?用公式表示出来,并由此计算下列各题:
(1)2+4+6+8+…+202; (2)126+128+130+…+300.
12.用如图形状的三角形砖,按一定的方式搭起一个金字塔:
/
(1)观察图形,并填空:当金字塔分别搭到3层、4层、5层时,所用三角形砖的块数分别为: 、 、 ,又推断,当金字塔搭了n层时共用去三角形砖 块;
(2)试推断,当金字塔搭到第99层时,底层需要多少三角形砖块;反之,若底层用了99块三角形砖时,则金字塔能搭几层?
/
13.将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
/
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
/
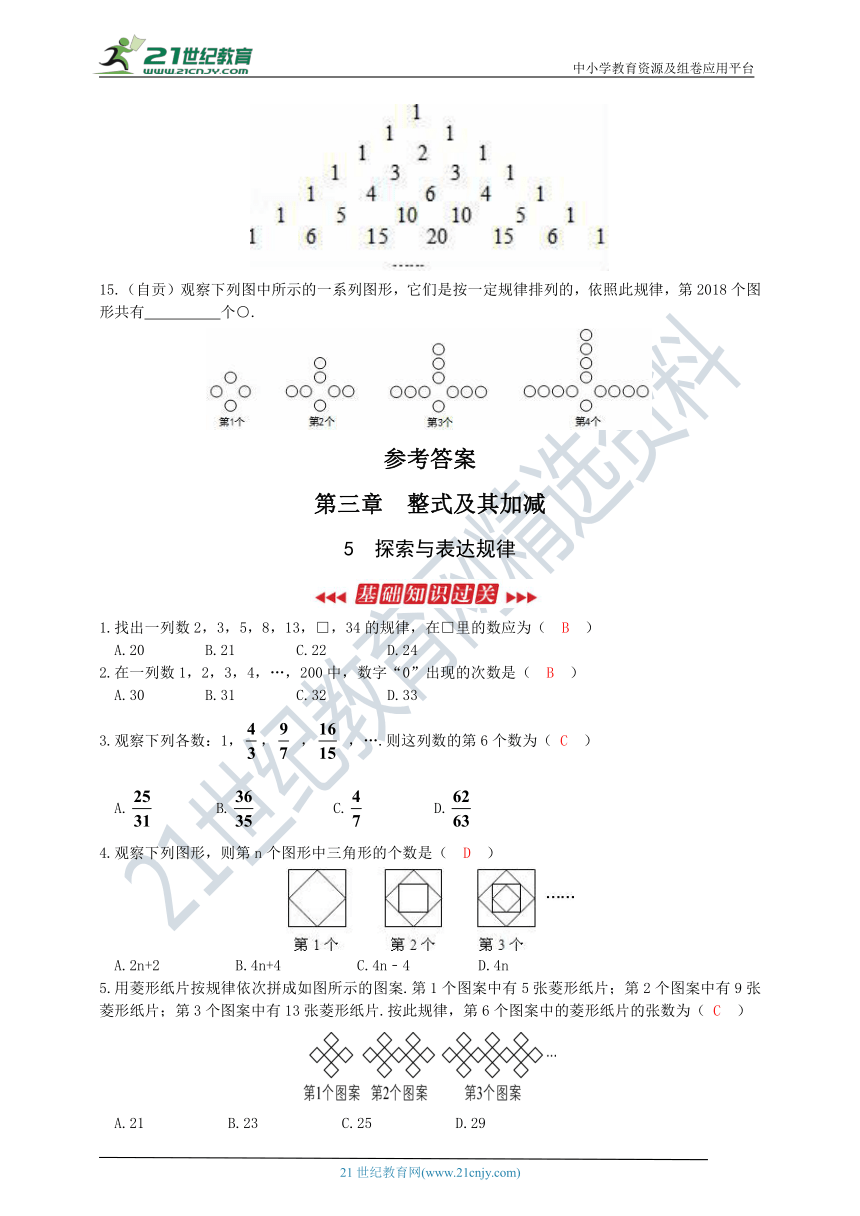
14.(孝感)我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”从图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10,…,那么a4+a11﹣2a10+10的值是 .
/
15.(自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 个○.
/
参考答案
第三章 整式及其加减
5 探索与表达规律
/
1.找出一列数2,3,5,8,13,□,34的规律,在□里的数应为( B )
A.20 B.21 C.22 D.24
2.在一列数1,2,3,4,…,200中,数字“0”出现的次数是( B )
A.30 B.31 C.32 D.33
3.观察下列各数:1,, , ,….则这列数的第6个数为( C )
A. B. C. D.
4.观察下列图形,则第n个图形中三角形的个数是( D )
/
A.2n+2 B.4n+4 C.4n﹣4 D.4n
5.用菱形纸片按规律依次拼成如图所示的图案.第1个图案中有5张菱形纸片;第2个图案中有9张菱形纸片;第3个图案中有13张菱形纸片.按此规律,第6个图案中的菱形纸片的张数为( C )
/
A.21 B.23 C.25 D.29
6./ , ……,若 / 符合前面式子的规律, 则a+b = __109 __.
7.观察如下图形,按照这种方式摆下去,第(n)个图形需用 3n 枚棋子.
/
8.如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想,然后填空:当黑色瓷砖为20块时,白色瓷砖为__16___块;白色瓷砖为(为正整数)块时,黑色瓷砖为__4+4n___块.
/
/
9.将从1开始的自然数,按如图所示的规律排列,在2,3,5,7,10,13,17,…,处分别拐第1,2,3,4,5,6,7,…,次弯,则第33次拐弯处的那个数是( A )
/
A.290 B.226 C.272 D.302
10.如图,在日历中,任意圈出一竖列上相邻的三个数,设中间的数为a,则这三个数之和为 3a .
/
11.从2开始,连续的偶数相加,和的情况如下表:
加数的个数(n)
和(s)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
….
….
n个从2开始的连续偶数相加时,它们的和S与n之间有什么样的关系?用公式表示出来,并由此计算下列各题:
(1)2+4+6+8+…+202; (2)126+128+130+…+300.
解:S=n(n+1).
(1)2+4+6+8+…+202=101×(101+1)=10 302.
(2)126+128+130+…+300=(2+4+6+8+…+300)-(2+4+6+8+…+124)= 150×(150+1)-62×(62+1)=18 744.
12.用如图形状的三角形砖,按一定的方式搭起一个金字塔:
/
(1)观察图形,并填空:当金字塔分别搭到3层、4层、5层时,所用三角形砖的块数分别为: 9 、 16 、 25 ,又推断,当金字塔搭了n层时共用去三角形砖 n2 块;
(2)试推断,当金字塔搭到第99层时,底层需要多少三角形砖块;反之,若底层用了99块三角形砖时,则金字塔能搭几层?
解:①当金字塔搭到共99层时,底层需要的三角形砖块数为:2×99﹣1=197(块);
②若底层用了99块三角形砖时,可设金字塔能搭n层,则2n﹣1=99,∴n=50(层).
答:当金字塔搭到共50层时,底层三角形砖块数刚好为99块.
/
13.将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
/
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
解:(1)从表格知道中间的数为a,上面的为a﹣12,下面的为a+12,左面的为a﹣2,右面的为a+2,a+(a﹣2)+(a+2)+(a﹣12)+(a+12)=5a.
(2)令5a=2020,a=404,所以可以,5个数分别是392、402、404、406、416.
(3)令5a=365,a=73,所以可以,5个数分别是61、71、73、75、85.
/
14.(孝感)我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”从图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10,…,那么a4+a11﹣2a10+10的值是 ﹣24 .
/
15.(自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 6055 个○.
/
/
5 探索与表达规律
/
1.找出一列数2,3,5,8,13,□,34的规律,在□里的数应为( )
A.20 B.21 C.22 D.24
2.在一列数1,2,3,4,…,200中,数字“0”出现的次数是( )
A.30 B.31 C.32 D.33
3.观察下列各数:1,, , ,….则这列数的第6个数为( )
A. B. C. D.
4.观察下列图形,则第n个图形中三角形的个数是( )
/
A.2n+2 B.4n+4 C.4n﹣4 D.4n
5.用菱形纸片按规律依次拼成如图所示的图案.第1个图案中有5张菱形纸片;第2个图案中有9张菱形纸片;第3个图案中有13张菱形纸片.按此规律,第6个图案中的菱形纸片的张数为( )
/
A.21 B.23 C.25 D.29
6./ , ……,若 / 符合前面式子的规律, 则a+b = __ __.
7.观察如下图形,按照这种方式摆下去,第(n)个图形需用 枚棋子.
/
8.如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想,然后填空:当黑色瓷砖为20块时,白色瓷砖为____块;白色瓷砖为(为正整数)块时,黑色瓷砖为_____块.
/
/
9.将从1开始的自然数,按如图所示的规律排列,在2,3,5,7,10,13,17,…,处分别拐第1,2,3,4,5,6,7,…,次弯,则第33次拐弯处的那个数是( )
/
A.290 B.226 C.272 D.302
10.如图,在日历中,任意圈出一竖列上相邻的三个数,设中间的数为a,则这三个数之和为 .
/
11.从2开始,连续的偶数相加,和的情况如下表:
加数的个数(n)
和(s)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
….
….
n个从2开始的连续偶数相加时,它们的和S与n之间有什么样的关系?用公式表示出来,并由此计算下列各题:
(1)2+4+6+8+…+202; (2)126+128+130+…+300.
12.用如图形状的三角形砖,按一定的方式搭起一个金字塔:
/
(1)观察图形,并填空:当金字塔分别搭到3层、4层、5层时,所用三角形砖的块数分别为: 、 、 ,又推断,当金字塔搭了n层时共用去三角形砖 块;
(2)试推断,当金字塔搭到第99层时,底层需要多少三角形砖块;反之,若底层用了99块三角形砖时,则金字塔能搭几层?
/
13.将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
/
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
/
14.(孝感)我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”从图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10,…,那么a4+a11﹣2a10+10的值是 .
/
15.(自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 个○.
/
参考答案
第三章 整式及其加减
5 探索与表达规律
/
1.找出一列数2,3,5,8,13,□,34的规律,在□里的数应为( B )
A.20 B.21 C.22 D.24
2.在一列数1,2,3,4,…,200中,数字“0”出现的次数是( B )
A.30 B.31 C.32 D.33
3.观察下列各数:1,, , ,….则这列数的第6个数为( C )
A. B. C. D.
4.观察下列图形,则第n个图形中三角形的个数是( D )
/
A.2n+2 B.4n+4 C.4n﹣4 D.4n
5.用菱形纸片按规律依次拼成如图所示的图案.第1个图案中有5张菱形纸片;第2个图案中有9张菱形纸片;第3个图案中有13张菱形纸片.按此规律,第6个图案中的菱形纸片的张数为( C )
/
A.21 B.23 C.25 D.29
6./ , ……,若 / 符合前面式子的规律, 则a+b = __109 __.
7.观察如下图形,按照这种方式摆下去,第(n)个图形需用 3n 枚棋子.
/
8.如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想,然后填空:当黑色瓷砖为20块时,白色瓷砖为__16___块;白色瓷砖为(为正整数)块时,黑色瓷砖为__4+4n___块.
/
/
9.将从1开始的自然数,按如图所示的规律排列,在2,3,5,7,10,13,17,…,处分别拐第1,2,3,4,5,6,7,…,次弯,则第33次拐弯处的那个数是( A )
/
A.290 B.226 C.272 D.302
10.如图,在日历中,任意圈出一竖列上相邻的三个数,设中间的数为a,则这三个数之和为 3a .
/
11.从2开始,连续的偶数相加,和的情况如下表:
加数的个数(n)
和(s)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
….
….
n个从2开始的连续偶数相加时,它们的和S与n之间有什么样的关系?用公式表示出来,并由此计算下列各题:
(1)2+4+6+8+…+202; (2)126+128+130+…+300.
解:S=n(n+1).
(1)2+4+6+8+…+202=101×(101+1)=10 302.
(2)126+128+130+…+300=(2+4+6+8+…+300)-(2+4+6+8+…+124)= 150×(150+1)-62×(62+1)=18 744.
12.用如图形状的三角形砖,按一定的方式搭起一个金字塔:
/
(1)观察图形,并填空:当金字塔分别搭到3层、4层、5层时,所用三角形砖的块数分别为: 9 、 16 、 25 ,又推断,当金字塔搭了n层时共用去三角形砖 n2 块;
(2)试推断,当金字塔搭到第99层时,底层需要多少三角形砖块;反之,若底层用了99块三角形砖时,则金字塔能搭几层?
解:①当金字塔搭到共99层时,底层需要的三角形砖块数为:2×99﹣1=197(块);
②若底层用了99块三角形砖时,可设金字塔能搭n层,则2n﹣1=99,∴n=50(层).
答:当金字塔搭到共50层时,底层三角形砖块数刚好为99块.
/
13.将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图).
/
(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2020吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
解:(1)从表格知道中间的数为a,上面的为a﹣12,下面的为a+12,左面的为a﹣2,右面的为a+2,a+(a﹣2)+(a+2)+(a﹣12)+(a+12)=5a.
(2)令5a=2020,a=404,所以可以,5个数分别是392、402、404、406、416.
(3)令5a=365,a=73,所以可以,5个数分别是61、71、73、75、85.
/
14.(孝感)我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”从图中取一列数:1,3,6,10,…,记a1=1,a2=3,a3=6,a4=10,…,那么a4+a11﹣2a10+10的值是 ﹣24 .
/
15.(自贡)观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 6055 个○.
/
/
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
