2.2等差数列(共43张PPT)
图片预览








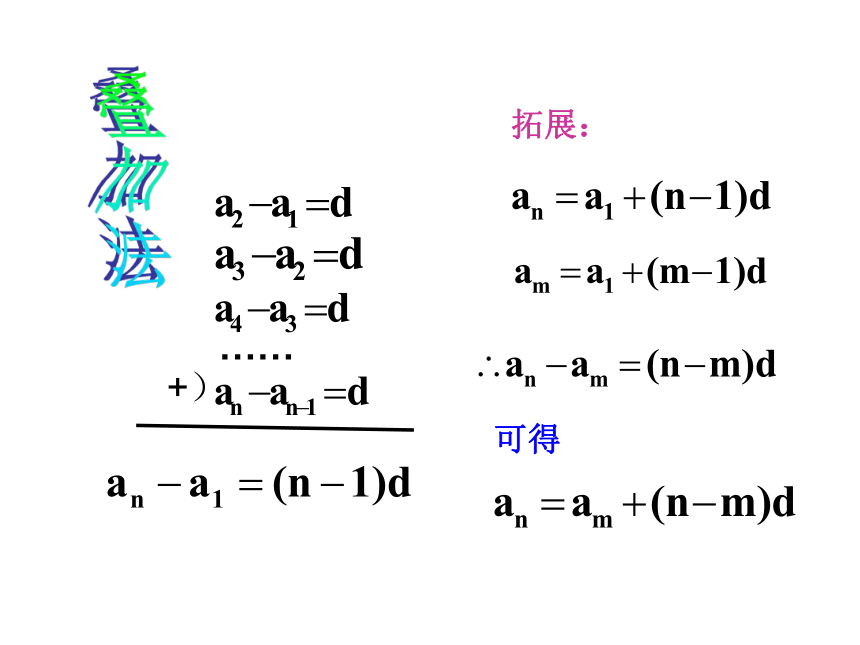
文档简介
(共43张PPT)
2.2 等差数列
1、数列的概念
2、导出数列的方法
你还记得吗?
首先对上一节课,进行回顾
回顾旧知
上两节课我们共同学习了数列的定义及给出数列的两种方法——通项公式和递推公式。这两个公式从不同的角度反映数列的特点,下面看这样一些例子
1,2,3,4,5,6;
10,8,6,4,2,0,-2;
2,2,2,2,2,2,2;
新课导入
1、某剧场前十排的座位数分别是:
48, 50, 52, 54, 56, 58,60, 62,64, 66 .
2、某运动员7天里的训练量是:
7550, 8050,8550, 9050, 9550, 10050,10550.
这些数列有什么特点,下面我们来学习。。。
好好学习
天天向上
1、 观察与思考 :下面的几个数列
从第2项起它们的后一项与前一项的差有什麽特点?
分析:后一项与前一项的差的特点是:
1,1,1,1,1,1 … 是常数1.
-3,-3,-3,-3,-3 … 是常数-3.
0.1,0.1, 0.1,0.1, 0.1 … 是常数0.1.
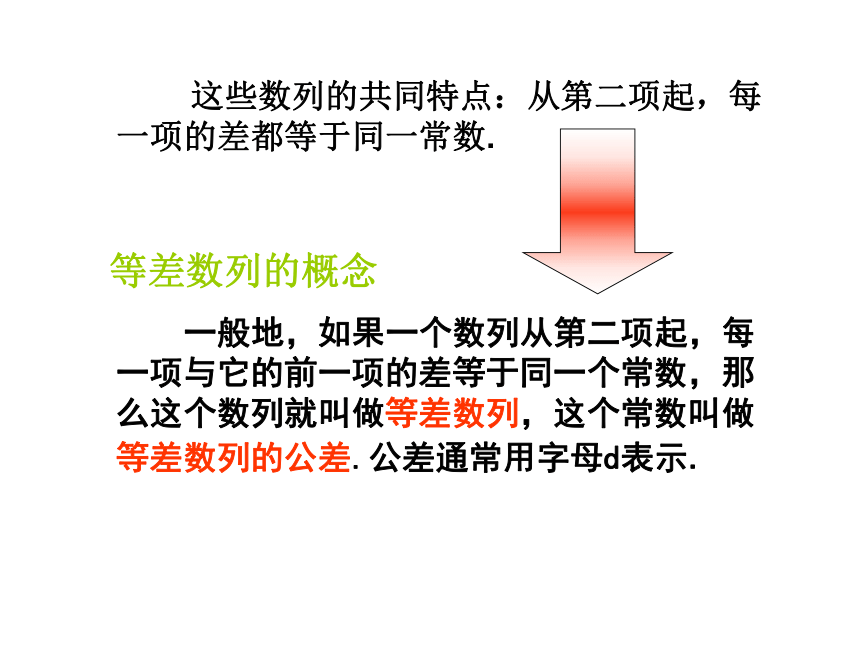
这些数列的共同特点:从第二项起,每一项的差都等于同一常数.
等差数列的概念
一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差.公差通常用字母d表示.
1.an-an-1=d (n≥2)(数学表达式)
等差数列公差的知识要点
2.公差是唯一的常数;
3.等差数列要求从第2项起,后一项与前一项作差.不能颠倒
4.作差的结果要求是同一个常数.
可以是整数,也可以是0和负数.
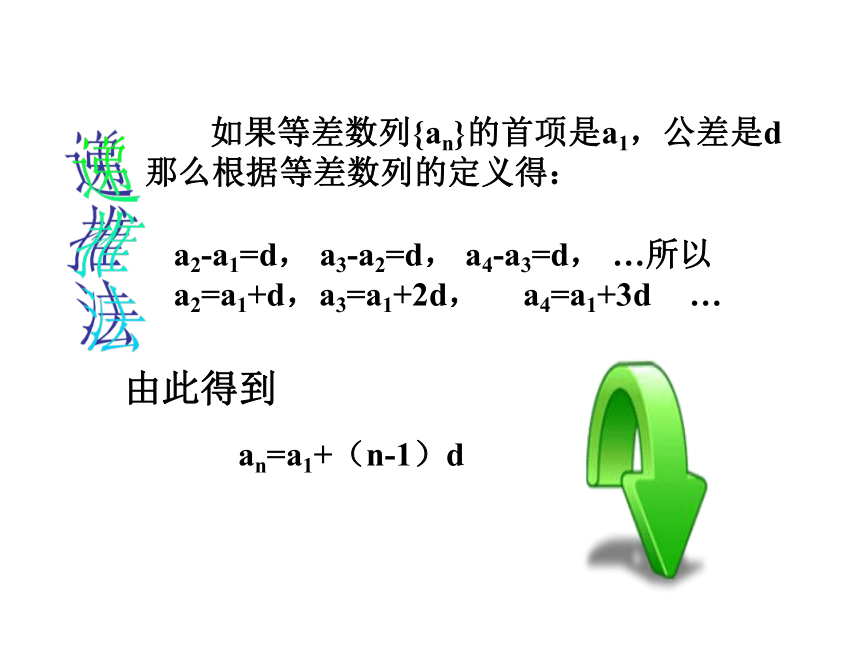
如果等差数列{an}的首项是a1,公差是d那么根据等差数列的定义得:
a2-a1=d, a3-a2=d, a4-a3=d, …所以a2=a1+d,a3=a1+2d, a4=a1+3d …
an=a1+(n-1)d
由此得到
【说明】 数列{ an }为等差数列?
an+1-an=d或an+1=an+d
当n=1时,上面等式两边均为a1,即等式也是成立的,这表明n∈N+时上面公式都成立,因而它就是等差数列的通项公式.
an=a1+(n-1)d
拓展:
由数列的单调性定义,易得
{an}为递增数列? d>0
{an}为递减数列? d<0
{an}为常数列? d=0
等差数列的单调性
(1)数列{an}是等差数列?an+1-an=d(常数).
(2)数列{an}是等差数列?an=a1+(n-1)d .
(3)数列{an}是等差数列?an=am+(n-m)d.
(4)数列{an}是等差数列?an=dn+b,其中d,b为常数.
(1)对于任意正整数n,都有an+1-an=a2-a1;
(2){an}的通项公式:an=(a2-a1)n+(2a1-a2);
(3)对于任意正整数m,n,q,p,若m+n=q+p,则am+an=ap+aq.
判断是否为等差数列
解析(1)、该数列的第2项与第一项的差是1,其余的后一 项与 前一项的差都是2.不符合等差数的定义 要求从第2项起后项与前项的差是同一个常数. 所以, 它不是等差数列.
(2)、不是. 理由同(1).
(3)、是. 它符合等差数列的定义.
注意:
1、等差数列要求从第2项起,后一项与
前一项作差. 不能颠倒.
2、作差的结果要求是同一个常数.
可以是整数,也可以是0和负数.
(4)、不是。因为他从第2项起后项与前项的差是 :1,2 , 3 ,4 ,5 ,‥‥是常数,但不是同一常数. 所以不是.
等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A应满足什么条件?
由a,A, b成等差数列,得
A-a=b-A
所以A=
如果a,A,b成等差数列,那么A叫做a与b的等差中项.
解析:由已知条件得通项公式为:a12=a1+(12-1)d,带入得d=7所以,梯子中间各级的宽度从上到下依次是40cm,47cm,54cm,61cm,68cm,75cm,82cm,89cm,96cm,103cm.
梯子的最高一级宽33cm,最低一级宽110cm,其中还有10级,各级的宽度成等差数列,计算中间各级的宽度.
(2)、求等差数列 10 ,8 , 6 ,4 ,‥‥的第20项.
(1)、已知等差数列的首项 a1是3,公差 d 是2,求它 的通项公式.
(3)、 -401是不是等差数列 –5 , -9 ,-13 ,‥‥的项 ?如果是,是第几项?
例 1:
(1)分析:知道a1 ,d,求an 。代入通项公式。
解:
∵ a1=3 , d=2
∴ an=a1+(n-1)d
=3+(n-1) ×2
=2n+1
解: ∵ a1=10, d=8-10= -2 , n=20
由an=a1+(n-1)d 得
∴ a20 =a1+(n-1)d
=10+(20-1)×(-2)
= -28
(2)分析:根据a1=10,d= -2,先求出通项公式an ,再求出a20
解: ∵ a1= -5, d= -9-(-5)= -4
∴ an= -5+(n-1) ×(-4)
= -4n-1
∵ -401= -4n-1
∴n=100
∴ -401是该数列的第100项.
(3)分析:根据a1= -5,d= -4,先求出通项公式an ,再把 –401代入,然后看是否存在正整数n .
若a1+a4+a7=39, a2+a5+a8=33,则a3+a6+a9= ——.
分析:这是一组求等差数列中某些元素的问题,考察等差数列的基本参数和其性质.
例2、
数列a1+a4+a7,a2+a5+a8,a3+a6+a9也是等差数列,所以:
2( a2+a5+a8 )=( a1+a4+a7 )+ ( a3+a6+a9 )
所以: a3+a6+a9=2×33-39=27
解:
在等差数列{an}中 ,已知a6=12 ,a18=36 ,求首项a1 ,公差 d 及通项an .
分析: 此题已知a6=12 ,n=6 ;a18=36 , n=18分别代入通项, 公式an = a1+(n-1)d 中 ,可得两个方程,都含a1与d两个未知 数组成方程组,可解出a1与d .
例3:
∴ an = 2+(n-1) ×2 = 2n
∴ d = 2 a1 =2
解:
由题意可得
a1+5d=12 ①
a1+17d=36 ②
1、 等差数列的概念.必须从第2项起后项减去前项,并且差是 同 一常数.
2、等差数列的通项公式 an = a1+(n-1)d 知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量.
课堂小结
3、等差数列{an}中an=a1+(n-1)
d,可整理为an=dn+(a1-d).
4、如果a,A,b成等差数列,那
么A叫做a与b的等差中项.
记一记
高考链接
1.(2019 湖南)设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则s7等于 ( )
A. 13 B.35 C.49 D.63
C
B
(1)、求等差数列 3 ,7 , 11 ,‥‥的第4项和第10项。
(2)、100是不是等差数列 2 ,9 , 16 ,‥‥的项?如果是,是第几项?如果不是,说明理由。
(3)、 -20是不是等差数列 0 ,-3.5 ,-7 ,‥‥的项?如果是, 是第几项?如果不是,说明理由。
1、做一做:
随堂练习
(1)∵ a1=3 ,
d=7-3= 4
∴ an=3+4(n-1)
= 4n-1
∴ a4=4×4-1=15 ,
a10=4×10 –1=39.
答案:
(2)∵ a1=2 ,d=9-2=7
∴ an=2+7(n-1)
= 7n-5
∵ 100=7n-5
∴ n =15
∴ 100是该数列的第15项.
(3)∵ a1=0 , d= -3.5 -0= -3.5
∴ an=0-3.5(n-1)
= -3.5n+3.5
∵ -20= -3.5n+3.5无正整数解
∴ -20不是该数列的项.
已知等差数列的通项公式,an , a1 , n ,d 这四个变量,知道其中三个量就可以求余下的一个量.
1.在等差数列{an}中,
(1)已知 a4=10 , a7=19 ,求 a1与 d .
(2)已知 a3=9 , a9=3 ,求 a12 .
本题主要考查等差数列的通项公式,属于最基本的题目.
小试牛刀
(1)由题意得
解:
(2)由题意得
在解题过程中灵活运用等差数列的性质是提高解题速度的关键。
高考pk,不让一招一式.
(05年福建)已知等差数列{an}中,a7+a9=16,a4=1, 则a12的值是( )
解析高考
利用公式
对于任意正整数m,n,q,p,若m+n=q+p,则am+an=ap+aq
带入得a12=15.
a7+a9=a4+a12
高考预测题
若a1-a4-a8-a12+a15=2,则a3+a13= ——.
高瞻远瞩,不弃一草一木.
法一:由条件式,可得a1-(a1+3d)-(a1+7d)-(a1+11d)+(a1+14d)=2得:a1+7d=-2
所以a3+a13=2a8=2(a1+7d)=-4
法二:2a8=a1+a15=a4+a12,
a8=-2所以a3+a13=2a8=-4
解析:
2.2 等差数列
1、数列的概念
2、导出数列的方法
你还记得吗?
首先对上一节课,进行回顾
回顾旧知
上两节课我们共同学习了数列的定义及给出数列的两种方法——通项公式和递推公式。这两个公式从不同的角度反映数列的特点,下面看这样一些例子
1,2,3,4,5,6;
10,8,6,4,2,0,-2;
2,2,2,2,2,2,2;
新课导入
1、某剧场前十排的座位数分别是:
48, 50, 52, 54, 56, 58,60, 62,64, 66 .
2、某运动员7天里的训练量是:
7550, 8050,8550, 9050, 9550, 10050,10550.
这些数列有什么特点,下面我们来学习。。。
好好学习
天天向上
1、 观察与思考 :下面的几个数列
从第2项起它们的后一项与前一项的差有什麽特点?
分析:后一项与前一项的差的特点是:
1,1,1,1,1,1 … 是常数1.
-3,-3,-3,-3,-3 … 是常数-3.
0.1,0.1, 0.1,0.1, 0.1 … 是常数0.1.
这些数列的共同特点:从第二项起,每一项的差都等于同一常数.
等差数列的概念
一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差.公差通常用字母d表示.
1.an-an-1=d (n≥2)(数学表达式)
等差数列公差的知识要点
2.公差是唯一的常数;
3.等差数列要求从第2项起,后一项与前一项作差.不能颠倒
4.作差的结果要求是同一个常数.
可以是整数,也可以是0和负数.
如果等差数列{an}的首项是a1,公差是d那么根据等差数列的定义得:
a2-a1=d, a3-a2=d, a4-a3=d, …所以a2=a1+d,a3=a1+2d, a4=a1+3d …
an=a1+(n-1)d
由此得到
【说明】 数列{ an }为等差数列?
an+1-an=d或an+1=an+d
当n=1时,上面等式两边均为a1,即等式也是成立的,这表明n∈N+时上面公式都成立,因而它就是等差数列的通项公式.
an=a1+(n-1)d
拓展:
由数列的单调性定义,易得
{an}为递增数列? d>0
{an}为递减数列? d<0
{an}为常数列? d=0
等差数列的单调性
(1)数列{an}是等差数列?an+1-an=d(常数).
(2)数列{an}是等差数列?an=a1+(n-1)d .
(3)数列{an}是等差数列?an=am+(n-m)d.
(4)数列{an}是等差数列?an=dn+b,其中d,b为常数.
(1)对于任意正整数n,都有an+1-an=a2-a1;
(2){an}的通项公式:an=(a2-a1)n+(2a1-a2);
(3)对于任意正整数m,n,q,p,若m+n=q+p,则am+an=ap+aq.
判断是否为等差数列
解析(1)、该数列的第2项与第一项的差是1,其余的后一 项与 前一项的差都是2.不符合等差数的定义 要求从第2项起后项与前项的差是同一个常数. 所以, 它不是等差数列.
(2)、不是. 理由同(1).
(3)、是. 它符合等差数列的定义.
注意:
1、等差数列要求从第2项起,后一项与
前一项作差. 不能颠倒.
2、作差的结果要求是同一个常数.
可以是整数,也可以是0和负数.
(4)、不是。因为他从第2项起后项与前项的差是 :1,2 , 3 ,4 ,5 ,‥‥是常数,但不是同一常数. 所以不是.
等差中项
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A应满足什么条件?
由a,A, b成等差数列,得
A-a=b-A
所以A=
如果a,A,b成等差数列,那么A叫做a与b的等差中项.
解析:由已知条件得通项公式为:a12=a1+(12-1)d,带入得d=7所以,梯子中间各级的宽度从上到下依次是40cm,47cm,54cm,61cm,68cm,75cm,82cm,89cm,96cm,103cm.
梯子的最高一级宽33cm,最低一级宽110cm,其中还有10级,各级的宽度成等差数列,计算中间各级的宽度.
(2)、求等差数列 10 ,8 , 6 ,4 ,‥‥的第20项.
(1)、已知等差数列的首项 a1是3,公差 d 是2,求它 的通项公式.
(3)、 -401是不是等差数列 –5 , -9 ,-13 ,‥‥的项 ?如果是,是第几项?
例 1:
(1)分析:知道a1 ,d,求an 。代入通项公式。
解:
∵ a1=3 , d=2
∴ an=a1+(n-1)d
=3+(n-1) ×2
=2n+1
解: ∵ a1=10, d=8-10= -2 , n=20
由an=a1+(n-1)d 得
∴ a20 =a1+(n-1)d
=10+(20-1)×(-2)
= -28
(2)分析:根据a1=10,d= -2,先求出通项公式an ,再求出a20
解: ∵ a1= -5, d= -9-(-5)= -4
∴ an= -5+(n-1) ×(-4)
= -4n-1
∵ -401= -4n-1
∴n=100
∴ -401是该数列的第100项.
(3)分析:根据a1= -5,d= -4,先求出通项公式an ,再把 –401代入,然后看是否存在正整数n .
若a1+a4+a7=39, a2+a5+a8=33,则a3+a6+a9= ——.
分析:这是一组求等差数列中某些元素的问题,考察等差数列的基本参数和其性质.
例2、
数列a1+a4+a7,a2+a5+a8,a3+a6+a9也是等差数列,所以:
2( a2+a5+a8 )=( a1+a4+a7 )+ ( a3+a6+a9 )
所以: a3+a6+a9=2×33-39=27
解:
在等差数列{an}中 ,已知a6=12 ,a18=36 ,求首项a1 ,公差 d 及通项an .
分析: 此题已知a6=12 ,n=6 ;a18=36 , n=18分别代入通项, 公式an = a1+(n-1)d 中 ,可得两个方程,都含a1与d两个未知 数组成方程组,可解出a1与d .
例3:
∴ an = 2+(n-1) ×2 = 2n
∴ d = 2 a1 =2
解:
由题意可得
a1+5d=12 ①
a1+17d=36 ②
1、 等差数列的概念.必须从第2项起后项减去前项,并且差是 同 一常数.
2、等差数列的通项公式 an = a1+(n-1)d 知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量.
课堂小结
3、等差数列{an}中an=a1+(n-1)
d,可整理为an=dn+(a1-d).
4、如果a,A,b成等差数列,那
么A叫做a与b的等差中项.
记一记
高考链接
1.(2019 湖南)设Sn是等差数列{an}的前n项和,已知a2=3,a6=11,则s7等于 ( )
A. 13 B.35 C.49 D.63
C
B
(1)、求等差数列 3 ,7 , 11 ,‥‥的第4项和第10项。
(2)、100是不是等差数列 2 ,9 , 16 ,‥‥的项?如果是,是第几项?如果不是,说明理由。
(3)、 -20是不是等差数列 0 ,-3.5 ,-7 ,‥‥的项?如果是, 是第几项?如果不是,说明理由。
1、做一做:
随堂练习
(1)∵ a1=3 ,
d=7-3= 4
∴ an=3+4(n-1)
= 4n-1
∴ a4=4×4-1=15 ,
a10=4×10 –1=39.
答案:
(2)∵ a1=2 ,d=9-2=7
∴ an=2+7(n-1)
= 7n-5
∵ 100=7n-5
∴ n =15
∴ 100是该数列的第15项.
(3)∵ a1=0 , d= -3.5 -0= -3.5
∴ an=0-3.5(n-1)
= -3.5n+3.5
∵ -20= -3.5n+3.5无正整数解
∴ -20不是该数列的项.
已知等差数列的通项公式,an , a1 , n ,d 这四个变量,知道其中三个量就可以求余下的一个量.
1.在等差数列{an}中,
(1)已知 a4=10 , a7=19 ,求 a1与 d .
(2)已知 a3=9 , a9=3 ,求 a12 .
本题主要考查等差数列的通项公式,属于最基本的题目.
小试牛刀
(1)由题意得
解:
(2)由题意得
在解题过程中灵活运用等差数列的性质是提高解题速度的关键。
高考pk,不让一招一式.
(05年福建)已知等差数列{an}中,a7+a9=16,a4=1, 则a12的值是( )
解析高考
利用公式
对于任意正整数m,n,q,p,若m+n=q+p,则am+an=ap+aq
带入得a12=15.
a7+a9=a4+a12
高考预测题
若a1-a4-a8-a12+a15=2,则a3+a13= ——.
高瞻远瞩,不弃一草一木.
法一:由条件式,可得a1-(a1+3d)-(a1+7d)-(a1+11d)+(a1+14d)=2得:a1+7d=-2
所以a3+a13=2a8=2(a1+7d)=-4
法二:2a8=a1+a15=a4+a12,
a8=-2所以a3+a13=2a8=-4
解析:
