必修5第3章不等式.章末复习(共27张PPT)
文档属性
| 名称 | 必修5第3章不等式.章末复习(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 977.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
学法指导
1、不等式的基本概念,(理解其概念,要学会从实际生活中抽象出不等式;并学会用作差法判断不等式的符号方向.
2、熟练掌握实数的运算性质,从而利用它推导出不等式所具有的性质;并能利用这些基本性质进行简单的不等式证明.
3、掌握一元二次不等式一般形式的内涵,掌握解一元二次不等式的基本步骤,即所谓的“三步曲”;
4、学会从 实际问题中抽象出一元二次不等式的模型,并能运用“三部曲”将其解决;
5、二元一次不等式(组)的解集就可以看成是直角坐标系内的点构成的集合,学会用画图的方法表示它;
6、线性规划问题是掌握解线性规划问题的步骤,画、移、求、答,学会用画图法解决最值问题;
7、掌握基本不等式的代数证法和几何意义,学会利用基本不等式进行实际问题的分析和解决;学会利用分析法证明不等式.
要点总结
不等关系与不等式
一元二次不等
式及其解法
二元不次不等
式(组)与平面
区域
简单的线性规划问题
基本不等式
最值问题
1、代数式的大小比较或证明通常用作差比较法;
2、比较大小或证明的一般过程为:
3、常用不等式:
作差,化积,判断,结论;
3.1 不等关系与不等式
1、一元二次不等式的定义
我们把只含有一个未知数,并且未知数的最高次数为2次的不等式称为一元二次不等式.
3.2 一元二次不等式及其解法
2、一元二次方程的一般形式
<0
3、解一元二次不等式的基本步骤:“三步曲”
(1)转化为不等式的“标准”形式;
(2)算△,解相应一元二次方程的根;
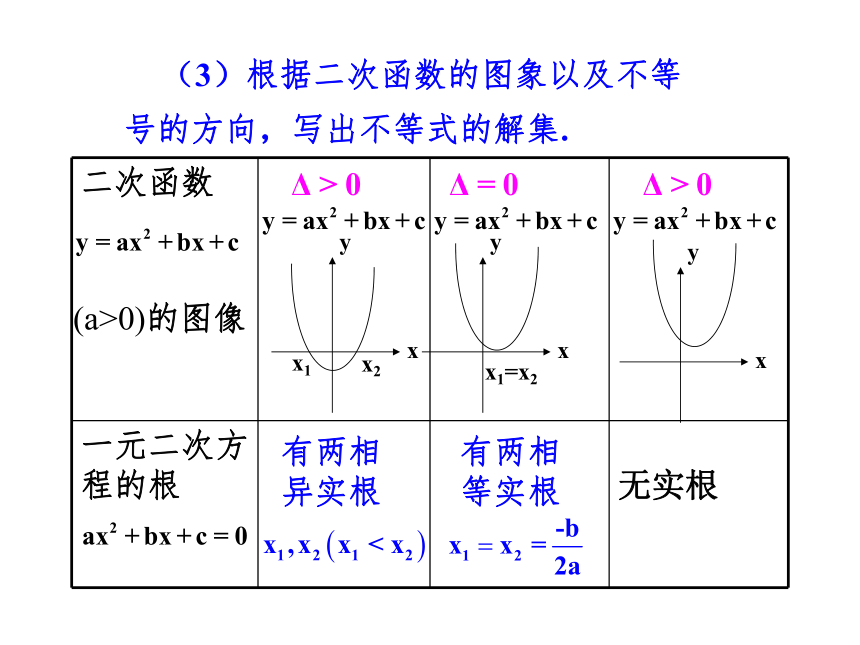
(3)根据二次函数的图象以及不等
号的方向,写出不等式的解集.
(a>0)的图像
有两相异实根
有两相等实根
二次函数
一元二次方 程的根 无实根
的解集
的解集
R
4、解一元二次不等式的步骤:
(1) 将二次项系数化为 正号;
(2)计算判别式,分析不等式的解的情况:
ⅰ. △ >0时,求根x1A>0,x>x1或xA<0,x1ⅱ.△=0时,求根x1=x2,
A>0,x≠x1
A<0, φ
A=0,x=x1
ⅲ. △ <0时,方程无解,
A>0,R
A≤0, φ
(3) 写出解集.
5、一元二次方程、一元二次不等式和二次函数的关系.
(1)二次方程的根是函数的零点,即二次函数图象与x轴交点的横坐标;
(2) 结合方程的解与函数图象可以得出二次不等式的解.
3.3二元一次不等式(组)与线性规划
3.31二元一次不等式(组)与平面区域
问题等式及其解法
2、二元一次不等式组:
有几个二元一次不等式组成的不等式组称为二元一次不等式组 ;
1、二元一次不等式:
含有两个未知数,并且未知数的最高次数是1的不等式叫做二元一次不等式 ;
3、二元一次不等式(组)的解集:
满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集 ;
4、一个一元二次方程表示的应为直线Ax+By+C=0某一侧所有的点组成的平面区域.
5、二元一次不等式表示哪个平面区域的判断方法:
由于对在直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点);
3.32简单的线性规划问题
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数 .
1、线性目标函数;
在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题 .
2、线性约束条件
3、线性规划问题:
4、可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域 .
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
6、解线性规划问题的步骤:
(1)画:画出线性约束条件所表示的可行域;
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案.
3.4基本不等式
1、如果把
看作是正数a、b的等差中项,
看作是正数a、b的等比中项,
那么我们有
以下结论为:两个正数的等差中项不小于它们的等比中项.
2、在数学中,我们称
为a、b的算术
平均数 ,称
为a、b的几何平均数.本节
结论还可叙述为:两个正数的算术平均数不小于它们的几何平均数.
3、两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M
为定值,则ab
等号当且仅当a=b时成立.
4、两个正数的积为定值时,它们的和有最小值,即若a,b∈R+,且ab=P,P为定值,则a+b
等号当且仅当a=b时
成立 .
5、利用重要不等式求函数的最值时务必注意三点达到:一正二定三能等!
(1)各项必须为正;
(2)含变数的各项和或积必须为定值;
(3)必须有自变量值能使函数取到 = 号.
6、应用基本不等式时,主要用到的方法和技巧是:凑、拆,使之出现和为定值或积为定值特征.
高考热点
1、不等式的性质
2、二元一次不等式表示哪个平面区域的判断方法:
由于对在直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点);
直线定界,特殊点定域
3、解线性规划问题的步骤:
(1)画:画出线性约束条件所表示的可行域;
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案.
4、用均值不等式解决问题时,应按如下步骤进行:
1、先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数;
2、建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
3、在定义域内,求出函数的最大值或最小值;
4、正确写出答案.
本章易错点
1、解二元与此不等式时忽视二次项系数a应该大于零;
2、在确定二元一次不等式表示哪个平面区域时,忽略当直线过原点时,应带的点为(0,1),而不是(0,0);
3、在应用基本不等式
忽视它等号成立的条件.
时,
学法指导
1、不等式的基本概念,(理解其概念,要学会从实际生活中抽象出不等式;并学会用作差法判断不等式的符号方向.
2、熟练掌握实数的运算性质,从而利用它推导出不等式所具有的性质;并能利用这些基本性质进行简单的不等式证明.
3、掌握一元二次不等式一般形式的内涵,掌握解一元二次不等式的基本步骤,即所谓的“三步曲”;
4、学会从 实际问题中抽象出一元二次不等式的模型,并能运用“三部曲”将其解决;
5、二元一次不等式(组)的解集就可以看成是直角坐标系内的点构成的集合,学会用画图的方法表示它;
6、线性规划问题是掌握解线性规划问题的步骤,画、移、求、答,学会用画图法解决最值问题;
7、掌握基本不等式的代数证法和几何意义,学会利用基本不等式进行实际问题的分析和解决;学会利用分析法证明不等式.
要点总结
不等关系与不等式
一元二次不等
式及其解法
二元不次不等
式(组)与平面
区域
简单的线性规划问题
基本不等式
最值问题
1、代数式的大小比较或证明通常用作差比较法;
2、比较大小或证明的一般过程为:
3、常用不等式:
作差,化积,判断,结论;
3.1 不等关系与不等式
1、一元二次不等式的定义
我们把只含有一个未知数,并且未知数的最高次数为2次的不等式称为一元二次不等式.
3.2 一元二次不等式及其解法
2、一元二次方程的一般形式
<0
3、解一元二次不等式的基本步骤:“三步曲”
(1)转化为不等式的“标准”形式;
(2)算△,解相应一元二次方程的根;
(3)根据二次函数的图象以及不等
号的方向,写出不等式的解集.
(a>0)的图像
有两相异实根
有两相等实根
二次函数
一元二次方 程的根 无实根
的解集
的解集
R
4、解一元二次不等式的步骤:
(1) 将二次项系数化为 正号;
(2)计算判别式,分析不等式的解的情况:
ⅰ. △ >0时,求根x1
A>0,x≠x1
A<0, φ
A=0,x=x1
ⅲ. △ <0时,方程无解,
A>0,R
A≤0, φ
(3) 写出解集.
5、一元二次方程、一元二次不等式和二次函数的关系.
(1)二次方程的根是函数的零点,即二次函数图象与x轴交点的横坐标;
(2) 结合方程的解与函数图象可以得出二次不等式的解.
3.3二元一次不等式(组)与线性规划
3.31二元一次不等式(组)与平面区域
问题等式及其解法
2、二元一次不等式组:
有几个二元一次不等式组成的不等式组称为二元一次不等式组 ;
1、二元一次不等式:
含有两个未知数,并且未知数的最高次数是1的不等式叫做二元一次不等式 ;
3、二元一次不等式(组)的解集:
满足二元一次不等式(组)的x和y的取值构成有序实数对(x,y),所有这样的有序实数对(x,y)构成的集合称为二元一次不等式(组)的解集 ;
4、一个一元二次方程表示的应为直线Ax+By+C=0某一侧所有的点组成的平面区域.
5、二元一次不等式表示哪个平面区域的判断方法:
由于对在直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点);
3.32简单的线性规划问题
关于x、y的一次式z=2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数 .
1、线性目标函数;
在上述问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.
一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题 .
2、线性约束条件
3、线性规划问题:
4、可行解、可行域和最优解:
满足线性约束条件的解(x,y)叫可行解.
由所有可行解组成的集合叫做可行域 .
使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.
6、解线性规划问题的步骤:
(1)画:画出线性约束条件所表示的可行域;
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案.
3.4基本不等式
1、如果把
看作是正数a、b的等差中项,
看作是正数a、b的等比中项,
那么我们有
以下结论为:两个正数的等差中项不小于它们的等比中项.
2、在数学中,我们称
为a、b的算术
平均数 ,称
为a、b的几何平均数.本节
结论还可叙述为:两个正数的算术平均数不小于它们的几何平均数.
3、两个正数的和为定值时,它们的积有最大值,即若a,b∈R+,且a+b=M,M
为定值,则ab
等号当且仅当a=b时成立.
4、两个正数的积为定值时,它们的和有最小值,即若a,b∈R+,且ab=P,P为定值,则a+b
等号当且仅当a=b时
成立 .
5、利用重要不等式求函数的最值时务必注意三点达到:一正二定三能等!
(1)各项必须为正;
(2)含变数的各项和或积必须为定值;
(3)必须有自变量值能使函数取到 = 号.
6、应用基本不等式时,主要用到的方法和技巧是:凑、拆,使之出现和为定值或积为定值特征.
高考热点
1、不等式的性质
2、二元一次不等式表示哪个平面区域的判断方法:
由于对在直线Ax+By+C=0同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同,所以只需在此直线的某一侧取一特殊点(x0,y0),从Ax0+By0+C的正负即可判断Ax+By+C>0表示直线哪一侧的平面区域.(特殊地,当C≠0时,常把原点作为此特殊点);
直线定界,特殊点定域
3、解线性规划问题的步骤:
(1)画:画出线性约束条件所表示的可行域;
(2)移:在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案.
4、用均值不等式解决问题时,应按如下步骤进行:
1、先理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数;
2、建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
3、在定义域内,求出函数的最大值或最小值;
4、正确写出答案.
本章易错点
1、解二元与此不等式时忽视二次项系数a应该大于零;
2、在确定二元一次不等式表示哪个平面区域时,忽略当直线过原点时,应带的点为(0,1),而不是(0,0);
3、在应用基本不等式
忽视它等号成立的条件.
时,
