必修5第二章数列 章末复习(共22张PPT)
文档属性
| 名称 | 必修5第二章数列 章末复习(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第二章 数列
学法指导
(1)为激发学生学习数列的兴趣,体会数列知识在实际生活中的作用,可由实际问题引入,从中抽象出数列要研究的问题,使学生对所要研究的内容心中有数,如书中所给的例子,还有物品堆放个数的计算等.
(2)由数列的通项公式写出数列的前几项是简单的代入法,教师精心设计例题,使这一例题为写通项公式作一些准备,尤其是对程度差的学生,应多举几个例子,让学生观察归纳通项公式与各项的结构关系,尽量为写通项公式提供帮助.
(3)数列中蕴含的函数思想是研究数列的指导思想,应及早引导学生发现数列与函数的关系.在教学中强调数列的项是按一定顺序排列的.由于数列的自变量为正整数,于是就有可能相邻的两项(或几项)有关系,从而数列就有其特殊的表示法——递推公式法.
(4)由数列的前几项写出数列的一个通项公式使学生学习中的一个难点,要帮助学生分析各项中的结构特征(整式,分式,递增,递减,摆动等),由学生归纳一些规律性的结论,如正负相间用 来调整等.如果学生一时不能写出通项公式,可让学生依据前几项的规律,猜想该数列的下一项或下几项的值,以便寻求项与项数的关系.
(5)对每个数列都有求和问题,所以在本节课应补充数列前 项和的概念,用 表示 的问题是重点问题,可先提出一个具体问题让学生分析 与 的关系,再由特殊到一般,研究其一般规律,并给出严格的推理证明(强调 的表达式是分段的);之后再到特殊问题的解决,举例时要兼顾结果可合并及不可合并的情况.
其实关键还是"理解"...多做题,多总结规律!...
(6)给出一些简单数列的通项公式,可以求其最大项或最小项,又是函数思想与方法的体现,对程度好的学生应提出这一问题,学生运用函数知识是可以解决的.
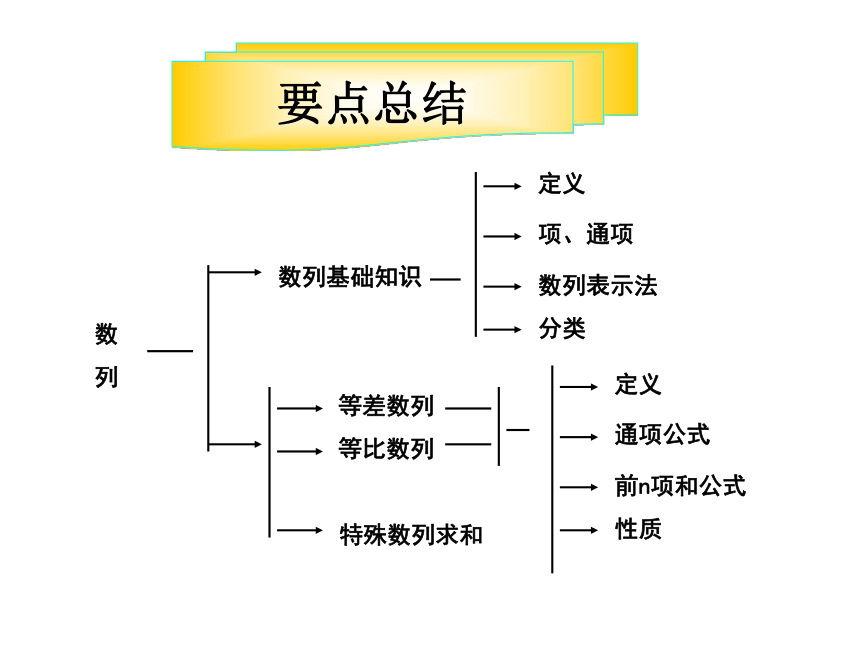
要点总结
一.数列的有关概念
②数列也可以看作是一个定义域为自然数集N或N的有限子集{1,2,…n}的函数当自变量从小到大依次取值时对应的一列函数值,通项公式就是这一函数的解析式.
③两种基本数列——等差数列、等比数列,是高考中的必考内容,要熟练掌握这两种数列的定义、通项公式、前 n 项和公式以及其性质.
①数列是按一定次序排列的一列数.
二.等差数列和等比数列
1.通项公式
等差数列 等比数列
2.前 n 项和
n 的系数k就是公差
特 征
特 征
是关于n 的不含常数项的二次函数
a 的n 次幂的系数与常数项互为相反 数。
底数a就是公比
3.性质 等差数列 等比数列
三.如何求数列的通项
1.归纳法:
对于数列中所给出的一些项,逐项分析项与项数n的关系,由此归纳出一般的公式.
在使用这种方法时要经常用到一些基本数列的通项公式,例如:自然数列、奇偶数列、自然数平方数列、倒数数列、幂数列、符号数列等.
2.利用前n项和与通项的关系求通项公式
3.利用递推关系,构造新数列。
(叠加)
(叠乘)
四.如何求数列的和
1.裂项求和
3.错位相减
2.分组求和
数列求和,一是把一个未知的数列变成若干个已知的数列,利用公式求和;二是把数列整理化简,使某些项相约、相消,成为关于n的一个代数式。归纳起来,常用的方法有如下几种.
4.倒序相加
1.裂项求和
把通项公式分成若干个已知数列的和,分别用公
式求这些数列的和,从而求出原数列的和.
2. 分组求和
与裂项求和相反,有时需要把数列的若干项分成一组,
求出每个组中的数列之和,作为新数列的项,再求和.
3.错位相减求和
若一个数列的通项等于一个等差数列与一个等比数列的积,可考虑用此法求和.
4.倒序相加求和
仿推导等差数列和的方法,把某些数列首尾
对称的项对应相加,有时也可得到不错的效果.
高考热点
1、数列的有关概念.
2、等差数列和等比数列的通项公式,前n项和特征及性质.
3、求数列通项公式的方法:归纳法、利用前n项和与通项的关系求通项公式、利用递推关系,构造新数列.
4、数列求和的方法:裂项求和、分组求和、倒序相加、错位相减.
本章易错点
1、在等比数列中,对于公比q有三个极易出错的点:0,1,-1。这“三个点”与公比可谓是“形影相随”,稍有不慎,就会产生错误.
2、忘了考虑求数列的通项公式及求数列和的时候当n=1的情况.
第二章 数列
学法指导
(1)为激发学生学习数列的兴趣,体会数列知识在实际生活中的作用,可由实际问题引入,从中抽象出数列要研究的问题,使学生对所要研究的内容心中有数,如书中所给的例子,还有物品堆放个数的计算等.
(2)由数列的通项公式写出数列的前几项是简单的代入法,教师精心设计例题,使这一例题为写通项公式作一些准备,尤其是对程度差的学生,应多举几个例子,让学生观察归纳通项公式与各项的结构关系,尽量为写通项公式提供帮助.
(3)数列中蕴含的函数思想是研究数列的指导思想,应及早引导学生发现数列与函数的关系.在教学中强调数列的项是按一定顺序排列的.由于数列的自变量为正整数,于是就有可能相邻的两项(或几项)有关系,从而数列就有其特殊的表示法——递推公式法.
(4)由数列的前几项写出数列的一个通项公式使学生学习中的一个难点,要帮助学生分析各项中的结构特征(整式,分式,递增,递减,摆动等),由学生归纳一些规律性的结论,如正负相间用 来调整等.如果学生一时不能写出通项公式,可让学生依据前几项的规律,猜想该数列的下一项或下几项的值,以便寻求项与项数的关系.
(5)对每个数列都有求和问题,所以在本节课应补充数列前 项和的概念,用 表示 的问题是重点问题,可先提出一个具体问题让学生分析 与 的关系,再由特殊到一般,研究其一般规律,并给出严格的推理证明(强调 的表达式是分段的);之后再到特殊问题的解决,举例时要兼顾结果可合并及不可合并的情况.
其实关键还是"理解"...多做题,多总结规律!...
(6)给出一些简单数列的通项公式,可以求其最大项或最小项,又是函数思想与方法的体现,对程度好的学生应提出这一问题,学生运用函数知识是可以解决的.
要点总结
一.数列的有关概念
②数列也可以看作是一个定义域为自然数集N或N的有限子集{1,2,…n}的函数当自变量从小到大依次取值时对应的一列函数值,通项公式就是这一函数的解析式.
③两种基本数列——等差数列、等比数列,是高考中的必考内容,要熟练掌握这两种数列的定义、通项公式、前 n 项和公式以及其性质.
①数列是按一定次序排列的一列数.
二.等差数列和等比数列
1.通项公式
等差数列 等比数列
2.前 n 项和
n 的系数k就是公差
特 征
特 征
是关于n 的不含常数项的二次函数
a 的n 次幂的系数与常数项互为相反 数。
底数a就是公比
3.性质 等差数列 等比数列
三.如何求数列的通项
1.归纳法:
对于数列中所给出的一些项,逐项分析项与项数n的关系,由此归纳出一般的公式.
在使用这种方法时要经常用到一些基本数列的通项公式,例如:自然数列、奇偶数列、自然数平方数列、倒数数列、幂数列、符号数列等.
2.利用前n项和与通项的关系求通项公式
3.利用递推关系,构造新数列。
(叠加)
(叠乘)
四.如何求数列的和
1.裂项求和
3.错位相减
2.分组求和
数列求和,一是把一个未知的数列变成若干个已知的数列,利用公式求和;二是把数列整理化简,使某些项相约、相消,成为关于n的一个代数式。归纳起来,常用的方法有如下几种.
4.倒序相加
1.裂项求和
把通项公式分成若干个已知数列的和,分别用公
式求这些数列的和,从而求出原数列的和.
2. 分组求和
与裂项求和相反,有时需要把数列的若干项分成一组,
求出每个组中的数列之和,作为新数列的项,再求和.
3.错位相减求和
若一个数列的通项等于一个等差数列与一个等比数列的积,可考虑用此法求和.
4.倒序相加求和
仿推导等差数列和的方法,把某些数列首尾
对称的项对应相加,有时也可得到不错的效果.
高考热点
1、数列的有关概念.
2、等差数列和等比数列的通项公式,前n项和特征及性质.
3、求数列通项公式的方法:归纳法、利用前n项和与通项的关系求通项公式、利用递推关系,构造新数列.
4、数列求和的方法:裂项求和、分组求和、倒序相加、错位相减.
本章易错点
1、在等比数列中,对于公比q有三个极易出错的点:0,1,-1。这“三个点”与公比可谓是“形影相随”,稍有不慎,就会产生错误.
2、忘了考虑求数列的通项公式及求数列和的时候当n=1的情况.
