苏科版九年级数学下册5.5二次函数解决问题同步练习解析版
文档属性
| 名称 | 苏科版九年级数学下册5.5二次函数解决问题同步练习解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-09 00:00:00 | ||
图片预览




文档简介
5.5二次函数解决问题
一、选择题(本大题共10小题,共30.0分)
1.国家决定对某药品价格分两次降价,若设平均每次降价的百分率为x,该药品原价为18元,降价后的价格为y元,则y关于x的函数表达式为( )
A. B. C. D.
2.国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )
A. B. C. D.
3.在半径为的圆面上,从中挖去一个半径为的圆面,剩下一个圆环的面积为,则y与x的函数关系式为( )
A. B.
C. D.
4.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系下列叙述正确的是( )
?
A. 小球的飞行高度不能达到15m B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s D. 小球飞出1s时的飞行高度为10m
5.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A. B.
C. D.
6.方程的根可视为函数的图象与函数的图象交点的横坐标,则方程的实根所在的范围是( )
A. B. C. D.
7.用60m长的篱笆围成矩形场地,矩形的面积S随着矩形的一边长L的变化而变化,要使矩形的面积最大,L的长度应为( )
A. B. 15m C. 20m D.
8.某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价为偶数提高( )
A. 8元或10元 B. 12元 C. 8元 D. 10元
9.已知抛物线和一点,过P点的直线l,若直线l与该抛物线只有一个交点,则这样的直线l的条数是( )
A. 0 B. 1 C. 2 D. 3
10.如图是抛物线形拱桥的剖面图,拱底宽12m,拱高8m, 设计警戒水位为6m,当拱桥内水位达到警戒水位时,拱桥内的水面宽度是( )
A. 3m B. 6m C. D.
二、填空题(本大题共10小题,共30.0分)
11.把一根长30cm的铁丝分为两部分,每一部分均弯曲成一个正三角形,它们的面积和的最小值是______.
12.用8米长的绳子围成的最大矩形面积为______.
13.某种商品每件进价为20元,调查表明:在某段时间内,若以每件x元,且x为整数出售可卖出件,若使利润最大,则每件商品的售价应为________元.
14.一根蜡烛长18cm,点燃后每小时燃烧6cm,燃烧剩下的长度与燃烧的时间小时之间的函数解析式是______,自变量x的取值范围______.
15.抛物线的最低点坐标是______.
16.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元.当一个旅行团的人数是______人时,这个旅行社可以获得最大的营业额.
17.已知抛物线过和两点,交y轴于C点,且,则该抛物线的解析式为___________________________.
18.如图,池中心竖直水管的顶端安一个喷水头,使喷出的 抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为____.
19.公路上行驶的汽车急刹车时的行驶路程与时间的函数表达式为,当遇到紧急情况时,司机急刹车,但由于惯性,汽车要滑行__________m才能停下来.
20.已知直线与y轴交于点A,与直线交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线的顶点在直线上移动若抛物线与菱形的边AB,BC都有公共点,则h的取值范围是? ? ? ? ??.
三、解答题(本大题共4小题,共40.0分)
21.我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.设每件童装降价x元时,平均每天可盈利y元.
(1)写出y与x的函数关系式;
(2)当该专卖店每件童装降价多少元时,平均每天盈利400元?
(3)该专卖店要想平均每天盈利600元,可能吗?请说明理由.
22.如图,是一块锐角三角形余料,边厘米,高厘米,要把它加工成矩形零件PQMN,使矩形的一边在BC上,其余两个顶点分别在AB、AC上
(1)当时,PN的长度是多少?
(2)设PN的长度是x厘米,PQ的长度是y厘米时,求y与x之间的函数关系式.
(3)当PN的长度是多少时,矩形零件PQMN的面积最大?
23.如图,抛物线与y轴交于点,对称轴为直线,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将面积分成2:3两部分,请直接写出P点坐标.
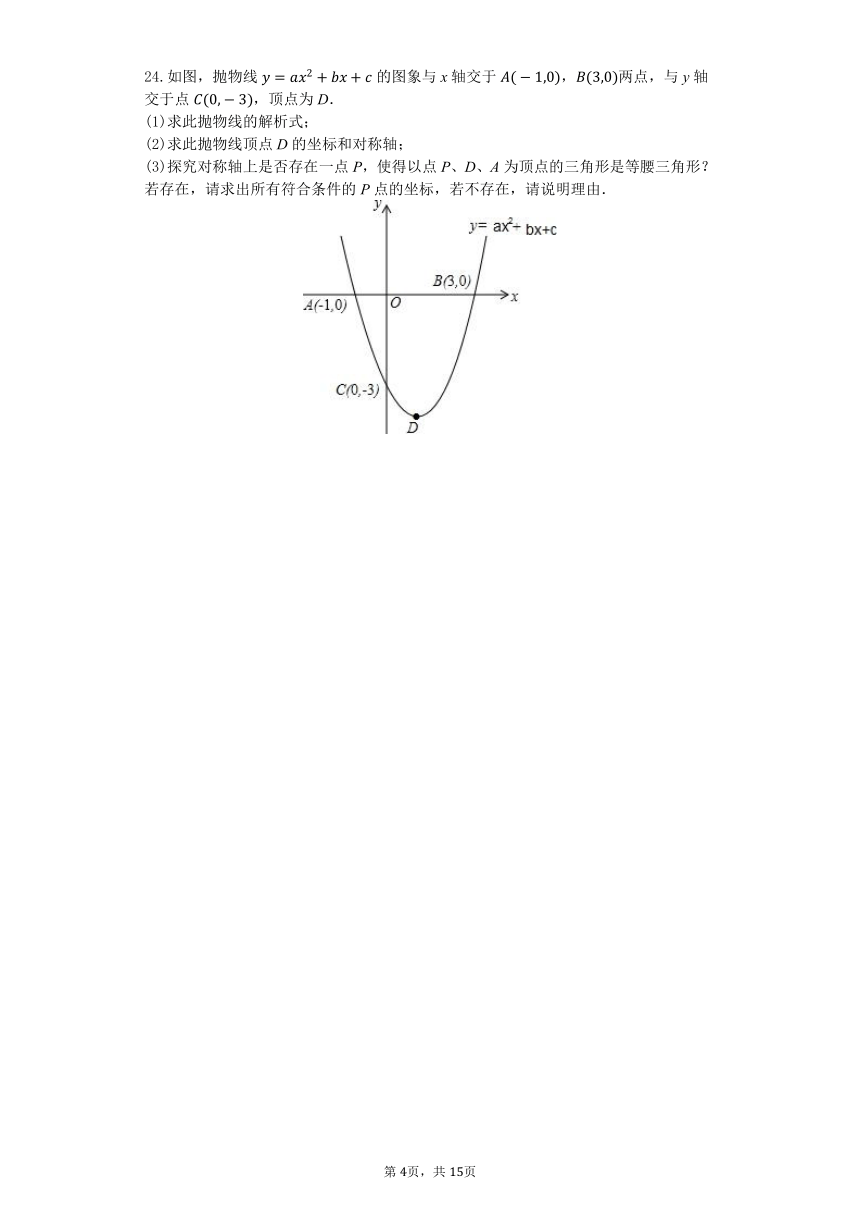
24.如图,抛物线的图象与x轴交于,两点,与y轴交于点,顶点为D.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和对称轴;
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
答案和解析
1.【答案】C
【解析】【分析】
此题主要考查了根据实际问题列二次函数解析式,本题需注意第二次降价是在第一次降价后的价格的基础上降价的原价为18,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则函数解析式即可求得.
【解答】
解:设平均每次降价的百分率为x,
根据题意可得:
y与x之间的函数关系为:.
故选C.
2.【答案】D
【解析】【分析】
此题主要考查了根据实际问题列二次函数解析式,本题需注意第二次降价是在第一次降价后的价格的基础上降价的.原价为33,第一次降价后的价格是,第二次降价是在第一次降价后的价格的基础上降价的为:,则函数解析式即可求得.
【解答】
解:设平均每次降价的百分比为x,根据题意可得:
y与x之间的函数关系为:.
故选D.
3.【答案】D
【解析】【分析】
本题考查了二次函数的应用,剩下面积半径为5的圆的面积半径为x的圆的面积根据题意,找到所求量的等量关系是解决问题的关键.
【解答】
解:半径为5的圆的面积,
半径为x的圆的面积,
函数解析式是:,
故选D.
4.【答案】C
【解析】【分析】
此题主要考查了二次函数的应用,正确解方程是解题关键.直接利用以及结合配方法求出二次函数最值分别分析得出答案.
【解答】
解:A、当时,,
解得:,,
故小球的飞行高度能达到15m,故此选项错误;
B、,
故时,小球的飞行高度最大为20m,故此选项错误;
C、时,,
解得:,,
小球从飞出到落地要用时4s,故此选项正确;
D、当时,,
故小球飞出1s时的飞行高度为15m,故此选项错误;
故选:C.
5.【答案】C
【解析】解:设销售单价为每千克x元,月销售利润为y元,
则y与x的函数关系式为:.
故选:C.
直接利用每千克利润销量总利润,进而得出关系式.
此题主要考查了根据实际问题抽象出二次函数关系式,正确表示出销量是解题关键.
6.【答案】C
【解析】解:方程,
,
它的根可视为和的图象交点的横坐标,
当时,,,此时抛物线的图象在反比例函数下方;
当时,,,此时抛物线的图象在反比例函数下方;
当时,,,此时抛物线的图象在反比例函数上方;
当时,,,此时抛物线的图象在反比例函数上方.
故方程的实根x所在范围为:.
故选:C.
首先根据题意推断方程的实根是函数与的图象交点的横坐标,再根据四个选项中x的取值代入两函数解析式,找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程的实根x所在范围.
此题考查了学生从图象中读取信息的数形结合能力.解决此类识图题,同学们要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.
7.【答案】B
【解析】【分析】
本题是二次函数的应用,属于图形面积问题,是常考题型,难度不大;熟练掌握各种几何图形的面积公式是关键,对于二次函数的最值,可以利用配方法求,也可以利用顶点坐标公式代入求解.根据矩形的面积长宽列式,配方求最值.
【解答】
解:由题意得:,
,
所以当时,S有最大值;
故选B.
8.【答案】A
【解析】【分析】
本题考查了二次函数的应用.此题为数学建模题,借助二次函数解决实际问题.
每件利润为元,销售量为,根据利润每件利润销售量,得出销售利润元与售单价元之间的函数关系;再根据函数关系式,利用二次函数的性质求最大利润.
【解答】
解:依题意,得
,,
抛物线开口向下,函数有最大值,
即当时,y的最大值为605,
售价为偶数,
为18或20,
当时,,
当时,,
为18或20时y的值相同,
商品提高了元或元,
故选A.
9.【答案】D
【解析】【分析】
本题考查了二次函数性质,正确的设出解析式并用一个系数表示出另一个系数是解答本题的关键.
由直线l与抛物线只有一个公共点,设直线l的解析式为,代入点P,得k、b的关系式,两者联立方程求得函数解析式即可得出有2条.当直线与抛物线的对称轴平行时也有一条,综合可得答案.
【解答】
解:分两种情况来讨论:
当直线与抛物线的对称轴不平行时,可设经过点的直线解析式为,
,
,
直线解析式为,
与抛物线只有一个交点
只有一个实数根,即方程的,
,
解得
过P点的不与对称轴平行的直线l,与抛物线只有一个交点的条数是2条.
当直线与抛物线的对称轴平行时,过点的直线于抛物线也只有一个公共点.
综合可得满足题意的直线有3条.
故选:D.
10.【答案】B
【解析】【分析】
本题考查二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题根据题意建立直角坐标系,如图,设抛物线的解析式为,由待定系数法求出其解即可.
【解答】
解:如图建立直角坐标系,
设抛物线的解析式为,
由题意,得
解得
?;
当时,即,
解得:,
拱桥内的水面宽度,
故选B.
11.【答案】
【解析】解:设第一个等边三角形的边长为xcm,则第二个等边三角形的边长为,设两个三角形的面积和为y,
根据题意得:.
,
当时,y取最小值,最小值为.
故答案为:.
设第一个等边三角形的边长为xcm,则第二个等边三角形的边长为,设两个三角形的面积和为y,根据等边三角形的性质结合三角形的面积公式即可得出y关于x的二次函数关系式,利用配方法结合二次函数的性质即可解决最值问题.
本题考查了二次函数的应用以及等边三角形的性质,解题的关键是得出y关于x的二次函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据三角形的面积找出y关于x的函数关系式是关键.
12.【答案】4
【解析】解:矩形的一边长为x米,面积为S平方米,
,
时,S取得最大值,此时,
故答案为:4
根据题意可以得到面积与边长的关系式,然后化为顶点式,即可解答本题.
本题考查二次函数的应用,能够列出二次函数关系式是解答此题的关键..
13.【答案】25
【解析】【分析】
本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.此题为数学建模题,借助二次函数解决实际问题.
本题是营销问题,基本等量关系:利润每件利润销售量,每件利润每件售价每件进价.再根据所列二次函数求最大值.
【解答】
解:设利润为w元,
则,
,
当时,二次函数有最大值25,
故答案是25.
14.【答案】,
【解析】解:根据题意,点燃后每小时耗去6cm,则x小时后,耗去6xcm,而蜡烛原长为18cm,
故有y与x之间的函数关系式是,
又由于,可得,
故答案为:,.
根据题意,点燃后每小时耗去6cm,则x小时后,耗去6xcm,而蜡烛原长为18cm,易得y与t之间的函数关系式;又根据实际意义,可得,计算可得x的范围.
此题考查了由实际问题列一次函数关系式的知识,读懂题意,找到相应的等量关系是解决本题的关键,注意求自变量的取值范围要考虑实际意义.
15.【答案】
【解析】解:
顶点,即最低点坐标是,
故答案为:.
利用配方法把抛物线的一般式转化为顶点式,再写出顶点坐标即可.
此题考查利用顶点式求函数的顶点坐标,注意根据函数解析式的特点灵活运用适当的方法解决问题.
16.【答案】55
【解析】解:设一个旅行团的人数是x人,设营业额为y元,根据题意可得:
,
故当一个旅行团的人数是55人时,这个旅行社可以获得最大的营业额.
故答案为:55.
直接根据题意表示出营业额,进而利用配方法求出答案.
此题主要考查了二次函数的应用,正确得出函数关系式是解题关键.
17.【答案】或
【解析】【分析】
本题考查二次函数的综合运用.涉及二次函数的图象与性质,待定系数法求二次函数解析式,三角形的面积.设二次函数解析式为,令,则,利用三角形面积公式有,求解即可.
【解答】
解:设二次函数解析式为,
令,则,
,
,
解得:,
,
即或.
故答案为或.
18.【答案】
【解析】解:由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:
,
代入求得:.
将a值代入得到抛物线的解析式为:
,
令,则.
则水管长为.
故答案为:.
设抛物线的解析式为,将代入求得a值,则时得的y值即为水管的长.
本题考查了二次函数在实际生活中的运用,重点是二次函数解析式的求法,利用顶点式求出解析式是解题关键.
19.【答案】20
【解析】【分析】
本题考查二次函数的实际应用,难度中等.由题意得,此题实际是求从开始刹车到停止所走的路程,即s的最大值.把抛物线的解析式化成顶点式后,即可解答.
【解答】
解:依题意该函数表达式可化为,
当时,汽车停下来,滑行了20m.
故由于惯性,汽车要滑行20m才能停下来.
故答案为20.
20.【答案】
【解析】【分析】本题主要考查的是二次函数的应用,解答本题主要应用了函数与方程的关系,求得抛物线与菱形的边AB、BC恰好都有公共点时h的值是解题的关键.
把代入 求得对应的y的值,从而可得到点A的坐标,然后将 与x联立求得方程组的解,从而可得到点B的坐标,接下来,依据抛物线的顶点在直线x上可得到h与k的关系,则抛物线的解析式可变形为 h,最后,求得当抛物线恰好与菱形的边AB、BC都有公共点时h的值,从而可得到h的取值范围.
【解答】
解:把代入,得,.
由解得.
抛物线的顶点在直线上,
如图1,当抛物线经过点C时,抛物线恰好与BC,AB均有交点,
将点代入,得,解得或舍去.
如图2,当抛物线经过点B时,抛物线恰好与BC,AB均有交点,
此时点B恰好为抛物线的顶点,.
综上,当时,抛物线与菱形的边AB,BC都有公共点.
21.【答案】解:根据题意得,y与x的函数关系式为
;
当时,,
解得,不合题意舍去;
故当该专卖店每件童装降价10元时,平均每天盈利400元;
该专卖店不可能平均每天盈利600元;
当时,,
整理得,
,
方程没有实数根,
即该专卖店不可能平均每天盈利600元.
【解析】本题主要考查二次函数的应用、一元二次方程的实际应用,理解题意找到题目蕴含的等量关系是列方程求解的关键.
根据总利润每件利润销售数量,可得y与x的函数关系式;
根据中的函数关系列方程,解方程即可求解;
根据中相等关系列方程,判断方程有无实数根即可得.
22.【答案】解:如图,
,
矩形PQMN为正方形,
,,
、,
设PN长为x厘米,则厘米,厘米,厘米,厘米,
即、,
,
,
解得.
答:当时,PN的长度是厘米;
设PN的长度是x厘米,PQ的长度是y厘米时,
四边形PQMN为矩形,
,
∽,
,,
与x之间的函数关系式为;
矩形PQMN面积
,
故当PN的长度是6厘米时,矩形零件PQMN的面积最大,最大面积为24平方厘米.
【解析】本题考查的是相似三角形的应用,矩形的性质,正方形的判定及性质,二次函数解析式的求法,平行线分线段成比例,一次函数解析式的求法,二次函数的最值和性质等有关知识,利用矩形的面积公式得到关于x的二次函数,根据二次函数的性质,确定x的取值和面积的最大值是解题关键.
当时,矩形PQMN是正方形,设PN长为x厘米,由正方形的性质得出,,根据平行线的性质,可以得出比例关系式、,,代入数据求解即可;
先证明∽,再根据相似三角形对应边的比等于对应高的比列出比例式,即可求解;
根据矩形面积公式得到关于x的二次函数,根据二次函数求出矩形的最大值.
23.【答案】解:由题意得:,,
解得:,,
则此抛物线的解析式为;
抛物线对称轴为直线,,
横坐标为,C横坐标为1,
把代入抛物线解析式得:,
,,
设直线AB解析式为,
把B坐标代入得:,即,
作出直线CP,与AB交于点Q,过Q作轴,与y轴交于点H,BC与y轴交于点M,
可得∽,
,
点P在x轴上,直线CP将面积分成2:3两部分,
::3或AQ::2,即AQ::5或AQ::5,
,
或,
当时,把代入直线AB解析式得:,
此时,直线CQ解析式为,令,得到,即;
当时,把代入直线AB解析式得:,
此时,直线CQ解析式为,令,得到,此时,
综上,P的坐标为或.
【解析】由对称轴直线,以及A点坐标确定出b与c的值,即可求出抛物线解析式;
由抛物线的对称轴及BC的长,确定出B与C的横坐标,代入抛物线解析式求出纵坐标,确定出B与C坐标,利用待定系数法求出直线AB解析式,作出直线CP,与AB交于点Q,过Q作轴,与y轴交于点H,BC与y轴交于点M,由已知面积之比求出QH的长,确定出Q横坐标,代入直线AB解析式求出纵坐标,确定出Q坐标,再利用待定系数法求出直线CQ解析式,即可确定出P的坐标.
此题考查了待定系数法求二次函数解析式,二次函数性质,以及二次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.
24.【答案】解:抛物线的图象与x轴交于,两点,与y轴交于点,
,
解得,,
即此抛物线的解析式是;
,
此抛物线顶点D的坐标是,对称轴是直线;
存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,
设点P的坐标为,
当时,
,
解得,,
即点P的坐标为;
当时,
,
解得,,
即点P的坐标为或;
当时,
,
解得,,
即点P的坐标是或,
当点P为时与点D重合,故不符合题意,
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为或或或.
【解析】本题考查二次函数综合题,解题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答问题.
根据抛物线的图象与x轴交于,两点,与y轴交于点,可以求得抛物线的解析式;
根据中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
第2页,共2页
第1页,共1页
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
