人教版五年级下册数学4.分数的意义和性质 最大公因数 教案(2课时)
文档属性
| 名称 | 人教版五年级下册数学4.分数的意义和性质 最大公因数 教案(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 78.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览



文档简介
第四单元 分数的意义和性质
课 题 第8课时最大公因数 授课类型 新授课
教学内容 最大公因数的概念和求两个数的最大公因数(教材第60页的例1、例2,第61页“做一做”及第63页练习十五的第1~4题)。
教学 目标 1.使学生理解和掌握公因数和最大公因数的概念。 2.能了解求两个数的公因数和最大公因数的方法,并能用自己喜欢的方法,找出两个数的最大公因数。 3.通过数学活动过程,训练学生思维的有序性和条理性。
教学重点 理解和掌握求公因数和最大公因数的方法,找出两个数的最大公因数。
教学难点 最大公因数的求法。
教具准备 多媒体课件
教学方法 创设情境,启发探究,合作交流。
教 学 过 程
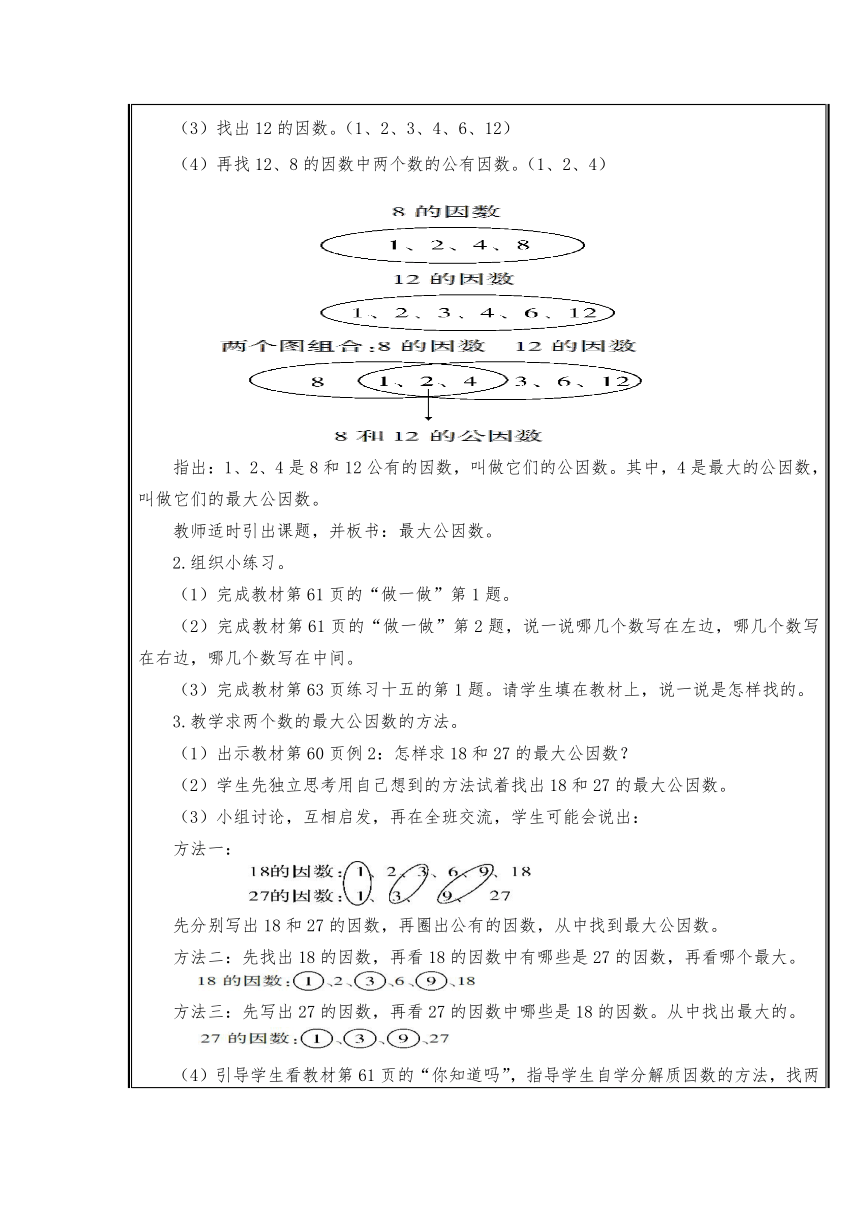
第8课时【复习导入】 1.教师提问:什么是因数?因数有什么特点? 学生回顾前面的知识,在小组中交流后汇报,老师总结使学生了解因数的几个特点: (1)最小的因数是1,最大的因数是它本身; (2)因数的个数是有限的; (3)一个数除以它的因数,商一定是自然数(0除外)。 2.写出16和12所有因数。学生独立练习,然后交流检查。 教师提问:你是怎样找一个数的因数的?(组织学生交流,再说一说) 【新课讲授】 1.教学公因数和最大公因数。 (1)出示教材第60页例1。 (2)找出8的因数。(1、2、4、8)
教 学 过 程
(3)找出12的因数。(1、2、3、4、6、12) (4)再找12、8的因数中两个数的公有因数。(1、2、4)指出:1、2、4是8和12公有的因数,叫做它们的公因数。其中,4是最大的公因数,叫做它们的最大公因数。 教师适时引出课题,并板书:最大公因数。 2.组织小练习。 (1)完成教材第61页的“做一做”第1题。 (2)完成教材第61页的“做一做”第2题,说一说哪几个数写在左边,哪几个数写在右边,哪几个数写在中间。 (3)完成教材第63页练习十五的第1题。请学生填在教材上,说一说是怎样找的。 3.教学求两个数的最大公因数的方法。 (1)出示教材第60页例2:怎样求18和27的最大公因数? (2)学生先独立思考用自己想到的方法试着找出18和27的最大公因数。 (3)小组讨论,互相启发,再在全班交流,学生可能会说出: 方法一:先分别写出18和27的因数,再圈出公有的因数,从中找到最大公因数。 方法二:先找出18的因数,再看18的因数中有哪些是27的因数,再看哪个最大。方法三:先写出27的因数,再看27的因数中哪些是18的因数。从中找出最大的。(4)引导学生看教材第61页的“你知道吗”,指导学生自学分解质因数的方法,找两个数的最大公因数。24和36的最大公因数=2×2×3=12 指出:两个数所有公因数的积,就是这两个数的最大公因数。 (5)巩固小练习:完成教材第61页的“做一做”第2、3题。 第2题:学生根据所学知识站队,并说出这样站队的道理。 第3题:学生先独立观察每组数有什么特点,再进行交流。 小结:求两个数的最大公因数有哪些特殊情况? 两个数成倍数关系时,较小的数就是它们的最大公因数。 ②当两个数只有公因数1时,它们的最大公因数也是1。 【课堂作业】 1.完成教材第63页练习十五的第2题。 学生先独立完成,然后集体交流找最大公因数的方法,并将这8组数分为三类:一类是最大的公因数是1,(如5和9,15和16);一类是最大公因数是较小的数本身(如34和17、16和48、13和78);另一类是一般情况。 2.完成教材第63页练习十五的第3题。 学生独立完成,填在课本上,集体交流。 3.完成教材第63页练习十五的第4题。 此题渗透了互质数组成的几种情况,练习时,教师可先让学生回忆质数和合数的概念,然后让学生独立完成,然后全班反馈。 【课堂小结】 通过这节课的学习活动,你有什么收获?学生畅谈学习所得。 【课后作业】 完成练习册中本课时练习。 【板书设计】 最大公因数 两个数公有的因数叫做它们的公因数;其中最大的公因数,叫做它们的最大公因数。
教学 后记
第四单元 分数的意义和性质
课 题 第9课时 利用最大公因数知识解决问题 授课类型 练习课
教学内容 利用最大公因数知识解决生活中的实际问题(教材第62页的例3,及教材第63~64页练习十五第5~11题)。
教学 目标 1.让学生进一步理解两个数的公因数和最大公因数的意义。 2.让学生能利用最大公因数知识解决生活中的实际问题。
教学重点 能正确判断生活中的实际问题是要利用最大公因数知识来解决,并能说出这样想的道理。
教学难点 能正确判断生活中的实际问题是要利用最大公因数知识来解决,并能说出这样想的道理。
教具准备 多媒体课件
教学方法 创设情境,启发探究,合作交流。
教 学 过 程
第9课时【复习导入】 1.什么是公因数?什么是最大公因数? 2.找出每组数的最大公因数。 5和15 21和28 30和18 8和9 11和33 60和48 12和42 4和15 在现实生活中,有的问题需要用最大公因数的知道来解决,这就是我们今天要学习的内容。 板书课题: 最大公因数。 【新课讲授】 出示教材第62页例3。 (1)引导学生审题,理解题意。在贮藏室的长方形地面上铺正方形地砖。要求既要铺满,又要都用整块的方砖。 (2)学生以小组为单位,探究如何拼摆。 每组4人,在课前印好画有长方形的方格纸,每人选择一种边长的方砖,试一试,只要画满一条长边,一条宽边就可以。 教师巡视指导,辅导学生。 (3)多媒体演示拼摆过程,进一步验证学生动手操作的情况。 (4)教师:应该怎样选择方砖来铺地呢? 通过交流,得出结论:要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
教 学 过 程
(5)12和16的公因数有1、2、4,其中最大公因数是4。所以可选边长是1dm、2dm、4dm的地砖,边长最大的是4dm。 【课堂作业】 完成教材第63~64页练习十五第5~11题。 1.完成教材第63页练习十五的第5题。 此题是有关两数最大公因数的实际问题。教师要引导学生理解题意,要剪成“同样大小的正方形而没有剩余”。正方形的边长必须既是70的因数又是50的因数,要使正方形的边长最大,所以要找70和50的最大公因数。学生弄清题意后,由学生独立完成,然后全班反馈。 2.完成教材第63页练习十五的第6题。 此题也是有关两数最大公因数的实际问题,“要使每排的人数相等”则每排的人数必须既是48,又是36的因数,要使每排的人数最多,所以要找48和36的最大公因数,学生理解题意即可完成。 3.完成教材第64页练习十五第7题。 此题求两个数的最大公因数。 4.完成教材第64页练习十五第8题。 此题检验学生公因数是1的数的几种情况,答案不唯一。 5.完成教材第64页练习十五第9题此题检查学生当两数是倍数关系、互质关系、一般关系情况下求最大公因数的能力。 6.完成教材第64页练习十五第10题 填表找规律. 7.完成教材第64页练习十五的第11题。 这一题是有关三个数最大公因数的实际问题。教师要引导学生理解题意,要达到“截成同样长的小棒,不能有剩余”的要求,每根小棒的长必须是12、16和44的公因数。要使每根小棒的长度最长,所以要找出12、16和44的最大公因数,练习时,可让学生分别写出12、16和44的因数,再从中找出它们的最大公因数。 【课堂小结】 通过这节课的学习,你有什么收获? 【课后作业】 完成练习册中本课时练习。 【板书设计】 最大公因数 几个数公有的因数叫做它们的公因数,公因数中最大的因数叫它们的最大公因数。 (1)两个数没有特殊关系,用列举法找出它们的最大公因数。 (2)两个数是倍数关系,它们的最大公因数是较小数。 (3)两个数公因数只有1,它们的最大公因数是1。
教学 后记
课 题 第8课时最大公因数 授课类型 新授课
教学内容 最大公因数的概念和求两个数的最大公因数(教材第60页的例1、例2,第61页“做一做”及第63页练习十五的第1~4题)。
教学 目标 1.使学生理解和掌握公因数和最大公因数的概念。 2.能了解求两个数的公因数和最大公因数的方法,并能用自己喜欢的方法,找出两个数的最大公因数。 3.通过数学活动过程,训练学生思维的有序性和条理性。
教学重点 理解和掌握求公因数和最大公因数的方法,找出两个数的最大公因数。
教学难点 最大公因数的求法。
教具准备 多媒体课件
教学方法 创设情境,启发探究,合作交流。
教 学 过 程
第8课时【复习导入】 1.教师提问:什么是因数?因数有什么特点? 学生回顾前面的知识,在小组中交流后汇报,老师总结使学生了解因数的几个特点: (1)最小的因数是1,最大的因数是它本身; (2)因数的个数是有限的; (3)一个数除以它的因数,商一定是自然数(0除外)。 2.写出16和12所有因数。学生独立练习,然后交流检查。 教师提问:你是怎样找一个数的因数的?(组织学生交流,再说一说) 【新课讲授】 1.教学公因数和最大公因数。 (1)出示教材第60页例1。 (2)找出8的因数。(1、2、4、8)
教 学 过 程
(3)找出12的因数。(1、2、3、4、6、12) (4)再找12、8的因数中两个数的公有因数。(1、2、4)指出:1、2、4是8和12公有的因数,叫做它们的公因数。其中,4是最大的公因数,叫做它们的最大公因数。 教师适时引出课题,并板书:最大公因数。 2.组织小练习。 (1)完成教材第61页的“做一做”第1题。 (2)完成教材第61页的“做一做”第2题,说一说哪几个数写在左边,哪几个数写在右边,哪几个数写在中间。 (3)完成教材第63页练习十五的第1题。请学生填在教材上,说一说是怎样找的。 3.教学求两个数的最大公因数的方法。 (1)出示教材第60页例2:怎样求18和27的最大公因数? (2)学生先独立思考用自己想到的方法试着找出18和27的最大公因数。 (3)小组讨论,互相启发,再在全班交流,学生可能会说出: 方法一:先分别写出18和27的因数,再圈出公有的因数,从中找到最大公因数。 方法二:先找出18的因数,再看18的因数中有哪些是27的因数,再看哪个最大。方法三:先写出27的因数,再看27的因数中哪些是18的因数。从中找出最大的。(4)引导学生看教材第61页的“你知道吗”,指导学生自学分解质因数的方法,找两个数的最大公因数。24和36的最大公因数=2×2×3=12 指出:两个数所有公因数的积,就是这两个数的最大公因数。 (5)巩固小练习:完成教材第61页的“做一做”第2、3题。 第2题:学生根据所学知识站队,并说出这样站队的道理。 第3题:学生先独立观察每组数有什么特点,再进行交流。 小结:求两个数的最大公因数有哪些特殊情况? 两个数成倍数关系时,较小的数就是它们的最大公因数。 ②当两个数只有公因数1时,它们的最大公因数也是1。 【课堂作业】 1.完成教材第63页练习十五的第2题。 学生先独立完成,然后集体交流找最大公因数的方法,并将这8组数分为三类:一类是最大的公因数是1,(如5和9,15和16);一类是最大公因数是较小的数本身(如34和17、16和48、13和78);另一类是一般情况。 2.完成教材第63页练习十五的第3题。 学生独立完成,填在课本上,集体交流。 3.完成教材第63页练习十五的第4题。 此题渗透了互质数组成的几种情况,练习时,教师可先让学生回忆质数和合数的概念,然后让学生独立完成,然后全班反馈。 【课堂小结】 通过这节课的学习活动,你有什么收获?学生畅谈学习所得。 【课后作业】 完成练习册中本课时练习。 【板书设计】 最大公因数 两个数公有的因数叫做它们的公因数;其中最大的公因数,叫做它们的最大公因数。
教学 后记
第四单元 分数的意义和性质
课 题 第9课时 利用最大公因数知识解决问题 授课类型 练习课
教学内容 利用最大公因数知识解决生活中的实际问题(教材第62页的例3,及教材第63~64页练习十五第5~11题)。
教学 目标 1.让学生进一步理解两个数的公因数和最大公因数的意义。 2.让学生能利用最大公因数知识解决生活中的实际问题。
教学重点 能正确判断生活中的实际问题是要利用最大公因数知识来解决,并能说出这样想的道理。
教学难点 能正确判断生活中的实际问题是要利用最大公因数知识来解决,并能说出这样想的道理。
教具准备 多媒体课件
教学方法 创设情境,启发探究,合作交流。
教 学 过 程
第9课时【复习导入】 1.什么是公因数?什么是最大公因数? 2.找出每组数的最大公因数。 5和15 21和28 30和18 8和9 11和33 60和48 12和42 4和15 在现实生活中,有的问题需要用最大公因数的知道来解决,这就是我们今天要学习的内容。 板书课题: 最大公因数。 【新课讲授】 出示教材第62页例3。 (1)引导学生审题,理解题意。在贮藏室的长方形地面上铺正方形地砖。要求既要铺满,又要都用整块的方砖。 (2)学生以小组为单位,探究如何拼摆。 每组4人,在课前印好画有长方形的方格纸,每人选择一种边长的方砖,试一试,只要画满一条长边,一条宽边就可以。 教师巡视指导,辅导学生。 (3)多媒体演示拼摆过程,进一步验证学生动手操作的情况。 (4)教师:应该怎样选择方砖来铺地呢? 通过交流,得出结论:要使所用的正方形地砖都是整块的,地砖的边长必须既是16的因数,又是12的因数。
教 学 过 程
(5)12和16的公因数有1、2、4,其中最大公因数是4。所以可选边长是1dm、2dm、4dm的地砖,边长最大的是4dm。 【课堂作业】 完成教材第63~64页练习十五第5~11题。 1.完成教材第63页练习十五的第5题。 此题是有关两数最大公因数的实际问题。教师要引导学生理解题意,要剪成“同样大小的正方形而没有剩余”。正方形的边长必须既是70的因数又是50的因数,要使正方形的边长最大,所以要找70和50的最大公因数。学生弄清题意后,由学生独立完成,然后全班反馈。 2.完成教材第63页练习十五的第6题。 此题也是有关两数最大公因数的实际问题,“要使每排的人数相等”则每排的人数必须既是48,又是36的因数,要使每排的人数最多,所以要找48和36的最大公因数,学生理解题意即可完成。 3.完成教材第64页练习十五第7题。 此题求两个数的最大公因数。 4.完成教材第64页练习十五第8题。 此题检验学生公因数是1的数的几种情况,答案不唯一。 5.完成教材第64页练习十五第9题此题检查学生当两数是倍数关系、互质关系、一般关系情况下求最大公因数的能力。 6.完成教材第64页练习十五第10题 填表找规律. 7.完成教材第64页练习十五的第11题。 这一题是有关三个数最大公因数的实际问题。教师要引导学生理解题意,要达到“截成同样长的小棒,不能有剩余”的要求,每根小棒的长必须是12、16和44的公因数。要使每根小棒的长度最长,所以要找出12、16和44的最大公因数,练习时,可让学生分别写出12、16和44的因数,再从中找出它们的最大公因数。 【课堂小结】 通过这节课的学习,你有什么收获? 【课后作业】 完成练习册中本课时练习。 【板书设计】 最大公因数 几个数公有的因数叫做它们的公因数,公因数中最大的因数叫它们的最大公因数。 (1)两个数没有特殊关系,用列举法找出它们的最大公因数。 (2)两个数是倍数关系,它们的最大公因数是较小数。 (3)两个数公因数只有1,它们的最大公因数是1。
教学 后记
