第1课时 加、减法的意义和各部分间的关系 16张PPT
文档属性
| 名称 | 第1课时 加、减法的意义和各部分间的关系 16张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 19:59:24 | ||
图片预览





文档简介
课件16张PPT。人教版数学四年级下册 第一单元情境导入探究新知拓展练习课堂小结数学阅读加、减法的意义和
各部分间的关系基础练习青藏铁路是世界上最长的高原
铁路,穿越了“世界屋脊”青
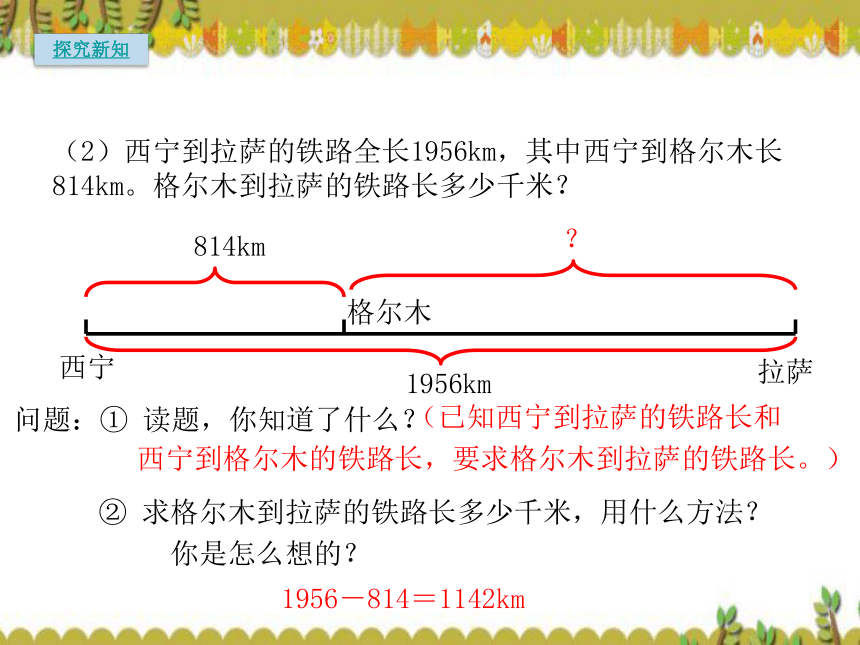
藏高原,到达圣地—拉萨!情境导入情境导入拉萨到西宁的铁路长1956km。根据图中的信息提出用加法、减法解决的问题。探究新知(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。格尔木到拉萨的铁路长多少千米?(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米?要求:先画出线段图,再列式解答。探究新知(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?把两个数合并成一个数的运算,叫做加法814+1142=1956(km)相加的两个数叫做加数,加得的数叫做和。加数加数和探究新知(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。格尔木到拉萨的铁路长多少千米?1956km?② 求格尔木到拉萨的铁路长多少千米,用什么方法?
你是怎么想的?1956-814=1142km问题:① 读题,你知道了什么? (已知西宁到拉萨的铁路长和
西宁到格尔木的铁路长,要求格尔木到拉萨的铁路长。)
探究新知(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米??19561142问题:求西宁到格尔木的铁路长多少千米,用什么方法?你是怎么想的?1956-1142=814km探究新知问题:与第(1)题相比,第(2)、(3)题分别是已知什么?求什么?怎样算?814+1142=19561956-814=11421956-1142=814(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。格尔木到拉萨的铁路长多少千米?(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米?探究新知问题:用你自己的话说一说,你认为什么是减法?814+1142=19561956-814=11421956-1142=814已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。在减法中,已知的和叫做被减数……1956-814=11421956-1142=814被减数减数差探究新知1. 加法各部分间的关系:和=加数+加数加数=和-另一个加数加、减法各部分间的关系2. 减法各部分间的关系:差=被减数-减数问题:如果知道被减数和差,能求出减数吗?减数=被减数-差问题:如果知道减数和差,能求出被减数吗?被减数=减数+差问题:如果知道和与一个加数,能求出另一个加数吗?减法是加法的逆运算!探究新知201+ =300 +193=258
860 - =237 -587=1211.说说下面算式中方框里的数怎么求,依据是什么?并计算出结果。9965623708基础练习2.根据加、减法各部分间的关系,写出另外两个等式。350-147=203350-203=14755+12=6767-12=55239+611=850850-611=239拓展练习填一填。200+=654-=500200651154357530拓展练习数学阅读8岁的高斯发现数学定理
德国著名大科学家高斯(1777~1855)出生在一个贫穷的家庭。
有一天高斯的数学教师对同学们说:“谁能替我算从1加2加3一直到100的和?”结果不到半个小时,小高斯拿起了他的石板走上前去。“老师,答案是不是这样?”老师头也不抬,挥着那肥厚的手,说:“去,回去再算!错了。”
高斯解释他发现的一个方法,这个方法就是古时希腊人和中国人用来计算级数1+2+3+…+n的方法。高斯的发现使老师觉得羞愧,觉得自己轻视穷人家的孩子的观点是不对的。他以后也认真教起书来,并且还常从城里买些数学书给高斯看。在他的鼓励下,高斯在后期的数学研究上取得了很高的成就。8岁的高斯发现数学定理
德国著名大科学家高斯(1777~1855)出生在一个贫穷的家庭。有一天高斯的数学教师对同学们说:“你们今天替我算从1加2加3一直到100的和。”结果不到半个小时,小高斯拿起了他的石板走上前去。“老师,答案是不是这样?”老师头也不抬,挥着那肥厚的手,说:“去,回去再算!错了。”高斯却站着不动,把石板伸向老师面前:“老师!我想这个答案是对的。”
高斯解释他发现的一个方法,这个方法就是古时希腊人和中国人用来计算级数1+2+3+…+n的方法。高斯的发现使老师觉得羞愧,。他以后常从城里买些数学书给高斯看。在他的鼓励下,高斯在后期的数学研究上取得了很高的成就。课堂小结你学到了
什么?
铁路,穿越了“世界屋脊”青
藏高原,到达圣地—拉萨!情境导入情境导入拉萨到西宁的铁路长1956km。根据图中的信息提出用加法、减法解决的问题。探究新知(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。格尔木到拉萨的铁路长多少千米?(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米?要求:先画出线段图,再列式解答。探究新知(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?把两个数合并成一个数的运算,叫做加法814+1142=1956(km)相加的两个数叫做加数,加得的数叫做和。加数加数和探究新知(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木长814km。格尔木到拉萨的铁路长多少千米?1956km?② 求格尔木到拉萨的铁路长多少千米,用什么方法?
你是怎么想的?1956-814=1142km问题:① 读题,你知道了什么? (已知西宁到拉萨的铁路长和
西宁到格尔木的铁路长,要求格尔木到拉萨的铁路长。)
探究新知(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米??19561142问题:求西宁到格尔木的铁路长多少千米,用什么方法?你是怎么想的?1956-1142=814km探究新知问题:与第(1)题相比,第(2)、(3)题分别是已知什么?求什么?怎样算?814+1142=19561956-814=11421956-1142=814(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。西宁到拉萨的铁路长多少千米?(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。格尔木到拉萨的铁路长多少千米?(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。西宁到格尔木的铁路长多少千米?探究新知问题:用你自己的话说一说,你认为什么是减法?814+1142=19561956-814=11421956-1142=814已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。在减法中,已知的和叫做被减数……1956-814=11421956-1142=814被减数减数差探究新知1. 加法各部分间的关系:和=加数+加数加数=和-另一个加数加、减法各部分间的关系2. 减法各部分间的关系:差=被减数-减数问题:如果知道被减数和差,能求出减数吗?减数=被减数-差问题:如果知道减数和差,能求出被减数吗?被减数=减数+差问题:如果知道和与一个加数,能求出另一个加数吗?减法是加法的逆运算!探究新知201+ =300 +193=258
860 - =237 -587=1211.说说下面算式中方框里的数怎么求,依据是什么?并计算出结果。9965623708基础练习2.根据加、减法各部分间的关系,写出另外两个等式。350-147=203350-203=14755+12=6767-12=55239+611=850850-611=239拓展练习填一填。200+=654-=500200651154357530拓展练习数学阅读8岁的高斯发现数学定理
德国著名大科学家高斯(1777~1855)出生在一个贫穷的家庭。
有一天高斯的数学教师对同学们说:“谁能替我算从1加2加3一直到100的和?”结果不到半个小时,小高斯拿起了他的石板走上前去。“老师,答案是不是这样?”老师头也不抬,挥着那肥厚的手,说:“去,回去再算!错了。”
高斯解释他发现的一个方法,这个方法就是古时希腊人和中国人用来计算级数1+2+3+…+n的方法。高斯的发现使老师觉得羞愧,觉得自己轻视穷人家的孩子的观点是不对的。他以后也认真教起书来,并且还常从城里买些数学书给高斯看。在他的鼓励下,高斯在后期的数学研究上取得了很高的成就。8岁的高斯发现数学定理
德国著名大科学家高斯(1777~1855)出生在一个贫穷的家庭。有一天高斯的数学教师对同学们说:“你们今天替我算从1加2加3一直到100的和。”结果不到半个小时,小高斯拿起了他的石板走上前去。“老师,答案是不是这样?”老师头也不抬,挥着那肥厚的手,说:“去,回去再算!错了。”高斯却站着不动,把石板伸向老师面前:“老师!我想这个答案是对的。”
高斯解释他发现的一个方法,这个方法就是古时希腊人和中国人用来计算级数1+2+3+…+n的方法。高斯的发现使老师觉得羞愧,。他以后常从城里买些数学书给高斯看。在他的鼓励下,高斯在后期的数学研究上取得了很高的成就。课堂小结你学到了
什么?
