苏科版八年级数学上册 第六章 一次函数真题专题复习练习 (三)(无答案)
文档属性
| 名称 | 苏科版八年级数学上册 第六章 一次函数真题专题复习练习 (三)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 00:00:00 | ||
图片预览



文档简介
一次函数专题复习(三)
考点九、一次函数与不等式
【典型例题】
【例9】若一次函数的图象如图所示,点在函数图象上,则关于x的不等式的解集是______.
1.【答案】
【解析】解法1:直线的图象经过点和,
,
解得,
一次函数解析式为,
当时,解得;
解法2:点在一次函数的图象上,则
当时,,
故关于x的不等式的解集为点P及其左侧部分图象对应的横坐标的集合,
的横坐标为3,
不等式的解集为:.
故答案为:
先根据待定系数法求得一次函数解析式,再解关于x的一元一次不等式即可.
本题主要考查了一次函数与一元一次不等式的关系,解决此类试题时注意:一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数的值大于或小于的自变量x的取值范围;从函数图象的角度看,就是确定直线在x轴上或下方部分所有的点的横坐标所构成的集合.
【强化练习】
1.如图,直线与相交于点P,若点P的横坐标为,则关于x的不等式的解集是
B.
C.
D.
2.如图:与:相交于点,则关于x的不等式的解为
A.
B.
C.
D.
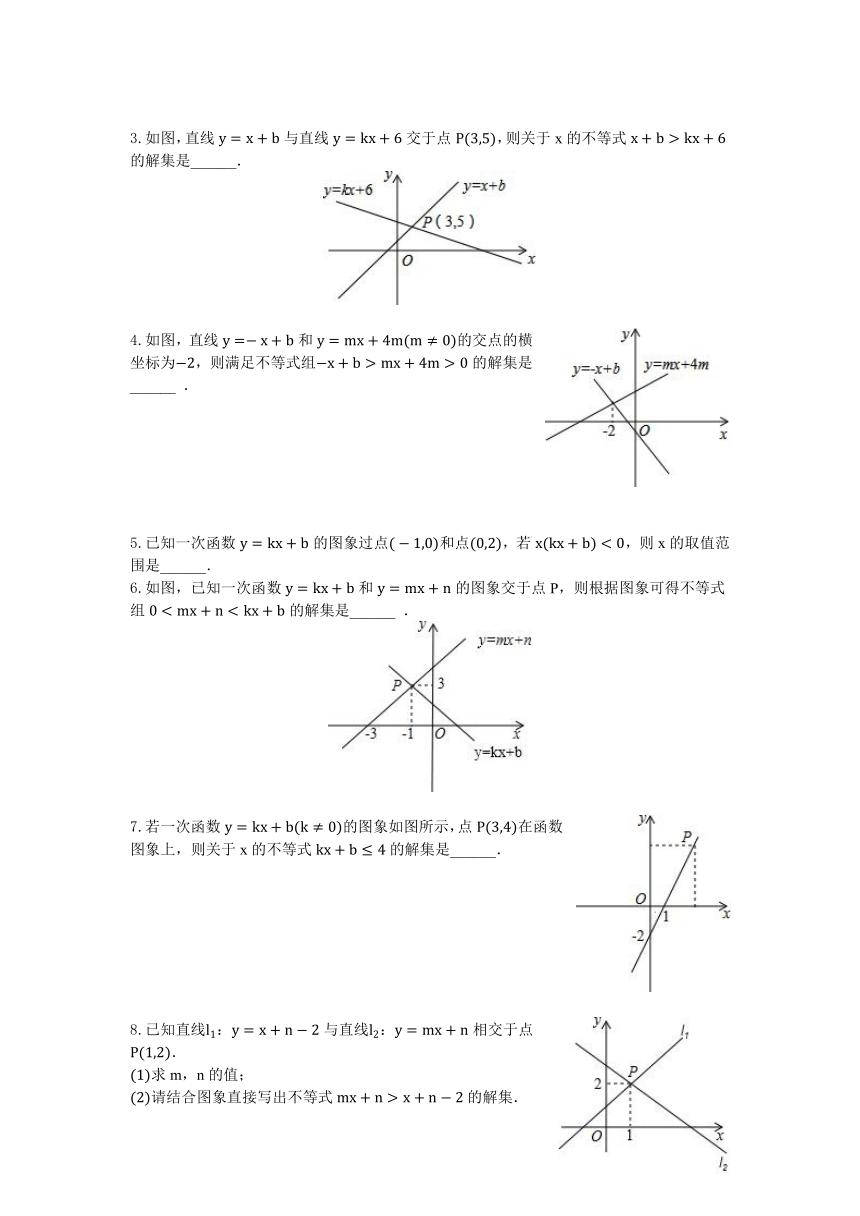
3.如图,直线与直线交于点,则关于x的不等式的解集是______.
4.如图,直线和的交点的横坐标为,则满足不等式组的解集是______ .
5.已知一次函数的图象过点和点,若,则x的取值范围是______.
6.如图,已知一次函数和的图象交于点P,则根据图象可得不等式组的解集是______ .
7.若一次函数的图象如图所示,点在函数图象上,则关于x的不等式的解集是______.
8.已知直线:与直线:相交于点.
求m,n的值;
请结合图象直接写出不等式的解集.
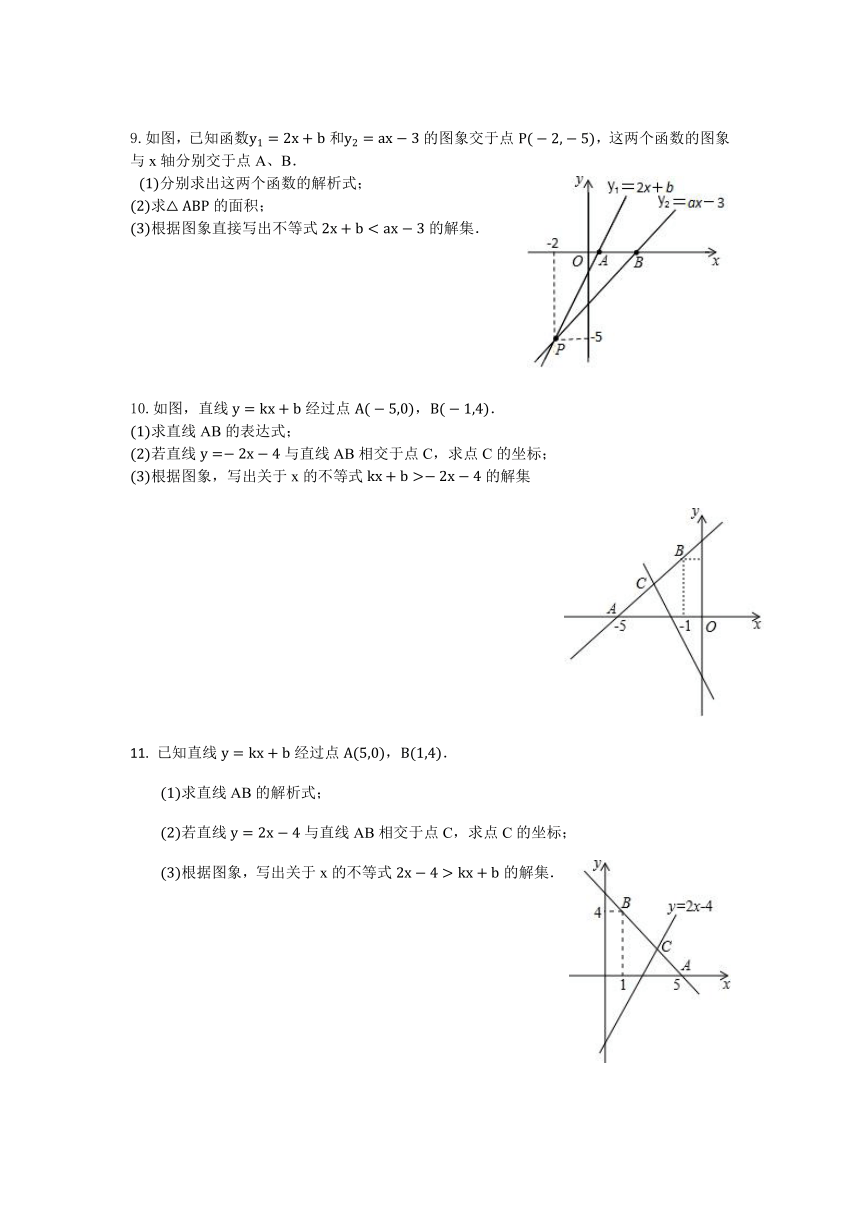
9.如图,已知函数和的图象交于点,这两个函数的图象与x轴分别交于点A、B.
分别求出这两个函数的解析式;
求的面积;
根据图象直接写出不等式的解集.
10.如图,直线经过点,.
求直线AB的表达式;
若直线与直线AB相交于点C,求点C的坐标;
根据图象,写出关于x的不等式的解集
已知直线经过点,.
求直线AB的解析式;
若直线与直线AB相交于点C,求点C的坐标;
根据图象,写出关于x的不等式的解集.
考点十、一次函数的面积
【典型例题】
【例10】如果直线与两坐标轴所围成的三角形面积是9,则b的值为______.
【解析】【分析】
本题考查了绝对值、一次函数图像、一次函数图象上点的坐标特征、三角形的面积等知识点;
求出函数与x轴、y轴的交点是解题的关键.
先求出直线与两坐标轴的交点,再根据三角形的面积公式列出关于b的方程,
出b的值即可.
【解答】
解:当时,,
当时,,
则根据三角形的面积公式:,
解得;
故答案为:.
【强化练习】
1.经过点且与坐标轴围成的三角形面积为2的直线解析式是______ .
2.如图,已知一次函数的图象经过,两点,并且交x轴于点C,交y轴于点D.
求该一次函数的解析式;
求的面积.
3.已知一次函数的图象经过点和点.
求此一次函数的解析式;
若一次函数的图象与x轴相交于点C,求点C的坐标;
求的面积.
4.如图,过点的两条直线,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知.
求点B的坐标;
若的面积为4,求直线的解析式.
5.如图,正比例函数的图象与一次函数的图象交于点,一次函数图象经过点,与y轴的交点为C,与x轴的交点为D.
求一次函数解析式;
求的面积.
如图,在平面直角坐标系中,一次函数的图象与x轴交点为,与y轴交点为B,且与正比例函数的图象交于点.
求m的值及一次函数的表达式;
若点P是y轴上一点,且的面积为6,请求出点P的坐标.
考点十一、一次函数与几何最小值
【典型例题】
【例11】如图,直线与x轴、y轴分别交于点A和点B,x轴上有一点,点P为直线一动点,当值最小时点P的坐标为______.
【解析】【分析】
本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.作点C关于直线的对称点,连接,交直线于点P,则点P即为所求.求出AB两点的坐标,据此可得出及的度数,根据轴对称的性质得出是等腰直角三角形,故可得出点的坐标,利用待定系数法求出直线的坐标,进而可得出P点坐标.
【解答】
解:如图,作点C关于直线的对称点,连接,
交直线于点P,则点P即为所求,
直线与x轴、y轴分别交于点A和点B,
,,
.
点C,关于直线AB对称,
是线段的垂直平分线,
是等腰直角三角形,.
,
.
设直线的解析式为,则,解得,
直线的解析式为,
,解得,
故答案为
【强化练习】
1.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当最小时,点P的坐标为
A. B.
C. D.
2.在如图所示的平面直角坐标系中,点P是直线上的动点,,是x轴上的两点,则的最小值为______.
3.如图,直线:与x轴相交于点A,直线:经过点,与x轴交于点,与y轴交于点C,与直线相交于点D.
求直线的函数关系式;
点P是上的一点,若的面积等于的面积的2倍,求点P的坐标;
设点Q的坐标为,是否存在m的值使得最小?若存在,请求出点Q的坐标;若不存在,请说明理由.
4如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且,,点C为AB的中点,直线CD交x轴于点F.
求直线CD的函数关系式;
过点C作且交于点E,求证:;
求点E坐标;
点P是直线CE上的一个动点,求的最小值.
考点十二、一次函数中路程问题
【典型例题】
【例12】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离千米与甲车行驶时间小时之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
,B两城相距____________千米;
分别求甲、乙两车离开A城的距离y与x的关系式.
求乙车出发后几小时追上甲车?
【答案】解:
300千米;? ? ? ? ? ? ? ? ? ? ? ?
设甲对应的函数解析式为:,,
解得,,即甲对应的函数解析式为:,
设乙对应的函数解析式为,.
解得:,,即乙对应的函数解析式为;? ?
解方程组得:,,
即乙车出发后小时追上甲车.
【解析】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答。
根据函数图象可以解答本题;
根据图象中的信息分别求出甲乙两车对应的函数解析式,
根据甲乙两车对应的函数解析式,然后令它们相等即可解答本题;
【强化练习】
1.小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行他们的路程差米与小明出发时间分之间的函数关系如图所示下列说法:
小华先到达青少年宫;小华的速度是小明速度的倍;;
其中正确的是
A. B. C. D.
2.甲、乙两车从A城出发匀速行驶至B城在整个行驶过程中,甲、乙两车离开A城的距离千米与甲车行驶的时间小时之间的函数关系如图所示则下列结论:,B两城相距300千米;
乙车比甲车晚出发1小时,却早到1小时;
乙车出发后小时追上甲车;?
当甲、乙两车相距50千米时,或.
其中正确的结论有????
A. 1个 B. 2个 C. 3个 D. 4个
3.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了甲车休息前后的速度相同,甲、乙两车行驶的路程与行驶的时间的函数图象如图所示.根据图象的信息有如下四个说法:
甲车行驶40千米开始休息
乙车行驶小时与甲车相遇
甲车比乙车晚小时到到B地
两车相距50km时乙车行驶了小时
其中正确的说法有
A. 1个 B. 2个 C. 3个 D. 4个
4.已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为千米,甲行驶的时间为小时,若s与t的函数关系如图所示,则下列说法错误的是
A. 经过2小时两人相遇
B. 若乙行驶的路程是甲的2倍,则
C. 当乙到达终点时,甲离终点还有60千米
D. 若两人相距90千米,则或
5.快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地.快慢两车距各自出发地的路程千米与所用的时间时的关系如图所示,下列说法正确的有
快车返回的速度为140千米时;???
慢车的速度为70千米时;???
出发小时时,快慢两车距各自出发地的路程相等;
快慢两车出发小时时相距150千米.
A. 1个 B. 2个 C. 3个 D. 4个
6.一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离米与小玲从家出发后步行的时间分之间的关系如图所示小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计当妈妈刚回到家时,小玲离学校的距离为______米.
7.“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米分的速度骑行一段时间,休息了5分钟,再以m米分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程米与时间分钟的关系如图,请结合图象,解答下列问题:
______,______,______;
若小军的速度是120米分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
在的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?若小军的行驶速度是v米分,且在途中与爸爸恰好相遇两次不包括家、图书馆两地,请直接写出v的取值范围.
8.甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离千米与时间分钟的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
甲、乙两车行驶时的速度分别为多少?
乙车出发多少分钟后第一次与甲车相遇?
甲车中途因故障停止行驶的时间为多少分钟?
9.已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离千米与行驶时间小时之间的函数图象.
求甲车离出发地的距离千米与行驶时间小时之间的函数关系式,并写出自变量的取值范围;
若已知乙车行驶的速度是40千米小时,求出发后多长时间,两车离各自出发地的距离相等;
在上述条件下,直接写出它们在行驶过程中相遇时的时间.
考点九、一次函数与不等式
【典型例题】
【例9】若一次函数的图象如图所示,点在函数图象上,则关于x的不等式的解集是______.
1.【答案】
【解析】解法1:直线的图象经过点和,
,
解得,
一次函数解析式为,
当时,解得;
解法2:点在一次函数的图象上,则
当时,,
故关于x的不等式的解集为点P及其左侧部分图象对应的横坐标的集合,
的横坐标为3,
不等式的解集为:.
故答案为:
先根据待定系数法求得一次函数解析式,再解关于x的一元一次不等式即可.
本题主要考查了一次函数与一元一次不等式的关系,解决此类试题时注意:一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数的值大于或小于的自变量x的取值范围;从函数图象的角度看,就是确定直线在x轴上或下方部分所有的点的横坐标所构成的集合.
【强化练习】
1.如图,直线与相交于点P,若点P的横坐标为,则关于x的不等式的解集是
B.
C.
D.
2.如图:与:相交于点,则关于x的不等式的解为
A.
B.
C.
D.
3.如图,直线与直线交于点,则关于x的不等式的解集是______.
4.如图,直线和的交点的横坐标为,则满足不等式组的解集是______ .
5.已知一次函数的图象过点和点,若,则x的取值范围是______.
6.如图,已知一次函数和的图象交于点P,则根据图象可得不等式组的解集是______ .
7.若一次函数的图象如图所示,点在函数图象上,则关于x的不等式的解集是______.
8.已知直线:与直线:相交于点.
求m,n的值;
请结合图象直接写出不等式的解集.
9.如图,已知函数和的图象交于点,这两个函数的图象与x轴分别交于点A、B.
分别求出这两个函数的解析式;
求的面积;
根据图象直接写出不等式的解集.
10.如图,直线经过点,.
求直线AB的表达式;
若直线与直线AB相交于点C,求点C的坐标;
根据图象,写出关于x的不等式的解集
已知直线经过点,.
求直线AB的解析式;
若直线与直线AB相交于点C,求点C的坐标;
根据图象,写出关于x的不等式的解集.
考点十、一次函数的面积
【典型例题】
【例10】如果直线与两坐标轴所围成的三角形面积是9,则b的值为______.
【解析】【分析】
本题考查了绝对值、一次函数图像、一次函数图象上点的坐标特征、三角形的面积等知识点;
求出函数与x轴、y轴的交点是解题的关键.
先求出直线与两坐标轴的交点,再根据三角形的面积公式列出关于b的方程,
出b的值即可.
【解答】
解:当时,,
当时,,
则根据三角形的面积公式:,
解得;
故答案为:.
【强化练习】
1.经过点且与坐标轴围成的三角形面积为2的直线解析式是______ .
2.如图,已知一次函数的图象经过,两点,并且交x轴于点C,交y轴于点D.
求该一次函数的解析式;
求的面积.
3.已知一次函数的图象经过点和点.
求此一次函数的解析式;
若一次函数的图象与x轴相交于点C,求点C的坐标;
求的面积.
4.如图,过点的两条直线,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知.
求点B的坐标;
若的面积为4,求直线的解析式.
5.如图,正比例函数的图象与一次函数的图象交于点,一次函数图象经过点,与y轴的交点为C,与x轴的交点为D.
求一次函数解析式;
求的面积.
如图,在平面直角坐标系中,一次函数的图象与x轴交点为,与y轴交点为B,且与正比例函数的图象交于点.
求m的值及一次函数的表达式;
若点P是y轴上一点,且的面积为6,请求出点P的坐标.
考点十一、一次函数与几何最小值
【典型例题】
【例11】如图,直线与x轴、y轴分别交于点A和点B,x轴上有一点,点P为直线一动点,当值最小时点P的坐标为______.
【解析】【分析】
本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.作点C关于直线的对称点,连接,交直线于点P,则点P即为所求.求出AB两点的坐标,据此可得出及的度数,根据轴对称的性质得出是等腰直角三角形,故可得出点的坐标,利用待定系数法求出直线的坐标,进而可得出P点坐标.
【解答】
解:如图,作点C关于直线的对称点,连接,
交直线于点P,则点P即为所求,
直线与x轴、y轴分别交于点A和点B,
,,
.
点C,关于直线AB对称,
是线段的垂直平分线,
是等腰直角三角形,.
,
.
设直线的解析式为,则,解得,
直线的解析式为,
,解得,
故答案为
【强化练习】
1.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当最小时,点P的坐标为
A. B.
C. D.
2.在如图所示的平面直角坐标系中,点P是直线上的动点,,是x轴上的两点,则的最小值为______.
3.如图,直线:与x轴相交于点A,直线:经过点,与x轴交于点,与y轴交于点C,与直线相交于点D.
求直线的函数关系式;
点P是上的一点,若的面积等于的面积的2倍,求点P的坐标;
设点Q的坐标为,是否存在m的值使得最小?若存在,请求出点Q的坐标;若不存在,请说明理由.
4如图,正方形ABOD的边长为2,OB在x轴上,OD在y轴上,且,,点C为AB的中点,直线CD交x轴于点F.
求直线CD的函数关系式;
过点C作且交于点E,求证:;
求点E坐标;
点P是直线CE上的一个动点,求的最小值.
考点十二、一次函数中路程问题
【典型例题】
【例12】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离千米与甲车行驶时间小时之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
,B两城相距____________千米;
分别求甲、乙两车离开A城的距离y与x的关系式.
求乙车出发后几小时追上甲车?
【答案】解:
300千米;? ? ? ? ? ? ? ? ? ? ? ?
设甲对应的函数解析式为:,,
解得,,即甲对应的函数解析式为:,
设乙对应的函数解析式为,.
解得:,,即乙对应的函数解析式为;? ?
解方程组得:,,
即乙车出发后小时追上甲车.
【解析】本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答。
根据函数图象可以解答本题;
根据图象中的信息分别求出甲乙两车对应的函数解析式,
根据甲乙两车对应的函数解析式,然后令它们相等即可解答本题;
【强化练习】
1.小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行他们的路程差米与小明出发时间分之间的函数关系如图所示下列说法:
小华先到达青少年宫;小华的速度是小明速度的倍;;
其中正确的是
A. B. C. D.
2.甲、乙两车从A城出发匀速行驶至B城在整个行驶过程中,甲、乙两车离开A城的距离千米与甲车行驶的时间小时之间的函数关系如图所示则下列结论:,B两城相距300千米;
乙车比甲车晚出发1小时,却早到1小时;
乙车出发后小时追上甲车;?
当甲、乙两车相距50千米时,或.
其中正确的结论有????
A. 1个 B. 2个 C. 3个 D. 4个
3.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了甲车休息前后的速度相同,甲、乙两车行驶的路程与行驶的时间的函数图象如图所示.根据图象的信息有如下四个说法:
甲车行驶40千米开始休息
乙车行驶小时与甲车相遇
甲车比乙车晚小时到到B地
两车相距50km时乙车行驶了小时
其中正确的说法有
A. 1个 B. 2个 C. 3个 D. 4个
4.已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为千米,甲行驶的时间为小时,若s与t的函数关系如图所示,则下列说法错误的是
A. 经过2小时两人相遇
B. 若乙行驶的路程是甲的2倍,则
C. 当乙到达终点时,甲离终点还有60千米
D. 若两人相距90千米,则或
5.快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地.快慢两车距各自出发地的路程千米与所用的时间时的关系如图所示,下列说法正确的有
快车返回的速度为140千米时;???
慢车的速度为70千米时;???
出发小时时,快慢两车距各自出发地的路程相等;
快慢两车出发小时时相距150千米.
A. 1个 B. 2个 C. 3个 D. 4个
6.一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离米与小玲从家出发后步行的时间分之间的关系如图所示小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计当妈妈刚回到家时,小玲离学校的距离为______米.
7.“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米分的速度骑行一段时间,休息了5分钟,再以m米分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程米与时间分钟的关系如图,请结合图象,解答下列问题:
______,______,______;
若小军的速度是120米分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
在的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?若小军的行驶速度是v米分,且在途中与爸爸恰好相遇两次不包括家、图书馆两地,请直接写出v的取值范围.
8.甲、乙两车都从A地前往B地,如图分别表示甲、乙两车离A地的距离千米与时间分钟的函数关系.已知甲车出发10分钟后乙车才出发,甲车中途因故停止行驶一段时间后按原速继续驶向B地,最终甲、乙两车同时到达B地,根据图中提供的信息解答下列问题:
甲、乙两车行驶时的速度分别为多少?
乙车出发多少分钟后第一次与甲车相遇?
甲车中途因故障停止行驶的时间为多少分钟?
9.已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离千米与行驶时间小时之间的函数图象.
求甲车离出发地的距离千米与行驶时间小时之间的函数关系式,并写出自变量的取值范围;
若已知乙车行驶的速度是40千米小时,求出发后多长时间,两车离各自出发地的距离相等;
在上述条件下,直接写出它们在行驶过程中相遇时的时间.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
