7.3 一元一次不等式组(要点测评+课后集训+答案)
文档属性
| 名称 | 7.3 一元一次不等式组(要点测评+课后集训+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 07:30:40 | ||
图片预览


文档简介
沪科版数学七年级下册同步课时训练
第7章 一元一次不等式与不等式组
7.3 一元一次不等式组
要点测评 基础达标
要点1 一元一次不等式的实际应用
1. 下列各不等式组中,是一元一次不等式组的有( )
① ② ③ ④ ⑤2x-8<7-x<5.
A. ①②③ B. ②③⑤ C. ③④⑤ D. ①②③⑤
2. 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )
A. B. C. D.
要点2 一元一次不等式组的解法
3. 不等式组的解集在数轴上表示正确的是( )
A B
C D
4. (1)解不等式组:
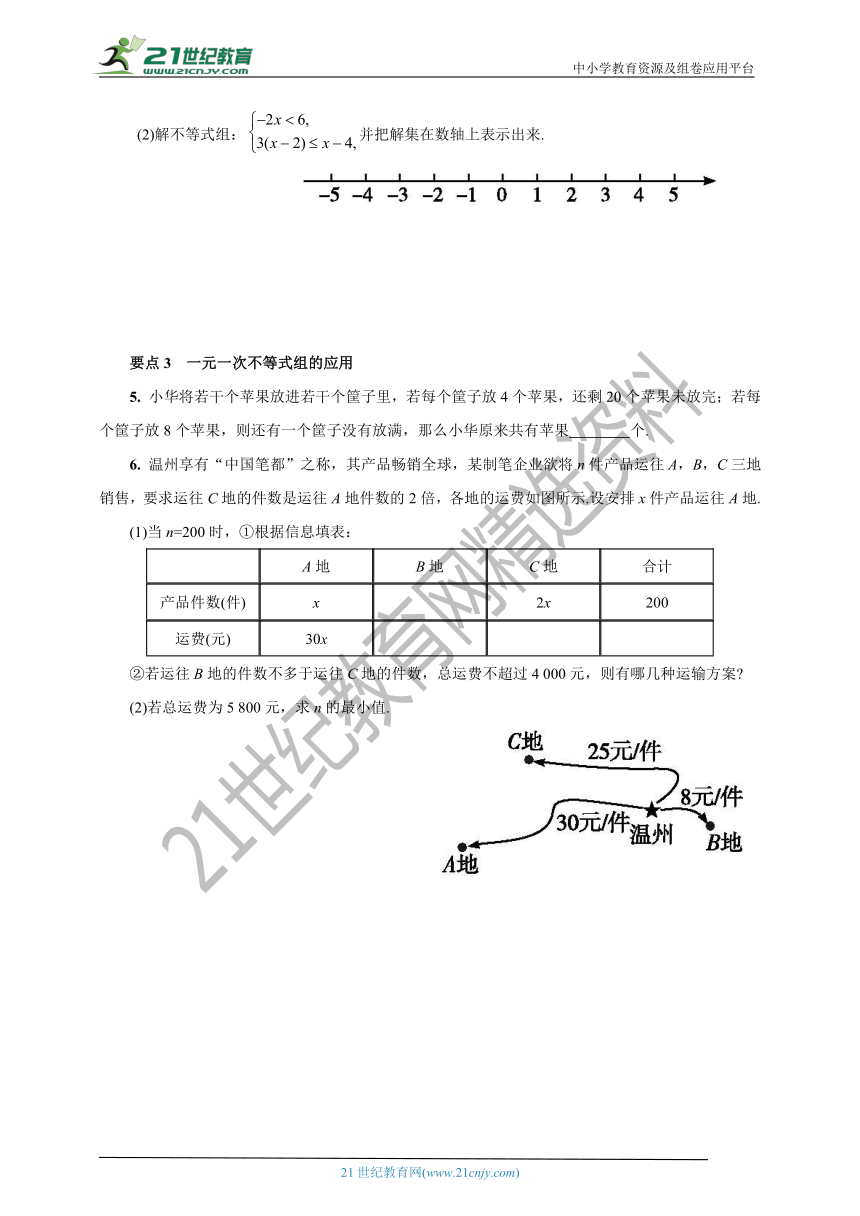
(2)解不等式组:并把解集在数轴上表示出来.
要点3 一元一次不等式组的应用
5. 小华将若干个苹果放进若干个筐子里,若每个筐子放4个苹果,还剩20个苹果未放完;若每个筐子放8个苹果,则还有一个筐子没有放满,那么小华原来共有苹果 个.?
6. 温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,①根据信息填表:
A地
B地
C地
合计
产品件数(件)
x
2x
200
运费(元)
30x
②若运往B地的件数不多于运往C地的件数,总运费不超过4 000元,则有哪几种运输方案?
(2)若总运费为5 800元,求n的最小值.
课后集训 巩固提升
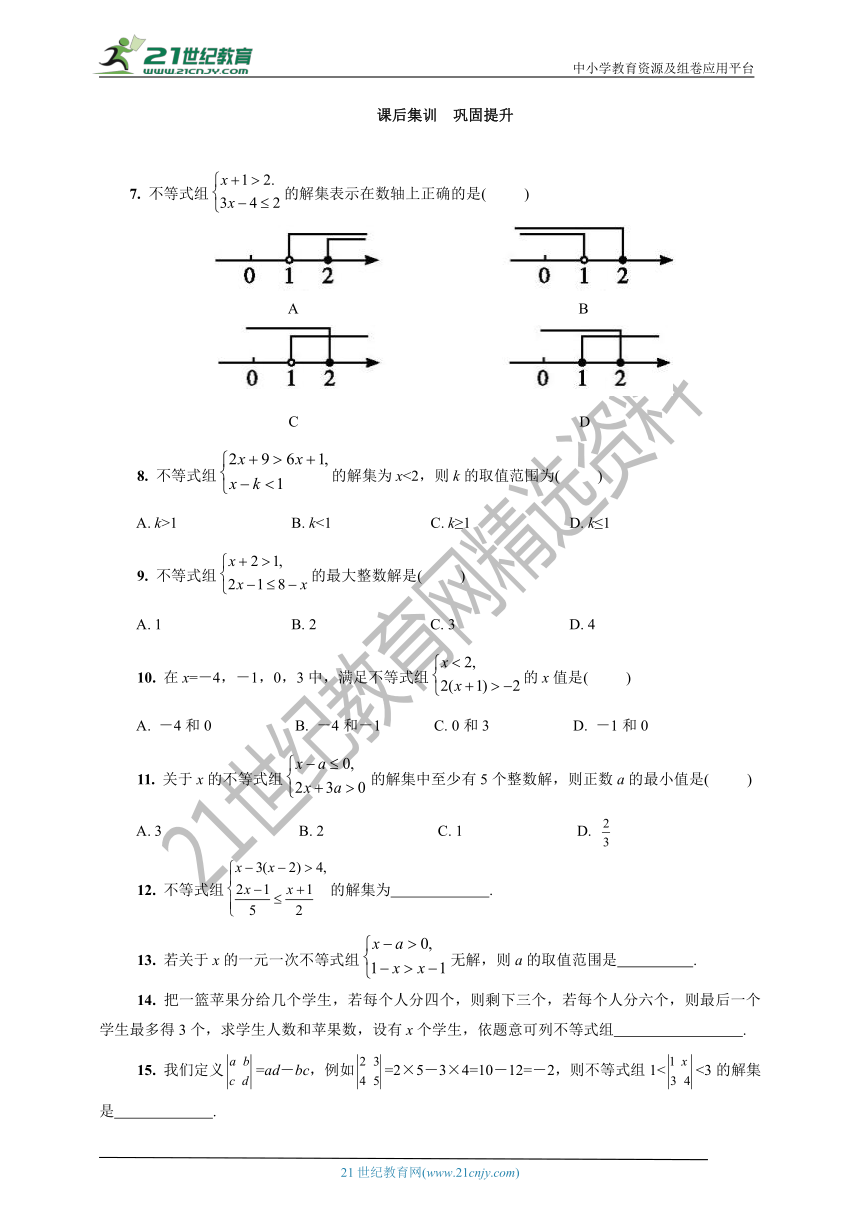
7. 不等式组的解集表示在数轴上正确的是( )
A B
C D
8. 不等式组的解集为x<2,则k的取值范围为( )
A. k>1 B. k<1 C. k≥1 D. k≤1
9. 不等式组的最大整数解是( )
A. 1 B. 2 C. 3 D. 4
10. 在x=-4,-1,0,3中,满足不等式组的x值是( )
A. -4和0 B. -4和-1 C. 0和3 D. -1和0
11. 关于x的不等式组的解集中至少有5个整数解,则正数a的最小值是( )
A. 3 B. 2 C. 1 D.
12. 不等式组的解集为 .?
13. 若关于x的一元一次不等式组无解,则a的取值范围是 .?
14. 把一篮苹果分给几个学生,若每个人分四个,则剩下三个,若每个人分六个,则最后一个学生最多得3个,求学生人数和苹果数,设有x个学生,依题意可列不等式组 .
15. 我们定义=ad-bc,例如=2×5-3×4=10-12=-2,则不等式组1<<3的解集是 .?
16. (1)解不等式组并把其解集在数轴上表示出来;
(2)解不等式组把解集在数轴上表示出来,并将解集中的整数解写出来.
17. 某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1 600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价-进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
18. 已知不等式组
(1)求此不等式组的整数解;
(2)若上述整数解满足方程mx+6=x-2m求m的值;
(3)在(2)的条件下,求m2 021-.
19. “全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1 520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2 000元,请求出所有符合条件的购书方案.
参 考 答 案
1. C
2. D
3. D
4. 解:(1) 因为解不等式①得x>0.5,解不等式②得x<2,所以不等式组的解集为0.5(2)解不等式-2x<6,得x>-3,解不等式3(x-2)≤x-4,得x≤1,将不等式解集表示在数轴上如图.
则不等式组的解集为-35. 44
6. 解:(1)①根据信息填表:
A地
B地
C地
合计
产品件数(件)
x
200-3x
2x
200
运费(元)
30x
1 600-24x
50x
56x+1 600
②由题意得 解得40≤x≤42. 因为x为整数,所以x=40或41或42,所以有三种方案,分别为:(ⅰ)A地40件,B地80件,C地80件;(ⅱ)A地41件,B地77件,C地82件;(ⅲ)A地42件,B地74件,C地84件.
(2)由题意得30x+8(n-3x)+50x=5 800,整理得n=725-7x. 因为n-3x≥0,所以x≤72.5. 又因为x≥0,所以0≤x≤72.5且x为整数. 因为n随x的增大而减小,所以当x=72时,n有最小值为221.
7. C
8. C
9. C
10. D
11. B
12. -7≤x<1
13. a≥1
14. 0≤(4x+3)-6(x-1)≤3
15.16. 解:(1)解不等式3x+1<2(x+2)得x<3;解不等式-x≤x+2,得x≥-1,所以原不等式组的解集是-1≤x<3. 在数轴上表示不等式组的解集为
(2)解不等式<1,得x<1;解不等式2(1-x)≤5,得x≥-,所以原不等式组的解集为-≤x<1,在数轴上表示不等式组的解集为
其整数解为-1,0.
17. 解:(1)设该超市购进甲商品x件,则购进乙商品(80-x)件,根据题意得10x+30(80-x)=1 600,解得x=40,80-x=40,则购进甲、乙两种商品各40件.
(2)设该超市购进甲商品x件,乙商品(80-x)件,由题意得 解得38≤x≤40,因为x为非负整数,所以x=38,39,40,相应地80-x=42,41,40,利润分别为5×38+10×42=190+420=610(元),5×39+10×41=195+410=605(元),5×40+10×40=200+400=600(元),则使该超市利润最大的方案是购进甲商品38件,乙商品42件.
18. 解:(1)解不等式①,得x<,解不等式②,得x>,所以原不等式组的解集为(2)把x=2代入方程mx+6=x-2m得2m+6=2-2m,解得m=-1.
(3)当m=-1时,m2 021-=(-1)2 021-=-1-1=-2.
19. 解:(1)设每本文学名著x元,动漫书y元,可得 解得 答:每本文学名著和动漫书各为40元和18元.
(2)设学校要求购买文学名著m本,则动漫书为(m+20)本,根据题意可得
解得26≤m≤,因为取整数,所以m取26,27,28;方案一:文学名著26本,动漫书46本;方案二:文学名著27本,动漫书47本;方案三:文学名著28本,动漫书48本.
第7章 一元一次不等式与不等式组
7.3 一元一次不等式组
要点测评 基础达标
要点1 一元一次不等式的实际应用
1. 下列各不等式组中,是一元一次不等式组的有( )
① ② ③ ④ ⑤2x-8<7-x<5.
A. ①②③ B. ②③⑤ C. ③④⑤ D. ①②③⑤
2. 如图表示下列四个不等式组中其中一个的解集,这个不等式组是( )
A. B. C. D.
要点2 一元一次不等式组的解法
3. 不等式组的解集在数轴上表示正确的是( )
A B
C D
4. (1)解不等式组:
(2)解不等式组:并把解集在数轴上表示出来.
要点3 一元一次不等式组的应用
5. 小华将若干个苹果放进若干个筐子里,若每个筐子放4个苹果,还剩20个苹果未放完;若每个筐子放8个苹果,则还有一个筐子没有放满,那么小华原来共有苹果 个.?
6. 温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,①根据信息填表:
A地
B地
C地
合计
产品件数(件)
x
2x
200
运费(元)
30x
②若运往B地的件数不多于运往C地的件数,总运费不超过4 000元,则有哪几种运输方案?
(2)若总运费为5 800元,求n的最小值.
课后集训 巩固提升
7. 不等式组的解集表示在数轴上正确的是( )
A B
C D
8. 不等式组的解集为x<2,则k的取值范围为( )
A. k>1 B. k<1 C. k≥1 D. k≤1
9. 不等式组的最大整数解是( )
A. 1 B. 2 C. 3 D. 4
10. 在x=-4,-1,0,3中,满足不等式组的x值是( )
A. -4和0 B. -4和-1 C. 0和3 D. -1和0
11. 关于x的不等式组的解集中至少有5个整数解,则正数a的最小值是( )
A. 3 B. 2 C. 1 D.
12. 不等式组的解集为 .?
13. 若关于x的一元一次不等式组无解,则a的取值范围是 .?
14. 把一篮苹果分给几个学生,若每个人分四个,则剩下三个,若每个人分六个,则最后一个学生最多得3个,求学生人数和苹果数,设有x个学生,依题意可列不等式组 .
15. 我们定义=ad-bc,例如=2×5-3×4=10-12=-2,则不等式组1<<3的解集是 .?
16. (1)解不等式组并把其解集在数轴上表示出来;
(2)解不等式组把解集在数轴上表示出来,并将解集中的整数解写出来.
17. 某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1 600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价-进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
18. 已知不等式组
(1)求此不等式组的整数解;
(2)若上述整数解满足方程mx+6=x-2m求m的值;
(3)在(2)的条件下,求m2 021-.
19. “全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1 520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2 000元,请求出所有符合条件的购书方案.
参 考 答 案
1. C
2. D
3. D
4. 解:(1) 因为解不等式①得x>0.5,解不等式②得x<2,所以不等式组的解集为0.5
则不等式组的解集为-3
6. 解:(1)①根据信息填表:
A地
B地
C地
合计
产品件数(件)
x
200-3x
2x
200
运费(元)
30x
1 600-24x
50x
56x+1 600
②由题意得 解得40≤x≤42. 因为x为整数,所以x=40或41或42,所以有三种方案,分别为:(ⅰ)A地40件,B地80件,C地80件;(ⅱ)A地41件,B地77件,C地82件;(ⅲ)A地42件,B地74件,C地84件.
(2)由题意得30x+8(n-3x)+50x=5 800,整理得n=725-7x. 因为n-3x≥0,所以x≤72.5. 又因为x≥0,所以0≤x≤72.5且x为整数. 因为n随x的增大而减小,所以当x=72时,n有最小值为221.
7. C
8. C
9. C
10. D
11. B
12. -7≤x<1
13. a≥1
14. 0≤(4x+3)-6(x-1)≤3
15.
(2)解不等式<1,得x<1;解不等式2(1-x)≤5,得x≥-,所以原不等式组的解集为-≤x<1,在数轴上表示不等式组的解集为
其整数解为-1,0.
17. 解:(1)设该超市购进甲商品x件,则购进乙商品(80-x)件,根据题意得10x+30(80-x)=1 600,解得x=40,80-x=40,则购进甲、乙两种商品各40件.
(2)设该超市购进甲商品x件,乙商品(80-x)件,由题意得 解得38≤x≤40,因为x为非负整数,所以x=38,39,40,相应地80-x=42,41,40,利润分别为5×38+10×42=190+420=610(元),5×39+10×41=195+410=605(元),5×40+10×40=200+400=600(元),则使该超市利润最大的方案是购进甲商品38件,乙商品42件.
18. 解:(1)解不等式①,得x<,解不等式②,得x>,所以原不等式组的解集为
(3)当m=-1时,m2 021-=(-1)2 021-=-1-1=-2.
19. 解:(1)设每本文学名著x元,动漫书y元,可得 解得 答:每本文学名著和动漫书各为40元和18元.
(2)设学校要求购买文学名著m本,则动漫书为(m+20)本,根据题意可得
解得26≤m≤,因为取整数,所以m取26,27,28;方案一:文学名著26本,动漫书46本;方案二:文学名著27本,动漫书47本;方案三:文学名著28本,动漫书48本.
