第六章平行四边形章末复习课件(23张PPT)
文档属性
| 名称 | 第六章平行四边形章末复习课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 856.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 15:08:32 | ||
图片预览








文档简介
课件23张PPT。章末复习北师大版 八年级下册一、知识结构1.两组对边分别平行的四边形是平行四边形.
2.平行四边形的性质(边,角,对角线,对称性)
(1)边的性质:平行四边形的对边相等;平行四边形的对边平行;
(2)角的性质:平行四边形的对角相等 ;(3)对角线的性质:平行四边形的对角线互相平分;
(4)平行四边形是中心对称图形 . 3.平行四边形的判定.
(1)两组对边分别平行的四边形是平行四边形(定义);
(2)两组对边分别相等的四边形是平行四边形 ;
(3) 对角线互相平分的四边形是平行四边形 ;
(4)一组对边平行且相等的四边形是平行四边形;
(5)两组对角分别相等的四边形是平行四边形 . 4.两条平行线间的距离的定义 .若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离,实际上平行线间的距离处处相等. 5.三角形的中位线 .
(1)三角形中位线的定义:连接三角线两边中点的线段叫做三角形的中位线 ;
(2)三角形中位线定理:三角形的中位线平行于三角线的第三边,且等于第三边的一半.
6.多边形的内角与外角和 .
(1)多边形:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形 ;
(2)n边形的内角和是(n-2)·180°;
(3)多边形的外角和等于360°. 1.在四边形ABCD中,若AB=CD,再添加一个条件为,就可以判定四边形ABCD为平行四边形.
答案:本题为开放式题目,只需添上一组能使四边形ABCD成平行四边形的条件即可,例AB∥CD.
2.已知E.F.G.H分别为?ABCD各边的中点,则四边形EFGH为.
答案:平行四边形. 3.下列结论正确的是( )
A.对角线相等且一组对角相等的四边形是平行四边形
B.一边长为5cm,两条对角线长分别是4cm和6cm的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
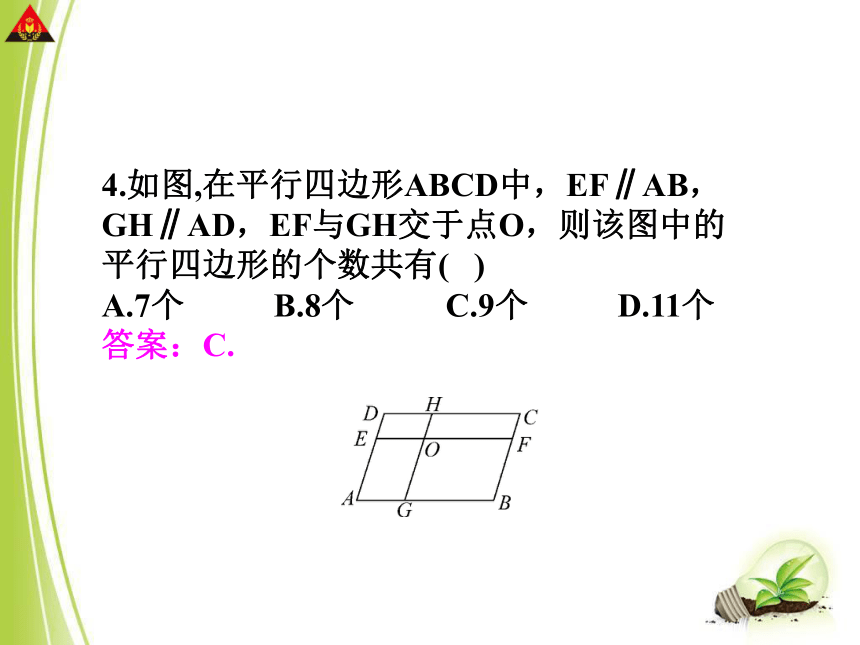
答案:C. 4.如图,在平行四边形ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
答案:C. 5.已知如图直线m∥n,A.B为直线n上两点,C.D为直线m上两点,BC与AD交于点O,则图中面积相等的三角形有()
A.1对 B.2对 C.3对 D.4对
答案:C. 6.若一个多边形内角和为1800°,求该多边形的边数.
解:设这个多边形的边数为n,则:
(n-2)×180°=1800°
n=12
即该多边形为十二边形 7.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作?ACED,延长DC交EB于F,求证:EF=FB.1.多边形的内角和与某一个外角的度数总和为1350°,求该多边形的边数.
分析:该外角的大小范围应该是0°<x<180°由此可得到该多边形内角和范围应该是1170°<1350°-x<1350°,而1350°-x=(n-2)·180° 解2:设该多边形边数为n,这个外角为x.
(n-2)·180°+x=1350°
0°<x<180°
∴1170°<1350°-x<1350°
∴1170°<(n-2)·180°<1350°
又∵n为整数,∴n=9.
则该多边形为九边形. 2.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
分析:(1)根据三角形中位线定理得GF∥EC, GF=12EC=EH,一组对边平行且相等的四边形是平行四边形,所以EGFH是平行四边形. 证明:(1)在△BEC中,∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=1/2EC .
又∵H是EC的中点,EH=1/2EC,
∴GF∥EH且GF=EH .
∴四边形EGFH是平行四边形. 3.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
解析:先证△EDB≌△CFE,可得BD=EF,ED=CF.∵BD=DA,CF=AF,∴ED=AF,EF=DA,∴四边形ADEF是平行四边形. 4.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.解:AE=CF.
理由:过E作EG∥CF交BC于G,∴∠3=∠C.∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.
∴∠C=∠BAD,∴∠3=∠BAD.
又∵∠1=∠2,BE=BE,
∴△ABE≌△GBE(AAS),∴AE=GE.
∵EF∥BC,EG∥CF,
∴四边形EGCF是平行四边形,
∴GE=CF,∴AE=CF. 通过本节课的复习,你取得了哪些经验? 1.从教材习题中选取;
2.完成练习册本课时的习题。青年是整个社会力量中的一部分最积极最有生气的力量。他们最肯学习,最少保守思想,在社会主义时代尤其是这样。 —— 毛泽东
2.平行四边形的性质(边,角,对角线,对称性)
(1)边的性质:平行四边形的对边相等;平行四边形的对边平行;
(2)角的性质:平行四边形的对角相等 ;(3)对角线的性质:平行四边形的对角线互相平分;
(4)平行四边形是中心对称图形 . 3.平行四边形的判定.
(1)两组对边分别平行的四边形是平行四边形(定义);
(2)两组对边分别相等的四边形是平行四边形 ;
(3) 对角线互相平分的四边形是平行四边形 ;
(4)一组对边平行且相等的四边形是平行四边形;
(5)两组对角分别相等的四边形是平行四边形 . 4.两条平行线间的距离的定义 .若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离,实际上平行线间的距离处处相等. 5.三角形的中位线 .
(1)三角形中位线的定义:连接三角线两边中点的线段叫做三角形的中位线 ;
(2)三角形中位线定理:三角形的中位线平行于三角线的第三边,且等于第三边的一半.
6.多边形的内角与外角和 .
(1)多边形:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形 ;
(2)n边形的内角和是(n-2)·180°;
(3)多边形的外角和等于360°. 1.在四边形ABCD中,若AB=CD,再添加一个条件为,就可以判定四边形ABCD为平行四边形.
答案:本题为开放式题目,只需添上一组能使四边形ABCD成平行四边形的条件即可,例AB∥CD.
2.已知E.F.G.H分别为?ABCD各边的中点,则四边形EFGH为.
答案:平行四边形. 3.下列结论正确的是( )
A.对角线相等且一组对角相等的四边形是平行四边形
B.一边长为5cm,两条对角线长分别是4cm和6cm的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
答案:C. 4.如图,在平行四边形ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
答案:C. 5.已知如图直线m∥n,A.B为直线n上两点,C.D为直线m上两点,BC与AD交于点O,则图中面积相等的三角形有()
A.1对 B.2对 C.3对 D.4对
答案:C. 6.若一个多边形内角和为1800°,求该多边形的边数.
解:设这个多边形的边数为n,则:
(n-2)×180°=1800°
n=12
即该多边形为十二边形 7.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作?ACED,延长DC交EB于F,求证:EF=FB.1.多边形的内角和与某一个外角的度数总和为1350°,求该多边形的边数.
分析:该外角的大小范围应该是0°<x<180°由此可得到该多边形内角和范围应该是1170°<1350°-x<1350°,而1350°-x=(n-2)·180° 解2:设该多边形边数为n,这个外角为x.
(n-2)·180°+x=1350°
0°<x<180°
∴1170°<1350°-x<1350°
∴1170°<(n-2)·180°<1350°
又∵n为整数,∴n=9.
则该多边形为九边形. 2.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
分析:(1)根据三角形中位线定理得GF∥EC, GF=12EC=EH,一组对边平行且相等的四边形是平行四边形,所以EGFH是平行四边形. 证明:(1)在△BEC中,∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=1/2EC .
又∵H是EC的中点,EH=1/2EC,
∴GF∥EH且GF=EH .
∴四边形EGFH是平行四边形. 3.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
解析:先证△EDB≌△CFE,可得BD=EF,ED=CF.∵BD=DA,CF=AF,∴ED=AF,EF=DA,∴四边形ADEF是平行四边形. 4.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.解:AE=CF.
理由:过E作EG∥CF交BC于G,∴∠3=∠C.∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.
∴∠C=∠BAD,∴∠3=∠BAD.
又∵∠1=∠2,BE=BE,
∴△ABE≌△GBE(AAS),∴AE=GE.
∵EF∥BC,EG∥CF,
∴四边形EGCF是平行四边形,
∴GE=CF,∴AE=CF. 通过本节课的复习,你取得了哪些经验? 1.从教材习题中选取;
2.完成练习册本课时的习题。青年是整个社会力量中的一部分最积极最有生气的力量。他们最肯学习,最少保守思想,在社会主义时代尤其是这样。 —— 毛泽东
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
