北师大版九年级数学下册2.2二次函数的图象与性质(1)教案
文档属性
| 名称 | 北师大版九年级数学下册2.2二次函数的图象与性质(1)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 10:05:17 | ||
图片预览


文档简介
二次函数的图象与性质(1)
一、教学目标
(一)知识与能力
1.会用描点法画y=ax函数的图象.
2.结合y=ax图象初步理解抛物线的开口方向,对称轴,顶点坐标,及y随x的变化情况.
3.为进一步理解其他形式二次函数打好基础.
(二)过程与方法
1.学生尝试去发现二次函数的图象特征.
2.在画图象过程中充分引导学生有目的去观察,体会其性质.
3.让学生去发现、归纳、概括.
(三)情感、态度与价值观
培养学生探索、观察、发现的良好品质以及克服困难的毅力,并学会归纳总结自己的结论,体会成功的喜悦,加强继续学习的兴趣.
二、教学重点、难点及教学突破
(一)教学重点
1.通过列表、描点、连线画函数y=ax图象.
2.通过图象初步理解二次函数性质.
(二)教学难点
结合图象理解抛物线开口方向、对称轴、顶点坐标及基本性质,并归纳总结出来.
(三)教学突破
有“一次函数”画图象的基础,在画图象的基本方法上学生问题不会太大,但教师应结合列表的数据引导学生对抛物线图象大致趋势的理解.学生在结合图象观察、体会性质时会有一些困难,教师应大胆让学生自己发现,归纳,鼓励学生讨论,交流.通过学生间相互的取长补短最终能突破重难点.
三、教学准备
(一)教师准备
教师准备标有平面直角坐标系的小黑板,作图工具.有条件应准备多媒体课件.
(二)学生准备
学生必备坐标纸,作图工具,草稿纸,同步练习册.
教学过程:
复习:y=ax2+bx+c (其中a、b、c是常数,a≠0)
当b=0时, y=ax2+c
当c=0时, y=ax2+bx
当b=0,c=0时, y=ax2
新课讲解:
数形结合,直观感受画二次函数y=x2的图象
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
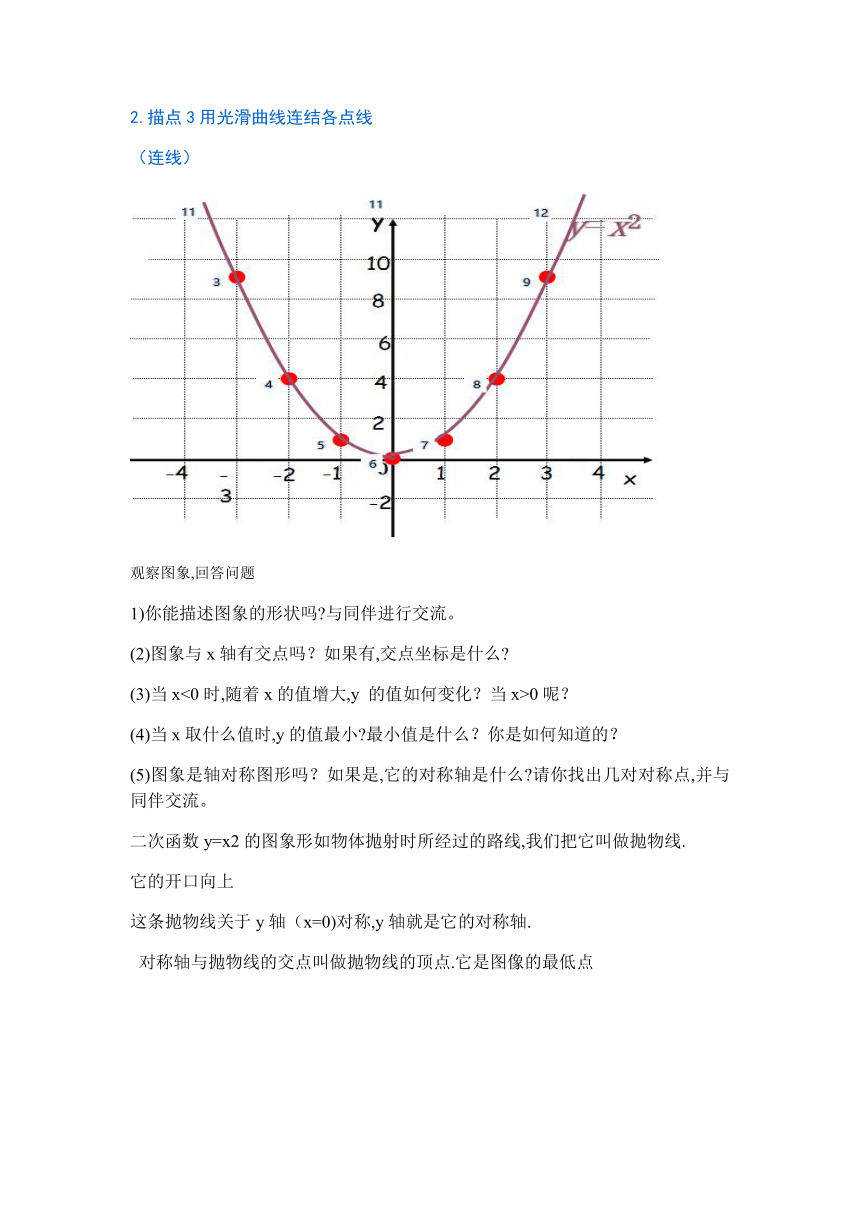
22.描点3用光滑曲线连结各点线
(连线)
观察图象,回答问题
1)你能描述图象的形状吗?与同伴进行交流。
(2)图象与x轴有交点吗?如果有,交点坐标是什么?
(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流。
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
它的开口向上
这条抛物线关于y轴(x=0)对称,y轴就是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.它是图像的最低点
做一做(1)二次函数y=-x2的图象是什么形状?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
你能根据表格中的数据作出猜想吗?
对比y=x2和y=-x2图象它们是不是轴对称
合作交流:二次函数y=ax2的图像和性质
练习1.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
解:(1)把(-2,-8)代入y=ax2,得 -8=a(-2)2,
解得a= -2,所求函数解析式为y= -2x2.
2)因为-4≠-2(-1)2 ,所以点B(-1 ,-4)不在此抛物线上.
3)由-6=-2x2 ,得x2=3, 所以纵坐标为-6的点有两个,它们分别是
2.填空:(1)抛物线y=x2的顶点坐标是(0,0),对称轴是y轴 ,在对称轴的右侧,y随着x的增大而增大;在对称轴的左侧,y随着x的增大而减小,当x=0 时,函数y的值最小,最小值是0 ,抛物线y=2x2在x轴的上方(除顶点外).
抛物线y=-x2在x轴的下方(除顶点外),在对称轴的左侧,y随着x的增大而增大 ;在对称轴的右侧,y随着x的增大而减小,当x=0时,函数y的值最大,最大值是0 ,当x≠0时,y<0.
本课小结
由二次函数y=x2和y=-x2知:
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大
作业布置:1.完成习题,做在书上,2.在下堂课之前备好坐标纸,作图工具,草稿纸,同步练习册.
