人教版八年级数学下册 17.1 勾股定理 同步练习含答案
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 同步练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 00:00:00 | ||
图片预览




文档简介
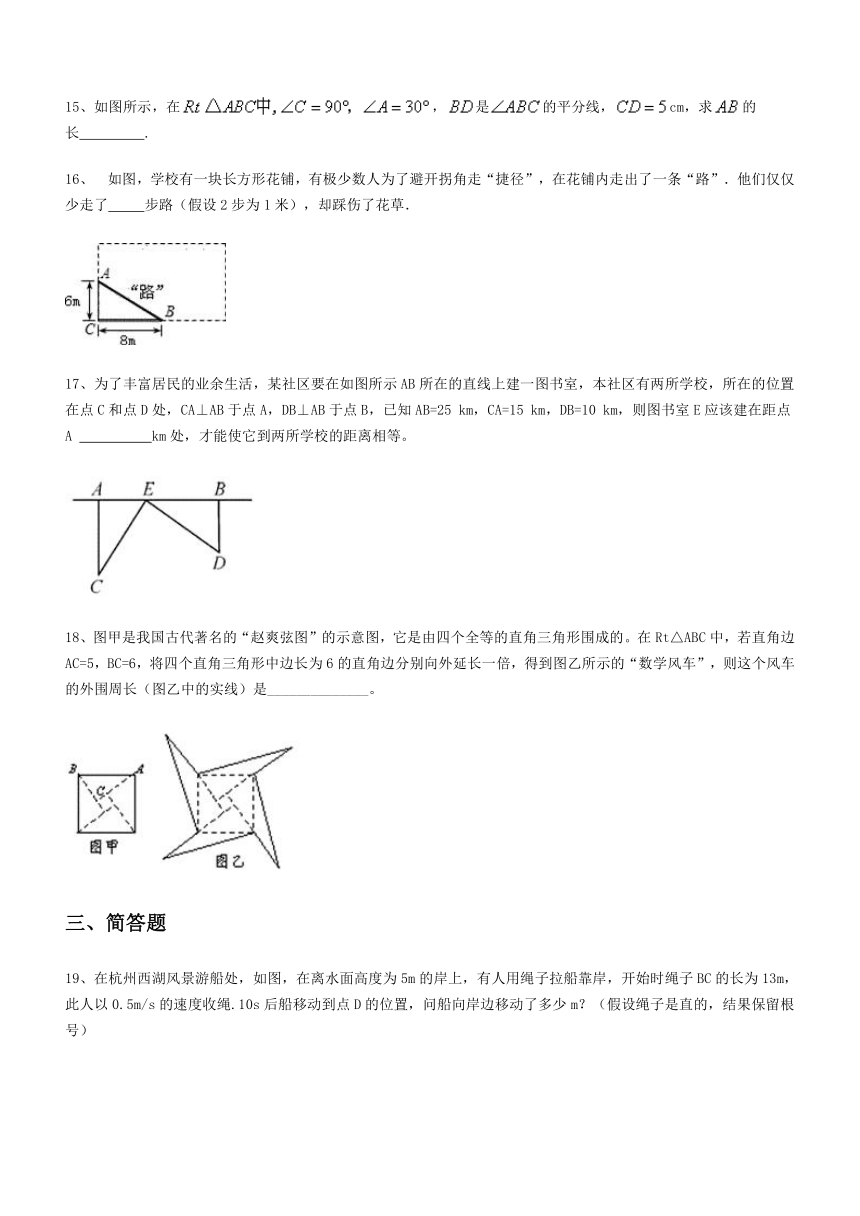
勾股定理 同步练习
1、选择题
1、在△ABC中,∠B=90°,若BC=3,AC=5,则AB等于( )
A.2?????? B.3?????? C.4??????? D.
2、如图,字母B所代表的正方形的面积是( )
A.12 cm2 B.15 cm2? C.144 cm2?? ?? D.306 cm2
3、我国是最早了解勾股定理的国家之一.下面四幅图中,不能证明勾股定理的是( )
A.????B.? C.???? D.
4、如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2?????? B.??????? C.???????? D.
5、如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
A.15尺 B.16尺?????? C.17尺?????? D.18尺
????? ??????????????
6、如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( )
A.3?????? B.3?????? C.6?????? D.6
7、如图,有一个由传感器控制的灯A装在门上方离地高4.5 m的墙上,任何东西只要移至距该灯5 m及5 m以内时,灯就会自动发光,请问一个身高1.5 m的学生要走到离墙多远的地方灯刚好发光?(??? )
A.4 m? B.3 m? C.5 m? D.7 m
8、如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行的最短路线的长是(???? )
A.(3+8)cm? ??? B.10 cm C.14 cm? ????? D.无法确定
9、如图,一辆小车沿坡度为的斜坡向上行驶13米,则小车上升的高度是( )
A.5米??????? B.6米???????? C.6.5米??????? D.12米
10、如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2m,则树高为(??? )米
A. ????B. ?????C. +1??? D. 3
11、有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了该图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是( )
A. 1???????B. 2015????????? C. 2016??????? D. 2017
12、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为13,则小正方形的面积为( )
A. 3???????? B. 4???????? C. 5???????? D. 6
二、填空题
13、若直角三角形的两小边为5、12,则第三边为 ?? .
14、.如图,写出字母所代表的正方形面积,SA= ?? ,SB ?? .
15、如图所示,在,是的平分线,cm,求的长 ?? .
16、?如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
17、为了丰富居民的业余生活,某社区要在如图所示AB所在的直线上建一图书室,本社区有两所学校,所在的位置在点C和点D处,CA⊥AB于点A,DB⊥AB于点B,已知AB=25 km,CA=15 km,DB=10 km,则图书室E应该建在距点A ?????km处,才能使它到两所学校的距离相等。
18、图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的。在Rt△ABC中,若直角边AC=5,BC=6,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是______________。
三、简答题
19、在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
20、如图,梯子AB斜靠在一竖直的墙上,梯子的底端A到墙根O的距离AO为2米,梯子的顶端B到地面的距离BO为6米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离A′O等于3米,同时梯子的顶端B下降至B′.求梯子顶端下滑的距离BB′.
21、如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮。两船同时起航,并同时到达折线A-B-C的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E点(? )。
A、在线段AB上? ??B、在线段BC上?? C、可以在线段AB上,也可以在线段BC上
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
22、《中华人民共和国道路交通安全法》规定:小汽车在城市街道上行驶的速度不得超过70km/h.如图,一辆小汽车在一条城市街道上直线行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪间的距离AB为50 m,则这辆小汽车超速了吗?说明理由.
23、问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图1中的直角三角形,写出勾股定理内容;
[尝试证明]
以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理.
24、如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=,BC=2,求证:△ABC是“美丽三角形”;
(2)在Rt△ABC中,∠C=90°,AC=2,若△ABC是“美丽三角形”,求BC的长.
参考答案
一、选择题
1、C;2、C;3、D;4、D;5、C;6、D;7、A;8、B;9、A;10、C;11、D;12、C????
二、填空题
13、 13
14、625??? 144
15、
16、8
17、10 km
18、76???
三、简答题
19、解:∵在Rt△ABC中,∠CAB=90°,BC=13m,AC=5m,
∴(m),
∵此人以0.5m/s的速度收绳,10s后船移动到点D的位置,
∴CD=13﹣0.5×10=8(m),
∴(m),
∴)(m).
答:船向岸边移动了)m.
20、解:在△RtAOB中,由勾股定理可知AB2=AO2+OB2=40,在Rt△A′OB′中由勾股定理可知A′B′2=A′O2+OB′2.
∵AB=A′B′,
∴A′O2+OB′2=40.
∴OB′==.
∴BB′=6﹣.
21、解:(1)B???????????????????????? ?
(2)设货轮从出发到两船相遇共航行了x海里,过D作DF⊥CB于F,连结DE,
则DE=,AB+BE=?????????
∵在等腰直角三角形ABC中,AB=BC=200,D是AC中点
∴DF=100,EF=300-??
在Rt△DEF中,,解得
∵>200,故DE=??????????
答:设货轮从出发到两船相遇共航行了海里。
22、超速
23、定理表述:
直角三角形中,两直角边的平方和等于斜边的平方.
证明:∵S四边形ABCD=S△ABE+S△AED+S△CDE,
=×2+,
又∵S四边形ABCD==,
∴=×2+,
∴(a+b)2=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
24、(1)证明:过点A作AD⊥BC于D,
∵AB=AC,AD⊥BC,
∴BD=BC=1,
由勾股定理得,AD==2,
∴AD=BC,即△ABC是“美丽三角形”;
(2)解:当AC边上的中线BD等于AC时,如图2,
BC==3,
当BC边上的中线AE等于BC时,
AC2=AE2﹣CE2,即BC2﹣(BC)2=(2)2,
解得,BC=4,
综上所述,BC=3或BC=4.
