6.2 利用万有引力定律解决综合问题 同步测试卷
文档属性
| 名称 | 6.2 利用万有引力定律解决综合问题 同步测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-10 00:00:00 | ||
图片预览




文档简介
专题二 利用万有引力定律解决综合问题
1.如图所示,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,下列说法正确的是( )
A.甲的向心加速度比乙的小
B.甲的运行周期比乙的小
C.甲的角速度比乙的大
D.甲的线速度比乙的大
2.一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为v。假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体重力,物体静止时,弹簧测力计的示数为N。已知引力常量为G,则这颗行星的质量为( )
A. B.
C. D.
3.地球的半径为R,地面上的重力加速度为g,在高空绕地球做匀速圆周运动的人造卫星,其最小周期是( )
A.π B.
C.π D.2π
4.(多选)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L。已知月球半径为R,万有引力常量为G。则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的质量m月=
C.月球的自转周期T=
D.月球的平均密度ρ=
5.已知引力常量G、月球中心到地球中心的距离R和月球绕地球运行的周期T,仅利用这三个数据,可以估算出的物理量有( )
A.月球的质量 B.地球的质量
C.地球的半径 D.地球的密度
6.一艘宇宙飞船绕一个不知名的行星表面飞行,要测定该行星的密度,仅仅需要( )
A.测定飞船的运行周期 B.测定飞船的环绕半径
C.测定行星的体积 D.测定飞船的运行速度
7.(多选)一些星球由于某种原因而发生收缩,假设该星球的直径缩小到原来的四分之一,若收缩时质量不变,则与收缩前相比(假设此时的引力仍适用万有引力定律)( )
A.同一物体在星球表面受到的重力增大到原来的4倍
B.同一物体在星球表面受到的重力增大到原来的16倍
C.星球的第一宇宙速度增大到原来的4倍
D.星球的第一宇宙速度增大到原来的2倍
8.因“光纤之父”高锟的杰出贡献,早在1996年中国科学院紫金山天文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。假设“高锟星”为均匀的球体,其质量为地球质量的倍,半径为地球半径的倍,则“高锟星”表面的重力加速度是地球表面的重力加速度的( )
A. B.
C. D.
9.如图所示,在火星与木星轨道之间有一小行星带,假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动。下列说法正确的是( )
A.太阳对各小行星的引力相同
B.各小行星绕太阳运动的周期均小于一年
C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值
D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值
10.如图所示,有甲、乙两颗卫星分别在不同的轨道围绕一个半径为R、表面重力加速度为g的行星运动。卫星甲、卫星乙各自所在的轨道平面相互垂直,卫星甲的轨道为圆,距离行星表面的高度为R,卫星乙的轨道为椭圆,M、N两点的连线为其椭圆轨道的长轴,且M、N两点间的距离为4R。则以下说法错误的是( )
A.卫星甲的线速度大小为
B.卫星乙运行的周期为4π
C.卫星乙沿椭圆轨道运行经过M点时的速度大于卫星甲沿圆轨道运行的速度
D.卫星乙沿椭圆轨道运行经过N点时的加速度小于卫星甲沿圆轨道运行的加速度
11.宇航员在某星球表面以初速度v0竖直向上抛出一个物体,物体上升的最大高度为h。已知该星球的半径为R,且物体只受该星球的引力作用。求:
(1)该星球表面的重力加速度;
(2)从这个星球上发射卫星的第一宇宙速度。
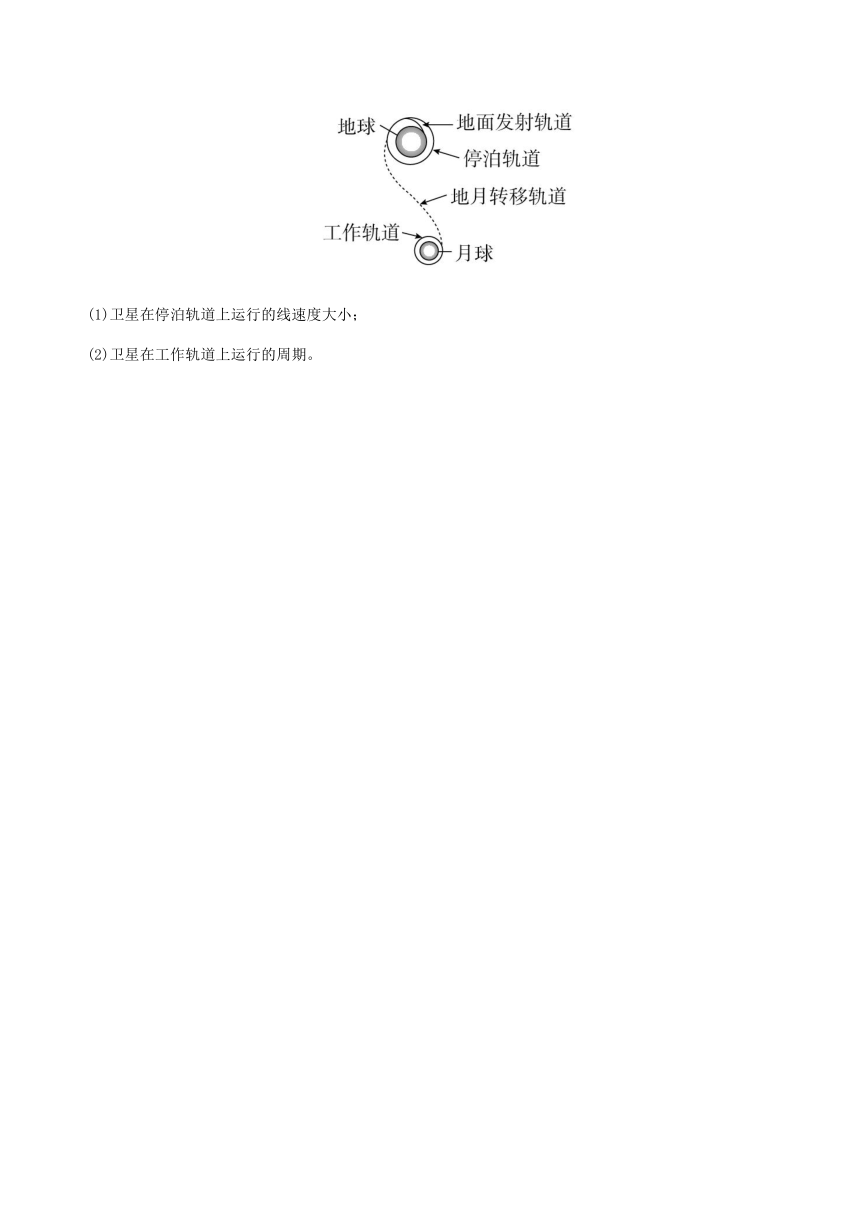
12.“嫦娥一号”探月卫星在空中的运动可简化为如图所示的过程,卫星由地面发射后,经过发射轨道进入停泊轨道,在停泊轨道经过调速后进入地月转移轨道,再次调速后进入工作轨道。已知卫星在停泊轨道和工作轨道运行的半径分别为R和R1,地球半径为r,月球半径为r1,地球表面重力加速度为g,月球表面重力加速度为。求:
(1)卫星在停泊轨道上运行的线速度大小;
(2)卫星在工作轨道上运行的周期。
答案
1.如图所示,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,下列说法正确的是( )
A.甲的向心加速度比乙的小
B.甲的运行周期比乙的小
C.甲的角速度比乙的大
D.甲的线速度比乙的大
答案 A
解析 甲、乙两卫星分别绕质量为M和2M的行星做匀速圆周运动,万有引力提供各自做匀速圆周运动所需的向心力。由牛顿第二定律G=man=mr=mω2r=m,可得an=,T=2π,ω=,v= 。由已知条件可得a甲<a乙,T甲>T乙,ω甲<ω乙,v甲<v乙,A正确,B、C、D错误。
2.一卫星绕某一行星表面附近做匀速圆周运动,其线速度大小为v。假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体重力,物体静止时,弹簧测力计的示数为N。已知引力常量为G,则这颗行星的质量为( )
A. B.
C. D.
答案 B
解析 设卫星的质量为m′,由万有引力提供向心力,得G=m′,m′=m′g。由质量为m的物体重力为N得g=,联立以上三式得M=,故B项正确。
3.地球的半径为R,地面上的重力加速度为g,在高空绕地球做匀速圆周运动的人造卫星,其最小周期是( )
A.π B.
C.π D.2π
答案 D
解析 由G=mr可得T=2π ,卫星的轨道半径越小,周期越小,当轨道半径等于地球半径时,周期最小,即Tmin=2π ,又GM=gR2,所以Tmin=2π ,故D正确。
4.(多选)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L。已知月球半径为R,万有引力常量为G。则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的质量m月=
C.月球的自转周期T=
D.月球的平均密度ρ=
答案 AB
解析 根据平抛运动规律,L=v0t,h=g月t2,联立解得g月=,A正确;由mg月=G,解得m月==,B正确;v0是小球做平抛运动的初速度,而非月球自转的线速度,C错误;月球的平均密度ρ==,D错误。
5.已知引力常量G、月球中心到地球中心的距离R和月球绕地球运行的周期T,仅利用这三个数据,可以估算出的物理量有( )
A.月球的质量 B.地球的质量
C.地球的半径 D.地球的密度
答案 B
解析 由天体运动规律知G=mR,可得地球质量M=,由于不知地球的半径,无法求地球的密度,故B正确。
6.一艘宇宙飞船绕一个不知名的行星表面飞行,要测定该行星的密度,仅仅需要( )
A.测定飞船的运行周期 B.测定飞船的环绕半径
C.测定行星的体积 D.测定飞船的运行速度
答案 A
解析 取飞船为研究对象,由G=mr及M=ρV=ρ·πr3,知ρ=,故选A。
7.(多选)一些星球由于某种原因而发生收缩,假设该星球的直径缩小到原来的四分之一,若收缩时质量不变,则与收缩前相比(假设此时的引力仍适用万有引力定律)( )
A.同一物体在星球表面受到的重力增大到原来的4倍
B.同一物体在星球表面受到的重力增大到原来的16倍
C.星球的第一宇宙速度增大到原来的4倍
D.星球的第一宇宙速度增大到原来的2倍
答案 BD
解析 在星球表面由重力近似等于万有引力mg=G可知,当星球半径减小为原来的时,同一物体在星球表面受到的重力增大为原来的16倍,A错误,B正确。由第一宇宙速度计算式v= 可知,星球的第一宇宙速度增大为原来的两倍,C错误,D正确。
8.因“光纤之父”高锟的杰出贡献,早在1996年中国科学院紫金山天文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。假设“高锟星”为均匀的球体,其质量为地球质量的倍,半径为地球半径的倍,则“高锟星”表面的重力加速度是地球表面的重力加速度的( )
A. B.
C. D.
答案 C
解析 根据黄金代换式g=,并利用题设条件,可求出==,C项正确。
9.如图所示,在火星与木星轨道之间有一小行星带,假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动。下列说法正确的是( )
A.太阳对各小行星的引力相同
B.各小行星绕太阳运动的周期均小于一年
C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值
D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值
答案 C
解析 根据万有引力定律F=G可知,由于各小行星的质量和到太阳的距离不同,万有引力不同,A项错误;由G=mr,得T=2π ,因为各小行星的轨道半径r大于地球的轨道半径,所以它们的运动周期均大于地球的公转周期,B项错误;向心加速度an==,内侧小行星到太阳的距离小,向心加速度大,C项正确;由G=m得线速度v= ,小行星的轨道半径大于地球的轨道半径,线速度小于地球绕太阳公转的线速度,D项错误。
10.如图所示,有甲、乙两颗卫星分别在不同的轨道围绕一个半径为R、表面重力加速度为g的行星运动。卫星甲、卫星乙各自所在的轨道平面相互垂直,卫星甲的轨道为圆,距离行星表面的高度为R,卫星乙的轨道为椭圆,M、N两点的连线为其椭圆轨道的长轴,且M、N两点间的距离为4R。则以下说法错误的是( )
A.卫星甲的线速度大小为
B.卫星乙运行的周期为4π
C.卫星乙沿椭圆轨道运行经过M点时的速度大于卫星甲沿圆轨道运行的速度
D.卫星乙沿椭圆轨道运行经过N点时的加速度小于卫星甲沿圆轨道运行的加速度
答案 A
解析 卫星甲绕中心天体做匀速圆周运动,由万有引力提供向心力得:G=m,其中r=2R,由行星表面万有引力等于重力得:G=mg,综上可计算出卫星甲环绕中心天体运动的线速度大小v= ,A项错误;同理可计算出卫星甲运行的周期T甲=4π ,由卫星乙椭圆轨道的半长轴等于卫星甲圆轨道的半径,根据开普勒第三定律可知,卫星乙运行的周期和卫星甲运行的周期相等,即T乙=T甲=4π,B项正确;卫星乙沿椭圆轨道经过M点时的速度大于在过M点的圆轨道上运行的卫星的线速度,而在过M点的圆轨道上运行的卫星的线速度大于卫星甲在圆轨道上的线速度,故卫星乙沿椭圆轨道运行经过M点的速度大于卫星甲的速度,C项正确;卫星运行时只受万有引力,向心加速度a=,与行星的距离r越大,a越小,D项正确。
11.宇航员在某星球表面以初速度v0竖直向上抛出一个物体,物体上升的最大高度为h。已知该星球的半径为R,且物体只受该星球的引力作用。求:
(1)该星球表面的重力加速度;
(2)从这个星球上发射卫星的第一宇宙速度。
答案 (1) (2)v0
解析 (1)设该星球表面的重力加速度为g,物体做竖直上抛运动,
由题意知v=2gh,得g=。
(2)卫星贴近星球表面运行,
则有mg=m,得v==v0。
12.“嫦娥一号”探月卫星在空中的运动可简化为如图所示的过程,卫星由地面发射后,经过发射轨道进入停泊轨道,在停泊轨道经过调速后进入地月转移轨道,再次调速后进入工作轨道。已知卫星在停泊轨道和工作轨道运行的半径分别为R和R1,地球半径为r,月球半径为r1,地球表面重力加速度为g,月球表面重力加速度为。求:
(1)卫星在停泊轨道上运行的线速度大小;
(2)卫星在工作轨道上运行的周期。
答案 (1)r (2)
解析 (1)设卫星在停泊轨道上运行的线速度为v,卫星质量为m,卫星做圆周运动的向心力由地球对它的万有引力提供,有G=m,且对在地球表面的质量为m′的物体有G=m′g,
由此得v=r。
(2)设卫星在工作轨道上运行的周期为T,
则有G=m2R1,
又对在月球表面的质量为m′的物体有
G=m′,
解得T=。
