人教版八年级数学下册17.1.1勾股定理 课件(共34张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1.1勾股定理 课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 19:53:30 | ||
图片预览





文档简介
(共34张PPT)
第十七章 勾股定理
Zx```xk
17.1 勾股定理
第1课时
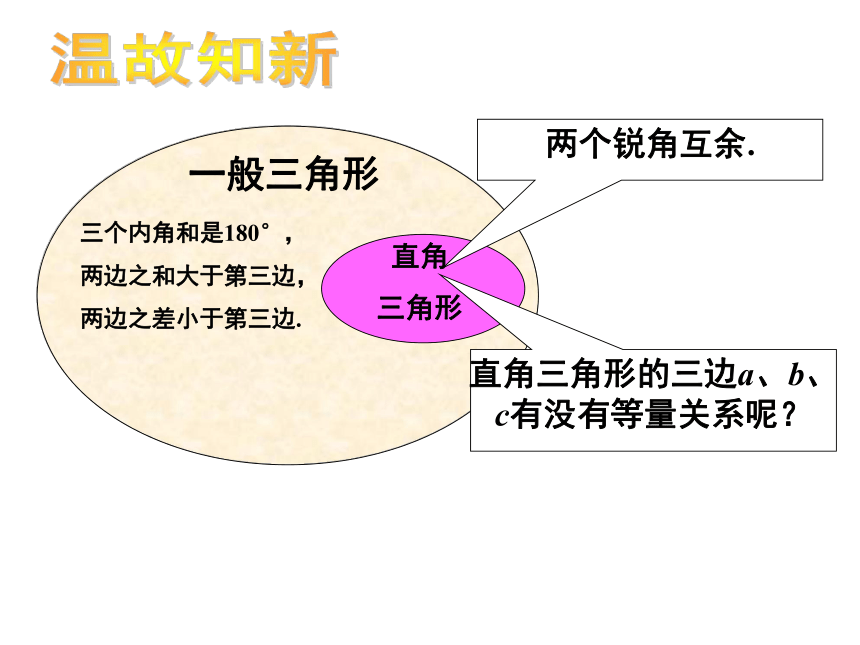
一般三角形
三个内角和是180°,
两边之和大于第三边,
两边之差小于第三边.
直角
三角形
两个锐角互余.
直角三角形的三边a、b、c有没有等量关系呢?
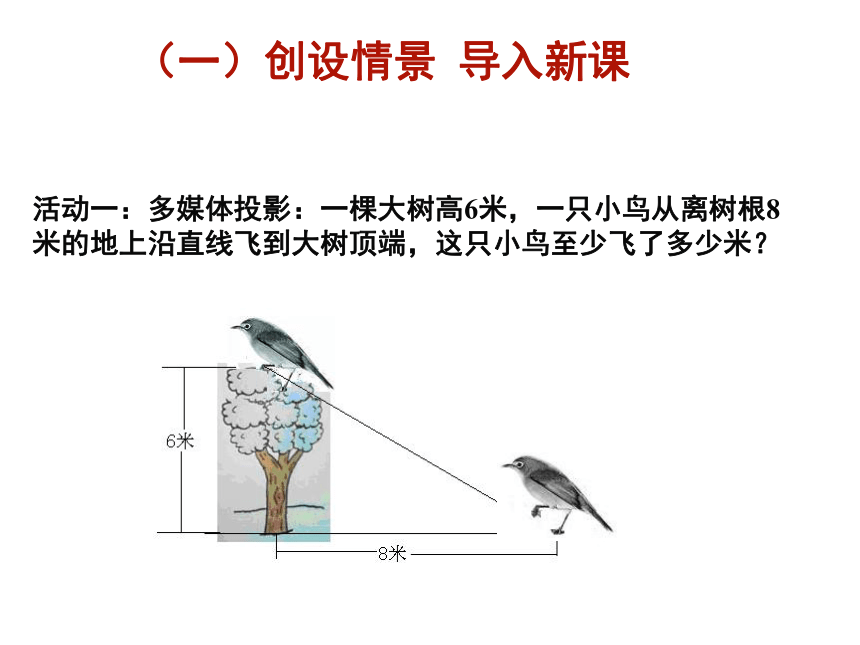
活动一:多媒体投影:一棵大树高6米,一只小鸟从离树根8米的地上沿直线飞到大树顶端,这只小鸟至少飞了多少米?
(一)创设情景 导入新课
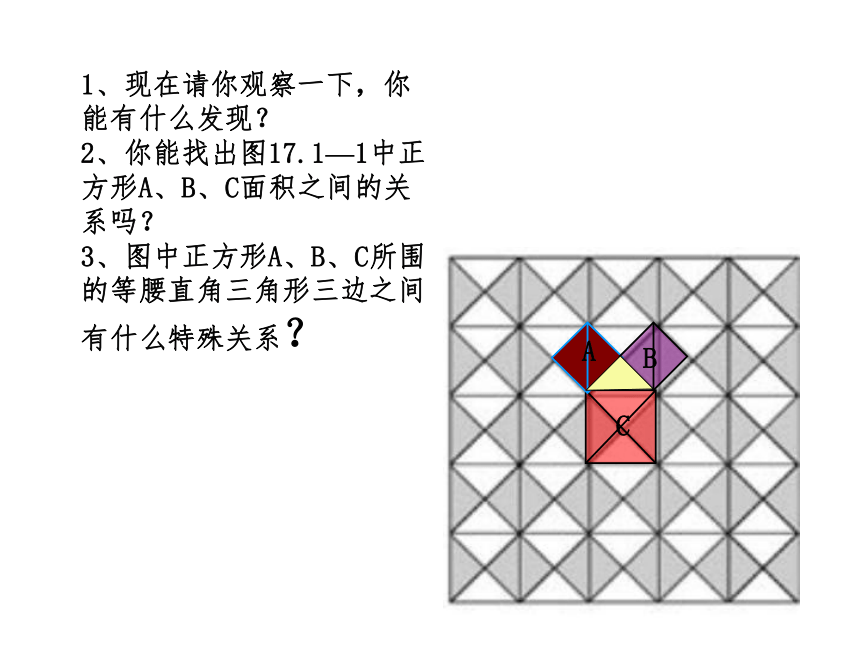
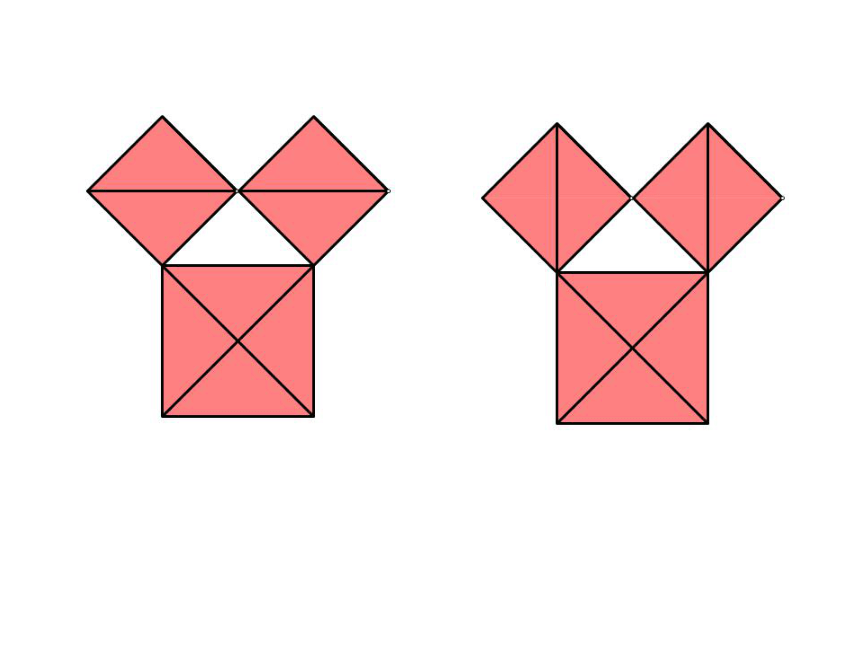
1、现在请你观察一下,你能有什么发现?
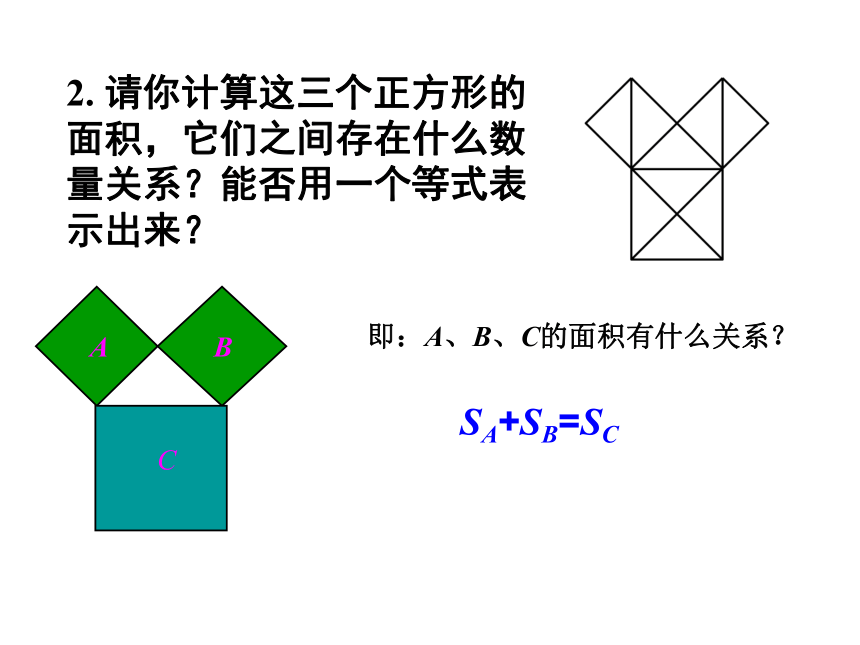
2、你能找出图17.1—1中正方形A、B、C面积之间的关系吗?
3、图中正方形A、B、C所围的等腰直角三角形三边之间有什么特殊关系?
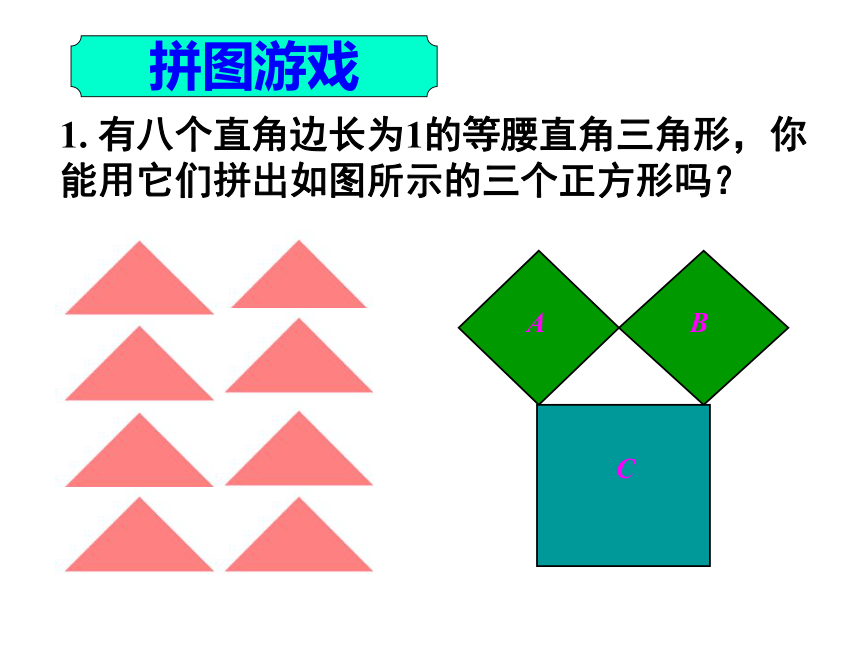
拼图游戏
1. 有八个直角边长为1的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗?
2. 请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?
即:A、B、C的面积有什么关系?
SA+SB=SC
3.由上面的条件可知,这三个正方形的边长分别是1、1和 ,那么刚才的面积关系可以用一个等量关系式来描述吗?请你写出这个等式.
两条直角边的平方和等于斜边的平方.
SA+SB=SC
+
=
(
)2
这里的等腰直角三角形如果腰长不是1,而是其他数,还会有刚才的结论吗? Z```x```xk
是不是所有的直角三角形
都是这样的呢?
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
4
16
?
?
9
9
A的面积 B的面积 C的面积
左图
右图
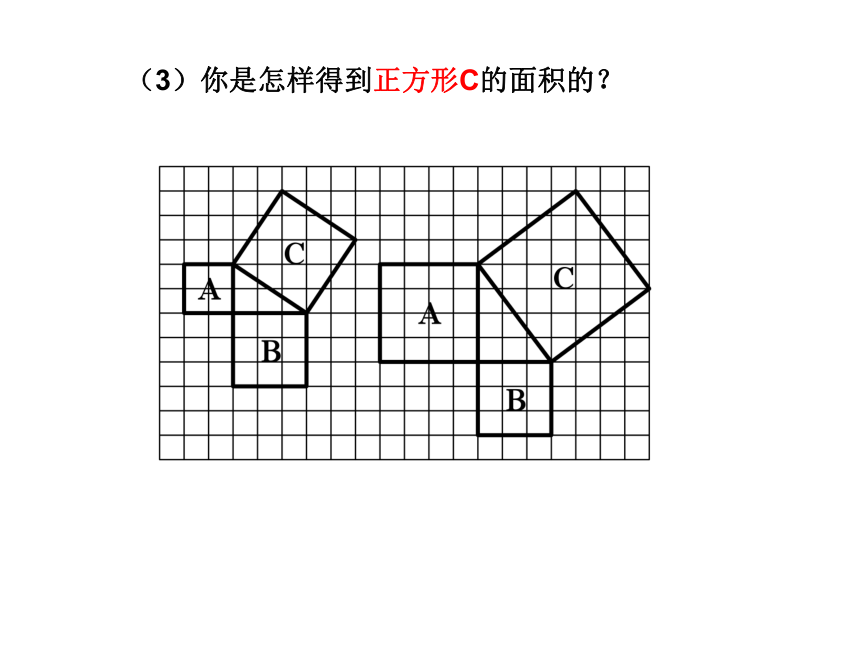
(3)你是怎样得到正方形C的面积的?
7
3
4
“补”的方法
SC = S大正方形 - 4×S小直角三角形
=
7
×
7
-
×
4
×
3
=
25
4
×
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
=
4
×
×
3
×
4
+
1
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
4 9
16 9
13
25
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
13
25
根据表中数据,你得到了什么?
+
=
A的面积 B的面积 C的面积
左图
右图
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
+
=
+
=
直角三角形的两条直角边的平方和等于斜边的平方.
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
+
=
b
a
a
b
c
c
a
a2+b2=c2
图2
自主证明
大正方形的面积=
小正方形的面积=
(b-a)2
·a·b·4+(b-a)2=
即:
+
=
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
自主证明
图1
图3
解:
解:
大正方形的面积=(b+a)2
小正方形的面积=
即(b+a)2=c2
+
4
×
·
ab
如果直角三角形两直角边分别为a、b,
斜边为c,那么
即 直角三角形两直角边的平方和
等于斜边的平方.
表示为:Rt△ABC中,∠C=90°,
定理:
+
=
+
=
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾股定理的由来
这个定理在中国又称为“商高定理”,商高是公元前十一世纪的中国人.当时中国的朝代是西周,
是奴隶社会时期.在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话.商高说:“…故折矩,勾广三,股修四,
经隅五.”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5.以后人们就简单地把这个
事实说成“勾三股四弦五”.由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
做“商高定理”.
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
(注意:哪条边是斜边)
+
=
=
-
活动五
1、求下图中字母A、B所代表的正方形的面积
81
B
625
400
(三)应用迁移,巩固提高
比一比看看谁算得快!
2、求出下图中直角三角形中未知边的长度
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 教材第24页练习第2题.
(三)应用迁移,巩固提高
本节课开始时的问题你能解决了吗?
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
1. 请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
第十七章 勾股定理
Zx```xk
17.1 勾股定理
第1课时
一般三角形
三个内角和是180°,
两边之和大于第三边,
两边之差小于第三边.
直角
三角形
两个锐角互余.
直角三角形的三边a、b、c有没有等量关系呢?
活动一:多媒体投影:一棵大树高6米,一只小鸟从离树根8米的地上沿直线飞到大树顶端,这只小鸟至少飞了多少米?
(一)创设情景 导入新课
1、现在请你观察一下,你能有什么发现?
2、你能找出图17.1—1中正方形A、B、C面积之间的关系吗?
3、图中正方形A、B、C所围的等腰直角三角形三边之间有什么特殊关系?
拼图游戏
1. 有八个直角边长为1的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗?
2. 请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?
即:A、B、C的面积有什么关系?
SA+SB=SC
3.由上面的条件可知,这三个正方形的边长分别是1、1和 ,那么刚才的面积关系可以用一个等量关系式来描述吗?请你写出这个等式.
两条直角边的平方和等于斜边的平方.
SA+SB=SC
+
=
(
)2
这里的等腰直角三角形如果腰长不是1,而是其他数,还会有刚才的结论吗? Z```x```xk
是不是所有的直角三角形
都是这样的呢?
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
4
16
?
?
9
9
A的面积 B的面积 C的面积
左图
右图
(3)你是怎样得到正方形C的面积的?
7
3
4
“补”的方法
SC = S大正方形 - 4×S小直角三角形
=
7
×
7
-
×
4
×
3
=
25
4
×
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
=
4
×
×
3
×
4
+
1
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
4 9
16 9
13
25
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
13
25
根据表中数据,你得到了什么?
+
=
A的面积 B的面积 C的面积
左图
右图
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
+
=
+
=
直角三角形的两条直角边的平方和等于斜边的平方.
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
+
=
b
a
a
b
c
c
a
a2+b2=c2
图2
自主证明
大正方形的面积=
小正方形的面积=
(b-a)2
·a·b·4+(b-a)2=
即:
+
=
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
自主证明
图1
图3
解:
解:
大正方形的面积=(b+a)2
小正方形的面积=
即(b+a)2=c2
+
4
×
·
ab
如果直角三角形两直角边分别为a、b,
斜边为c,那么
即 直角三角形两直角边的平方和
等于斜边的平方.
表示为:Rt△ABC中,∠C=90°,
定理:
+
=
+
=
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾股定理的由来
这个定理在中国又称为“商高定理”,商高是公元前十一世纪的中国人.当时中国的朝代是西周,
是奴隶社会时期.在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话.商高说:“…故折矩,勾广三,股修四,
经隅五.”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5.以后人们就简单地把这个
事实说成“勾三股四弦五”.由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
做“商高定理”.
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
(注意:哪条边是斜边)
+
=
=
-
活动五
1、求下图中字母A、B所代表的正方形的面积
81
B
625
400
(三)应用迁移,巩固提高
比一比看看谁算得快!
2、求出下图中直角三角形中未知边的长度
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 教材第24页练习第2题.
(三)应用迁移,巩固提高
本节课开始时的问题你能解决了吗?
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
1. 请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
