人教版数学八年级下册 19.2.2一次函数(3)(共30张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.2.2一次函数(3)(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 21:21:38 | ||
图片预览






文档简介
课件30张PPT。第十九章 一次函数19.2.2 一次函数(3)待定系数法
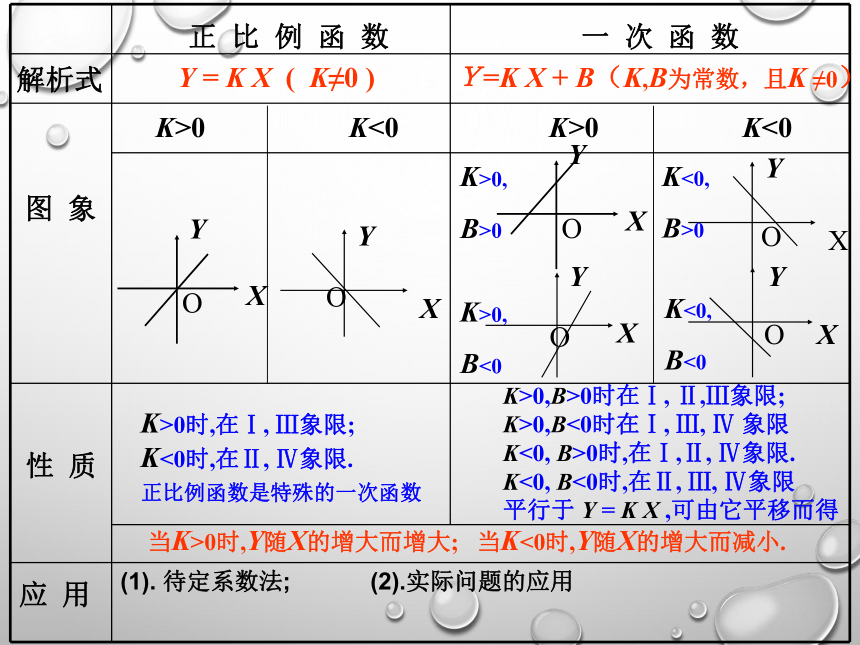
求一次函数解析式 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,
b>0k>0,
b<0k<0,
b>0k<0,
b<0yxoxyok>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.1、在函数y=2x中,函数y随自变量x的增大 .
2、已知一次函数y=kx+5过点P(-1,2),则k= .
3、已知一次函数y=2x+4的图像经过点(m,8),则m= .
4、一次函数y=-2x+1的图象经过第 象限,y随着x的增大而 ; y=2x -1图象经过第 象限,y随着x的增大而 .
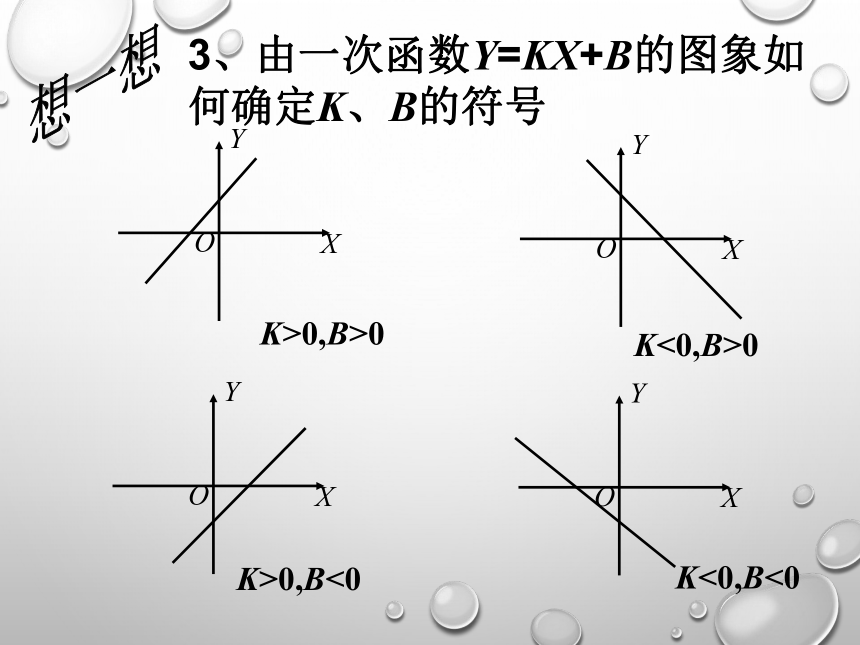
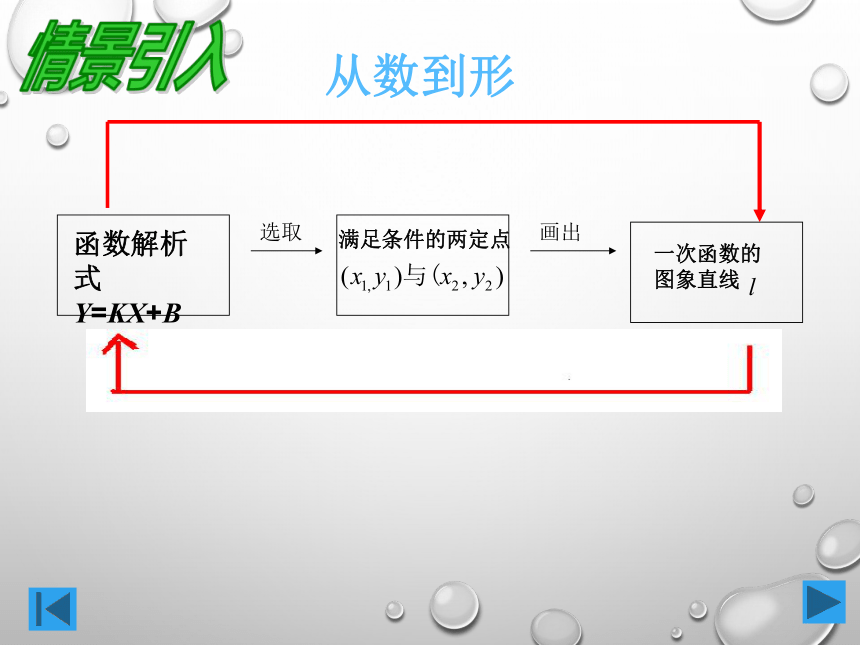
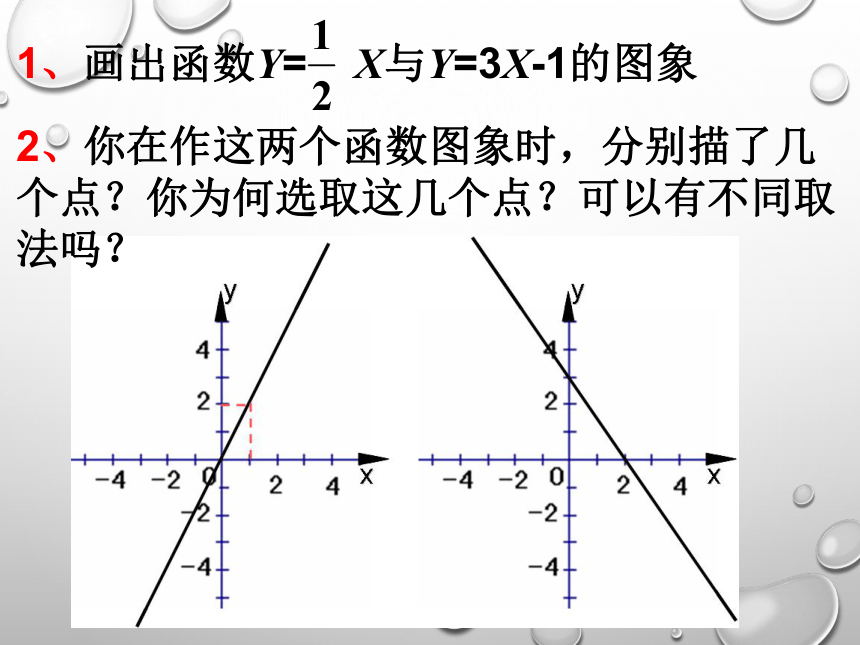
5、若一次函数y=x+b的图象过点A(1,-1),则b=________. y=kx+b温故知新1、复习:2、反思:画出 和 的图象你在作这两个函数图象时,分别描了几个点? 创设情境 提出问题可以有不同取法吗?k>0,b>0k>0,b<0k<0,b<0k<0,b>03、由一次函数y=kx+b的图象如何确定k、b的符号想一想函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取从数到形情景引入1.利用图像求函数的解析式 2.分析与思考
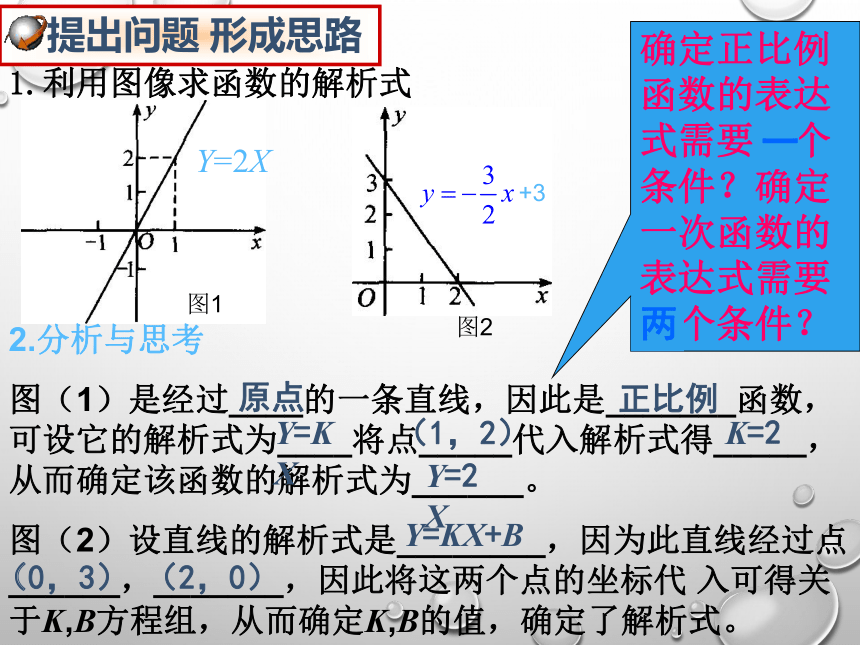
图(1)是经过____的一条直线,因此是_______函数,可设它的解析式为____将点_____代入解析式得_____,从而确定该函数的解析式为______。
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了解析式。(1,2)y=2xk=2y=kxy=kx+b(0,3)(2,0)正比例原点确定正比例函数的表达式需要几个
条件?确定一次函数的表达式需要几个条件?一两y=2x1、画出函数y= x与y=3x-1的图象2、你在作这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?例题:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.你能归纳出待定系数法求函数解析式的基本步骤吗?解:设这个一次函数的解析式为y=kx+b。
因为y=kx+b的图象过点(3,5)与(-4,-9),
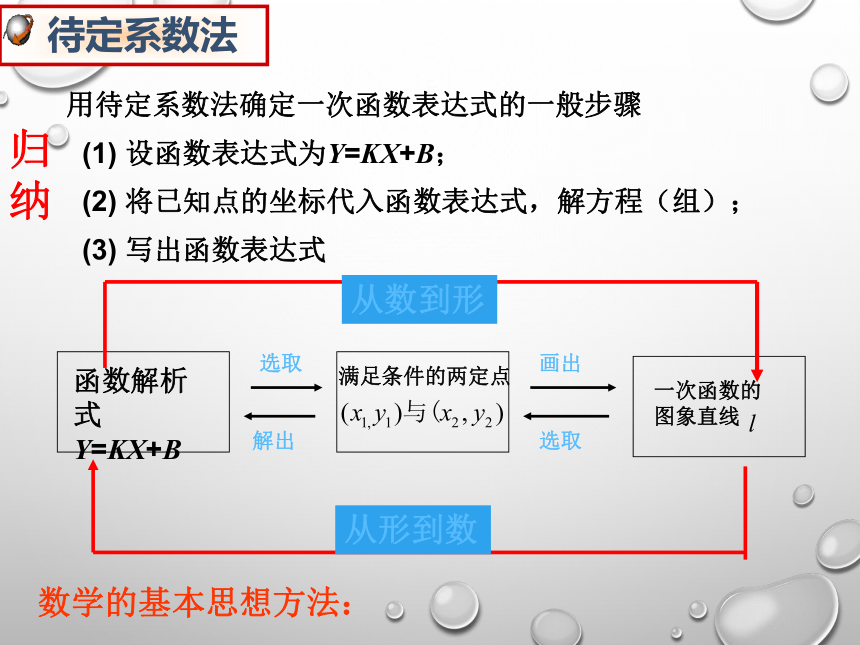
所以解得这个一次函数的解析式为y=2x-1.用待定系数法确定一次函数表达式的一般步骤
(1) 设函数表达式为y=kx+b;
(2) 将已知点的坐标代入函数表达式,解方程(组);
(3) 写出函数表达式归
纳函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法: 已知一次函数y=kx+b的图象如图所示,求函数表达式.
[分析] 从图象上可以看出,它与x轴交于点(-1,0),与y轴交于点(0,-3),代入关系式中,求出k为即可.∴∴此函数的表达式为y=-3x-3.解:由图象可知,图象经过点(-1,0)和(0,-3)两点,代入到y=kx+b中,得拓展举例 在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少?解:设购买量y与单价x的函数解析式为y=kx+b∵当x=1000时 y = 800;当x=2000时y = 700∴ x = 5000答:当一客户购买400kg,单价是5000元. 判断三点A(3,1),B(0,-2),C(4,2)是否在 同一条直线上.∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上. [分析] 由于两点确定一条直线,故选取其中两点,求经过
这两点的函数表达式,再把第三个点的坐标代入表达式中,若成立,说明在此直线上;若不成立,说明不在此直线上.1、写出两个一次函数,使它们的图象都经过点(-2,3).
2、生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6cm时,蛇长为45.5cm;当尾长为14cm时,蛇长为105.5cm,当一条蛇的尾长为10cm时,这条蛇的长度是多少?
3、一个一次函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,-6),求这个函数的解析式. 4、小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?已知一条直线与x轴交点的横坐
标为-1,与y轴交点的纵坐标为
-3,求这条直线的解析式.1.利用点的坐标求函数解析式小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。2.利用表格信息确定函数解析式3.根据实际情况收集信息求函数解析式在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧,当不挂物体时,弹簧长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。想一想确定正比例函数的解析式y=kx,需求哪个值?需要几个条件?总结:在确定函数解析式时,要求几个系数就需要知道几个条件。k的值确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件?一个条件k、b的值两个条件求函数解关系的一般步骤是怎样的呢?可归纳为:“一设、二列、三解、四还原”一设:设出函数关系式的一般形式y=kx+b;二列:根据已知两点的坐标列出关于k、b的二元
一次方程组;三解:解这个方程组,求出k、b的值;四还原:把求得的k、b的值代入y=kx+b,写出函
数关系式.求一次函数关系式常见题型:
1.利用图像求函数关系式
2.利用点的坐标求函数关系式
3.利用表格信息确定函数关系式
4.根据实际情况收集信息求函数关系式
1、已知直线y=kx+b,经过点A(0,6),B(1,4)
(1)写出表示这条直线的函数解析式。
(2)如果这条直线经过点P(m,2), 求m的值。
(3)求这条直线与x 轴,y 轴所围成的图形的面积。课堂练习2、已知直线y=kx+b在y轴上的截距为-2,且过点(-2,3)。
(1)求函数y的解析式;
(2)求直线与x轴交点坐标;
(3)x取何值时,y>0;
(4)判断点(2,-7)是否在此直线上。课堂练习1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 . 2、如图,是 函数图象,
它的解析式是 。-2y=-2x024yx正比例小试身手03-1xy3、直线y=kx+b在坐标系中的位置如图,则图像与x轴交点坐标为 ,与y轴交点坐标为 ,图像与坐标轴围成的三角形面积= 。4、已知y与x成正比例,并且函数的图象经过点(3,4)。
(1)求函数的解析式。
(2)求当x=6时y的值。4、你能在图象中找出满足函数的两点吗?064yx067yx-3 点(0,6)点(-3,4)点(7,0)点(0,6)若能,那就把它代到解析式 里可得y = kx+by = kx+by = kx+b某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。学以致用6050300x/kmy/升解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以①②解得1、正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5
(1)求△OAB的面积
(2)求这两个函数的解析式拓展延伸2、在平面直角坐标系内,一次函数y=kx+b
(kb>0,b<0)的图象分别与x轴、y轴和直线 x=4 交于点A、B、C,直线 x=4 与X轴交于点D,四边形OBCD
(O是坐标系原点)的面
积为10,若A点的横坐标
为 ,求这个一次函
数的解析式。4拓展延伸 小 结 应用线 基本知识基本问题一次函数的概念、图象、性质三个关系 : (1)概念与 k, b
(2)图象与 k, b
(3)面积与交点坐标应用知识线方法线图象与现实生活的联系
求一次函数解析式 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,
b>0k>0,
b<0k<0,
b>0k<0,
b<0yxoxyok>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.1、在函数y=2x中,函数y随自变量x的增大 .
2、已知一次函数y=kx+5过点P(-1,2),则k= .
3、已知一次函数y=2x+4的图像经过点(m,8),则m= .
4、一次函数y=-2x+1的图象经过第 象限,y随着x的增大而 ; y=2x -1图象经过第 象限,y随着x的增大而 .
5、若一次函数y=x+b的图象过点A(1,-1),则b=________. y=kx+b温故知新1、复习:2、反思:画出 和 的图象你在作这两个函数图象时,分别描了几个点? 创设情境 提出问题可以有不同取法吗?k>0,b>0k>0,b<0k<0,b<0k<0,b>03、由一次函数y=kx+b的图象如何确定k、b的符号想一想函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取从数到形情景引入1.利用图像求函数的解析式 2.分析与思考
图(1)是经过____的一条直线,因此是_______函数,可设它的解析式为____将点_____代入解析式得_____,从而确定该函数的解析式为______。
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了解析式。(1,2)y=2xk=2y=kxy=kx+b(0,3)(2,0)正比例原点确定正比例函数的表达式需要几个
条件?确定一次函数的表达式需要几个条件?一两y=2x1、画出函数y= x与y=3x-1的图象2、你在作这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?例题:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.你能归纳出待定系数法求函数解析式的基本步骤吗?解:设这个一次函数的解析式为y=kx+b。
因为y=kx+b的图象过点(3,5)与(-4,-9),
所以解得这个一次函数的解析式为y=2x-1.用待定系数法确定一次函数表达式的一般步骤
(1) 设函数表达式为y=kx+b;
(2) 将已知点的坐标代入函数表达式,解方程(组);
(3) 写出函数表达式归
纳函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法: 已知一次函数y=kx+b的图象如图所示,求函数表达式.
[分析] 从图象上可以看出,它与x轴交于点(-1,0),与y轴交于点(0,-3),代入关系式中,求出k为即可.∴∴此函数的表达式为y=-3x-3.解:由图象可知,图象经过点(-1,0)和(0,-3)两点,代入到y=kx+b中,得拓展举例 在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少?解:设购买量y与单价x的函数解析式为y=kx+b∵当x=1000时 y = 800;当x=2000时y = 700∴ x = 5000答:当一客户购买400kg,单价是5000元. 判断三点A(3,1),B(0,-2),C(4,2)是否在 同一条直线上.∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上. [分析] 由于两点确定一条直线,故选取其中两点,求经过
这两点的函数表达式,再把第三个点的坐标代入表达式中,若成立,说明在此直线上;若不成立,说明不在此直线上.1、写出两个一次函数,使它们的图象都经过点(-2,3).
2、生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6cm时,蛇长为45.5cm;当尾长为14cm时,蛇长为105.5cm,当一条蛇的尾长为10cm时,这条蛇的长度是多少?
3、一个一次函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,-6),求这个函数的解析式. 4、小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?已知一条直线与x轴交点的横坐
标为-1,与y轴交点的纵坐标为
-3,求这条直线的解析式.1.利用点的坐标求函数解析式小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。2.利用表格信息确定函数解析式3.根据实际情况收集信息求函数解析式在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧,当不挂物体时,弹簧长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。想一想确定正比例函数的解析式y=kx,需求哪个值?需要几个条件?总结:在确定函数解析式时,要求几个系数就需要知道几个条件。k的值确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件?一个条件k、b的值两个条件求函数解关系的一般步骤是怎样的呢?可归纳为:“一设、二列、三解、四还原”一设:设出函数关系式的一般形式y=kx+b;二列:根据已知两点的坐标列出关于k、b的二元
一次方程组;三解:解这个方程组,求出k、b的值;四还原:把求得的k、b的值代入y=kx+b,写出函
数关系式.求一次函数关系式常见题型:
1.利用图像求函数关系式
2.利用点的坐标求函数关系式
3.利用表格信息确定函数关系式
4.根据实际情况收集信息求函数关系式
1、已知直线y=kx+b,经过点A(0,6),B(1,4)
(1)写出表示这条直线的函数解析式。
(2)如果这条直线经过点P(m,2), 求m的值。
(3)求这条直线与x 轴,y 轴所围成的图形的面积。课堂练习2、已知直线y=kx+b在y轴上的截距为-2,且过点(-2,3)。
(1)求函数y的解析式;
(2)求直线与x轴交点坐标;
(3)x取何值时,y>0;
(4)判断点(2,-7)是否在此直线上。课堂练习1、正比例函数 y=kx 的图象过点(-1,2),
则 k= , 该函数解析式为 . 2、如图,是 函数图象,
它的解析式是 。-2y=-2x024yx正比例小试身手03-1xy3、直线y=kx+b在坐标系中的位置如图,则图像与x轴交点坐标为 ,与y轴交点坐标为 ,图像与坐标轴围成的三角形面积= 。4、已知y与x成正比例,并且函数的图象经过点(3,4)。
(1)求函数的解析式。
(2)求当x=6时y的值。4、你能在图象中找出满足函数的两点吗?064yx067yx-3 点(0,6)点(-3,4)点(7,0)点(0,6)若能,那就把它代到解析式 里可得y = kx+by = kx+by = kx+b某车油箱现有汽油50升,行驶时,油箱中的余油量y(升)
是行驶路程x(km)的一次函数,其图象如图所示
求y与x的函数关系式,并写出自变量x的取值范围。学以致用6050300x/kmy/升解:设函数解析式为y = kx+b,且图象过
点(60,30)和点(0,50),所以①②解得1、正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5
(1)求△OAB的面积
(2)求这两个函数的解析式拓展延伸2、在平面直角坐标系内,一次函数y=kx+b
(kb>0,b<0)的图象分别与x轴、y轴和直线 x=4 交于点A、B、C,直线 x=4 与X轴交于点D,四边形OBCD
(O是坐标系原点)的面
积为10,若A点的横坐标
为 ,求这个一次函
数的解析式。4拓展延伸 小 结 应用线 基本知识基本问题一次函数的概念、图象、性质三个关系 : (1)概念与 k, b
(2)图象与 k, b
(3)面积与交点坐标应用知识线方法线图象与现实生活的联系
