湖南省邵阳市崀山培英学校2018-2019学年高二下学期期中考试数学试卷(word版)
文档属性
| 名称 | 湖南省邵阳市崀山培英学校2018-2019学年高二下学期期中考试数学试卷(word版) | 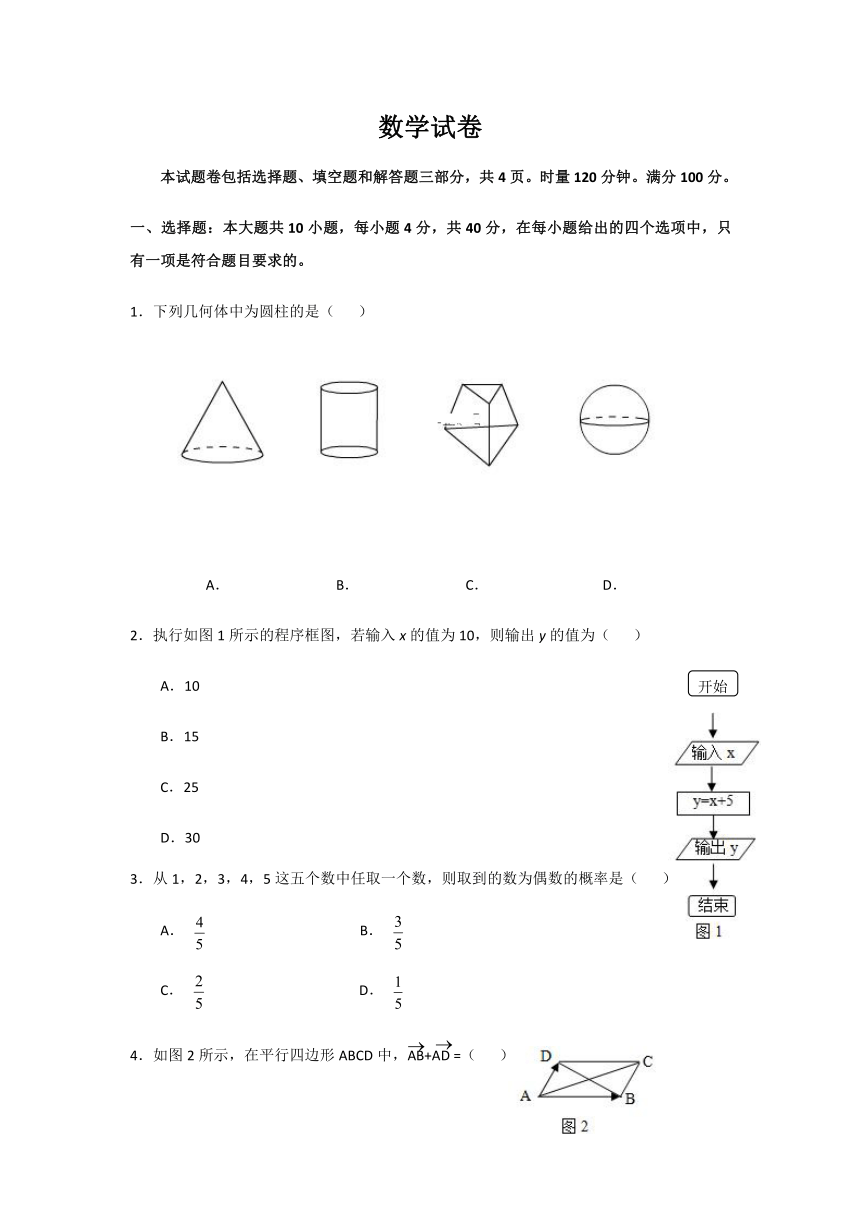 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-12 11:41:50 | ||
图片预览





文档简介
数学试卷
本试题卷包括选择题、填空题和解答题三部分,共4页。时量120分钟。满分100分。
一、选择题:本大题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列几何体中为圆柱的是( )
A. B. C. D.
2.执行如图1所示的程序框图,若输入x的值为10,则输出y的值为( )
A.10
B.15
C.25
D.30
3.从1,2,3,4,5这五个数中任取一个数,则取到的数为偶数的概率是( )
A. B.
C. D.
4.如图2所示,在平行四边形ABCD中,AB+AD =( )
A.AC B.CA
C.BD D.DB
5.已知函数y=f (x) (x [-1,5])的图像如图3所示,则f (x)的单调递减区间为( )
A.[-1,1]
B.[1,3]
C.[3,5]
D.[-1,5]
6.已知a>b,c>d,则下列不等式恒成立的是( )
A.a+c>b+d B. a+d>b+c
C.a-c>b-d D. a-b>c-d
7.为了得到函数的图像,只需将的图像向左平移( )
A.个单位长度 B.个单位长度
C.个单位长度 D.个单位长度
8.函数f (x)=log2(x-1)的零点为( )
A.4 B.3 C.2 D.1
9.在△ABC中,已知A=30°,B=45°,AC=,则BC=( )
A. B. C. D.1
10.过点M (2,1)作圆C:(x-1)2+y2=2的切线,则切线条数为( )
A.0 B.1 C.2 D.3
二、填空题:本大题共5小题,每小题4分,共20分。
11.直线y=x+3在y轴上的截距为
12.比较大小:sin25° sin23°(填“>”或“<")
13.已知集合A={1,2},B={,x}.若A∩B={2},则x=
14.某工厂甲、乙两个车间生产了同一种产品,数量分别为60件、40件,现用分层抽样方法抽取一个容量为n的样本进行质量检测,已知从甲车间抽取了6件产品,则n=
15.设x,y满足不等式组 ,则z=2x-y的最小值为
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分6分)
已知函数(x≠0)
(1)求f (1)的值;
(2)判断函数f (x)的奇偶性,并说明理由。
17,(本小题满分8分)
某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分,根据学生对食堂用餐满意度的评分,得到如图4所示的频率分布直方图。
(1)求频率分布直方图中a的值:
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂用餐
的3000名学生中“满意”的人数。
18.(本小题满分8分)
已知向量= (sinx,cosx),= ( , )
(1)若=,求tanx的值;
(2)设函数f (x)=·+2,求f (x)的值域。
19.(本小题满分8分)
如图5所示,四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD
(1)求证:CD⊥平面PAD;
(2)若E为PD的中点,三棱锥C-ADE的体积为,求四棱锥P-ABCD的侧面积。
20.(本小题满分10分)
在等差数列{an}中,已知a1=1,a2+a3=5.
(1)求an;
(2)设bn=an· ,求数列{bn}的前n项和Tn;
(3)对于(2)中的Tn,设,求数列{cn}中的最大项。
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C A B A D C D B
二、填空题
11.3 12.> 13.2 14. .10 15.
三、解答题
16.
解:(1)f(1)=2
(2)定义域为,
所以为奇函数。
17.解(1)由频率分布直方图的矩形面积和为1可知:
所以
(2)样本中不低于80分的频率为
由样本估计总体可得3000名学生中不低于80分的频率为约为,所以满意的人数为。故该校在校食堂用餐的3000名学生中“满意”的人数约为2100人。
18.解:(1)则
所以
(2)
因为,所以的值域为。
开始
C
