人教版数学七年级下册第5.2平行线及其判定学案(含答案)
文档属性
| 名称 | 人教版数学七年级下册第5.2平行线及其判定学案(含答案) | 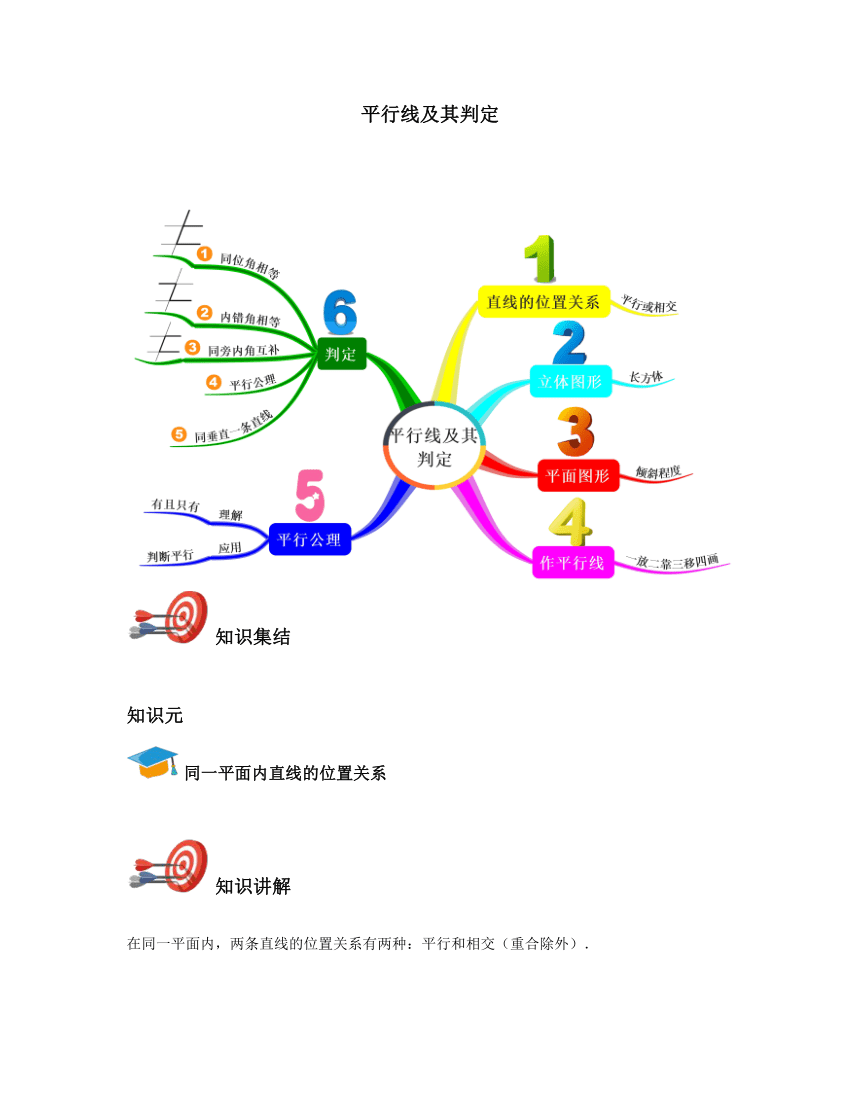 | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-10 22:50:41 | ||
图片预览




文档简介
平行线及其判定
知识集结
知识元
同一平面内直线的位置关系
知识讲解
在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外).
?
例题精讲
同一平面内直线的位置关系
例1.
下列叙述中,正确的是( ).
A.在同一平面内,两条直线的位置关系有三种,分别是相交、平行、垂直
B.不相交的两条直线叫平行线
C.两条直线的铁轨是平行的
D.我们知道,对顶角是相等的,那么反过来,相等的角就是对顶角
【答案】C
【解析】
题干解析:
解:A、在同一平面内,两条直线的位置关系有两种,分别是相交、平行,故A错误;
B、在同一个平面内,不相交的两条直线叫平行线,故B错误;
C、两条直线的铁轨是平行的,故C正确;
D、我们知道,对顶角是相等的,那么反过来,相等的角不一定是对顶角,故D错误;故选:C.
例2.
下列与垂直相交的说法:
①平面内,垂直于同一条直线的两条直线互相平行;
②平面内,一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;
③平面内,一条直线不可能与两条相交直线都垂直.
其中说法错误的个数有( ).
A.3个 B.2个 C.1个 D.0个
【答案】D
【解析】
题干解析:
解:由垂直的定义和平行线的判定方法可知:
①在同一平面内,垂直于同一条直线的两条直线互相平行;
②在同一平面内一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;
③在同一平面内,一条直线不可能与两条相交直线都垂直,这三种说法都正确.故选D.
立体图形中平行线的判断
知识讲解
在正方体长方体当中也会考察棱和边的位置关系,准备把握平行线定义是解题关键。
例题精讲
立体图形中平行线的判断
例1.
如图,在长方体ABCD﹣EFGH中,棱AB与棱HG的位置关系是 .
【答案】
平行
【解析】
题干解析:解:∵在长方体ABCD﹣EFGH中,HG∥EF,EF∥AB,∴AB∥HG,故答案为:平行.
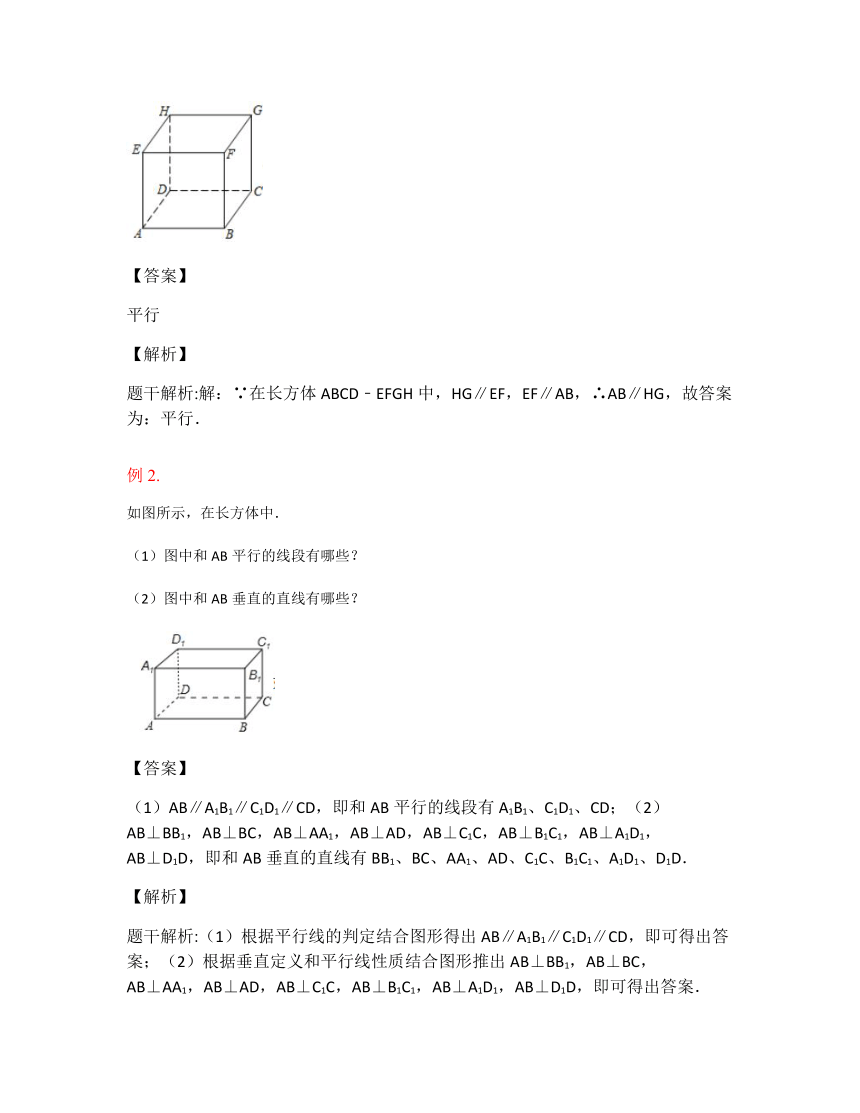
例2.
如图所示,在长方体中.
(1)图中和AB平行的线段有哪些?
(2)图中和AB垂直的直线有哪些?
【答案】
(1)AB∥A1B1∥C1D1∥CD,即和AB平行的线段有A1B1、C1D1、CD;(2)AB⊥BB1,AB⊥BC,AB⊥AA1,AB⊥AD,AB⊥C1C,AB⊥B1C1,AB⊥A1D1,AB⊥D1D,即和AB垂直的直线有BB1、BC、AA1、AD、C1C、B1C1、A1D1、D1D.
【解析】
题干解析:(1)根据平行线的判定结合图形得出AB∥A1B1∥C1D1∥CD,即可得出答案;(2)根据垂直定义和平行线性质结合图形推出AB⊥BB1,AB⊥BC,AB⊥AA1,AB⊥AD,AB⊥C1C,AB⊥B1C1,AB⊥A1D1,AB⊥D1D,即可得出答案.
平面图形中平行线判断
知识讲解
在同一个平面的直线,我们可以通过其倾斜程度来判断是否平行。
例题精讲
平面图形中平行线判断
例1.
如图,在同一平面内,有三条直线a、b、c,且a∥b,如果直线a与c交于点O,那么直线c与b的位置关系是 .
【答案】
相交
【解析】
题干解析:两直线平行,如果第三条直线与平行线中的一条相交,那么与另一条也相交.
例2.
右图的网格纸中,AB∥ ,AB⊥ .
【答案】
CD
AE
【解析】
题干解析:由图形不难得出AB∥CD,而CD又垂直AE,则可得AB与AE垂直.解:由图可得AB∥CD,而CD⊥AE,∴可得AB⊥AE.
作图-作平行线
知识讲解
平行线的画法:
一放:放三角板,把直角三角板的一条直角边与已知边重合
二靠:靠直尺,把直尺靠在直角三角板另一条直角边上
三移:直尺固定不动,移动三角尺使其边与直线外已知点重合
四画:沿着直角三角板直角边画直线
例题精讲
作图-作平行线
例1.
我们已经掌握“在同一平面内,垂直于同一条直线的两条直线互相平行”这一判定两直线平行的方法.如图,已知直线AB和直线外一点C,请按照上述方法利用三角尺过点C画AB的平行线.(保留作图痕迹,不用写作法).
【答案】
解:如图所示:EF为所求作的图形.
【解析】
题干解析:利用直角三角板过点C作CD⊥AB,再利用直角三角板过点C作EF⊥CD.
例2.
用三角尺、量角器或直尺画图,不要求写画法.
(1)过点P画OA的平行线,交射线OB于点M;
(2)过点P画OB的垂线,垂足为N;
(3)比较下列线段的长短:PM PN(用“>”、“=”或“<”填写).
【答案】
解:(1)如图所示:(2)如图所示:(3)根据垂线段最短可得PM>PN.
【解析】
题干解析:(1)利用平行线的画法过P画PM∥AO即可;(2)里用直角三角板,一条直角边与OB重合,沿BO移动三角板使另一条直角边过点P画直线即可;(3)根据垂线段最短可直接得到答案.
平行公理的理解
知识讲解
平行线公理及推论:
(1)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
?(2)平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思.
(3)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(4)平行公理的推论可以看做是平行线的一种判定方法,在解题中要注意该结论在证明直线平行时应用.
?
例题精讲
平行公理的理解
例1.
过一点画已知直线的平行线( ).
A.有且只有一条 B.不存在
C.有两条 D.不存在或有且只有一条
【答案】D
【解析】
题干解析:
解:若点在直线上,过这点不能画已知直线的平行线;
若点在直线外,根据平行公理,有且只有一条直线与已知直线平行.
故选D.
例2.
如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
【答案】
解:(1)如图,过直线a外的一点画直线a的平行线,有且只有一条直线与直线a平行(2)过点C画直线a的平行线,它与过点B的平行线平行.理由如下:如图,∵b∥a,c∥a,∴c∥b.
【解析】
题干解析:根据平行公理及推论进行解答.
平行公理推论应用
知识讲解
如果两条直线都和第三条直线平行,那么这两条直线平行,可以作为判定直线平行的依据。
例题精讲
平行公理推论应用
例1.
三条直线a、b、c,若a∥c,b∥c,则a与b的位置关系是( ).
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
【答案】B
【解析】
题干解析:
解:由于直线a、b都与直线c平行,依据平行公理的推论,可推出a∥b.故选B.
例2.
下列语句:
①不相交的两条直线叫平行线
②在同一平面内,两条直线的位置关系只有两种:相交和平行
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行,那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是( ).
A.1 B.2 C.3 D.4
【答案】B
【解析】
题干解析:
解:①不相交的两条直线叫平行线,必须是在同一平面内,故错误;
②在同一平面内,两条直线的位置关系只有两种:相交和平行,正确;
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行,错误;
④如果两条直线都和第三条直线平行,那么这两条直线平行,故正确;
⑤在同一平面内,过一点有且只有一条直线与已知直线平行,故错误;
故选:B.
例3.
如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DCC于Q点
(1)PQ与BC平行吗?为什么?
(2)测量DQ与CD的长,DQ与CQ是否相等?
【答案】
解:(1)PQ∥BC,理由如下:∵PQ∥AD又∵AD∥BC∴PQ∥BC(在同一平面内,平行于同一直线的两直线平行);(2)通过测量,可得出DQ=CQ,
【解析】
题干解析:(1)根据平行线的传递性可得出答案;(2)先测量。
同位角相等,两直线平行
知识讲解
定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
例题精讲
同位角相等,两直线平行
例1.
如图,要得到a∥b,则需条件( ).
A.∠1+∠2=180° B.∠1=∠2
C.∠1+∠2=90° D.∠1+∠2=120°
【答案】
【解析】
题干解析:
解:如图:
A、∵∠1+∠2=180°,∠3+∠2=180°,
∴∠1=∠3,
∴a∥b,故本选项正确;
B、根据∠1=∠2不能推出a∥b,故本选项错误;
C、根据∠1+∠2=90°不能推出a∥b,故本选项错误;
D、根据∠1+∠2=120°不能推出a∥b,故本选项错误;故选:A.
例2.
如图,∠1=53°,∠2=127°,∠3=53°,试说明直线AB与CD,BC与DE的位置关系.
【答案】
解:AB∥DC,CB∥DE,理由:∵∠1=53°,∠3=53°,∴∠1=∠3,∴CB∥DE,∵∠2=127°,∴∠4=53°,∴∠4=∠3,∴AB∥CD.
【解析】
题干解析:首先根据∠1=∠3可得CB∥DE,再根据邻补角互补可得∠4的度数,然后再根据∠4=∠3可得AB∥DC.
例3.
如图,已知AC⊥AE,BD⊥BF,∠1=15°,∠2=15°,证明AE∥BF.
【答案】
见解析
【解析】
题干解析:∵AC⊥AE,BD⊥BF∴∠EAC=∠FBD=90°∵∠1=15°,∠2=15°∴∠EAB=∠FBG∴AE∥BF
内错角相等,两直线平行
知识讲解
定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
?
例题精讲
内错角相等,两直线平行
例1.
如图,下列各组条件中,不能得到c∥d的是( ).
A.∠2=∠3 B.∠1+∠2=180°
C.∠2+∠4=180° D.∠2=∠5
【答案】
【解析】
题干解析:
解:A、∵∠2=∠3,
∴c∥d,正确,故A错误;
B、由∠1+∠2=180°能推出a∥b,不能推出c∥d,错误,故B正确;
C、∵∠2+∠4=180°,
∴c∥d,正确,故C错误;
D、∵∠2=∠5,
∴c∥d,正确,故D错误;故选:B.
例2.
如图,点A在直线DE上,若∠BAC= 度,则DE∥BC.
【答案】
57°
【解析】
题干解析:解:当∠BAC=57°时DE∥BC,理由是:∵∠BAC=57°,∠DAB=78°,∴∠DAC=57°+78°=135°,∵∠ACM=135°,∴∠DAC=∠ACM,∴DE∥BC,故答案为:57°.
例3.
如图,已知∠A=∠1,∠C=∠2,求证:AB∥CD.
【答案】
证明:∵∠A=∠1,∴AB∥PQ,∵∠C=∠2,∴CD∥PQ,AB∥CD.
【解析】
题干解析:先根据内错角相等,两直线平行,由∠A=∠1,∠C=∠2分别得到PQ∥AB,PQ∥CD,然后根据两条直线都和第三条直线平行,那么这两条直线平行得到结论.
同旁内角互补,两直线平行
知识讲解
定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
?
例题精讲
同旁内角互补,两直线平行
例1.
如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件( ).
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
【答案】C
【解析】
题干解析:
解:∠1=70°,要使AB∥CD,
则只要∠2=180°-70°=110°(同旁内角互补两直线平行).
故选:C.
例2.
如图,直线AB、CD与直线EF相交于E、F,∠2=65°,当∠1= 时,能使AB∥CD.
【答案】
115°
【解析】
题干解析:∠1=115°.理由是:∵∠1=115°,∴∠AEF=∠1=115°,∵∠2=65°,∴∠AEF+∠2=115°+65°=180°,∴AB∥CD.故答案为:115°.
例3.
如图,∠2+∠D=180°,∠1=∠B,那么AB∥EF吗?为什么?
【答案】
解:AB∥EF;理由如下:∵∠2+∠D=180°,∴EF∥CD,∵∠1=∠B,∴AB∥CD,∴AB∥EF.
【解析】
题干解析:由同旁内角互补得出EF∥CD,由同位角相等得出AB∥CD,即可得出AB∥EF.
平行公理推论判定平行
知识讲解
定理4:两条直线都和第三条直线平行,那么这两条直线平行.
例题精讲
平行公理推论判定平行
例1.
下列说法正确的是( ).
A.a、b、c是直线,若a⊥b,b∥c,则a∥c
B.a、b、c是直线,若a⊥b,b⊥c,则a⊥c
C.a、b、c是直线,若a∥b,b⊥c,则a∥c
D.a、b、c是直线,若a∥b,b∥c,则a∥c
【答案】
【解析】
题干解析:
根据平行线的性质和判定逐个判断即可.
两直线同垂直一条直线,则平行
知识讲解
定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
例题精讲
两直线同垂直一条直线,则平行
例1.
如图,下列条件中,能得到DG∥BC的是( ).
A.CD⊥AB,EF⊥AB
B.∠1=∠2
C.∠1=∠2,∠4+∠5=180°
D.CD⊥AB,EF⊥AB,∠1=∠2
【答案】D
【解析】
题干解析:
由平行线的判定得出A、B、C不能得到DG∥BC;由平行线的判定与性质得出D能得到DG∥BC.
解:A不能;∵CD⊥AB,EF⊥AB,
∴CD∥EF,
再没有条件得出DG∥BC;
∴A不能;
B不能,
∵∠1=∠2不能得到DG∥BC,
∴B不能;
C不能;∵∠4+∠5=180°,
∴DG∥CG,
不能得出DG∥BC,
∴C不能;
D能;∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BC,
∴D能;
故选:D.
例2.
如图,在△ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,且∠EDF=∠BDF.求证:CE是∠ACB的平分线.
【答案】
解:∵CE⊥AB,DF⊥AB,∴DF∥CE,∴∠EDF=∠DEC,∠BDF=∠BCE,∵AC∥ED,∴∠DEC=∠ACE,∵∠EDF=∠BDF,∴∠BCE=∠ACE,∴CE是∠ACB的平分线.
【解析】
题干解析:由CE与DF都与AB垂直,得到DF与CE平行,利用两直线平行内错角相等得到一对角相等,再由AC与ED平行得到一对内错角相等,等量代换得到∠EDF=∠ACE,∠BDF=∠BCE,由已知角相等,等量代换即可得证.
平行线综合判定
知识讲解
运用平行线五种判定方法综合运用。
?
例题精讲
平行线综合判定
例1.
如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( ).
A.∠1=∠2 B.∠3=∠4
C.∠5=∠B D.∠B+∠BDC=180°
【答案】A
【解析】
题干解析:
解:选项B中,∵∠3=∠4,∴AB∥CD (内错角相等,两直线平行),所以正确;
选项C中,∵∠5=∠B,∴AB∥CD (内错角相等,两直线平行),所以正确;
选项D中,∵∠B+∠BDC=180°,∴AB∥CD(同旁内角互补,两直线平行),所以正确;
而选项A中,∠1与∠2是直线AC、BD被AD所截形成的内错角,因为∠1=∠2,所以应是AC∥BD,故A错误.故选A.
例2.
已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.
【答案】
见解析
【解析】
题干解析:证明:∵BE⊥FD,∴∠EGD=90°,∴∠1+∠D=90°,又∠2和∠D互余,即∠2+∠D=90°,∴∠1=∠2,又已知∠C=∠1,∴∠C=∠2,∴AB∥CD.
例3.
如图,已知AC∥DE,CD∥EF,CD平分∠ACB.求证:
(1)∠DCB=∠CDE;
(2)EF平分∠DEB.
【答案】
证明:(1)∵AC∥DE,∴∠ACD=∠CDE,∵CD平分∠ACB,∴∠ACD=∠DCB,∴∠DCB=∠CDE;(2)∵DC∥EF,∴∠DCB=∠FEB,∠DEF=∠CDE,又由(1)知∠DCB=∠CDE,∴∠FEB=∠DCE,∴∠DEF=∠FEB,∴EF平分∠BED.
【解析】
题干解析:(1)由平行线的性质可得∠ACD=∠CDE,由角平分线的定义可得∠DCB=∠ACD,可证得结论;(2)由平行可得∠DCE=∠FEB,且∠DEF=∠EDC,结合(1)的结论,可证明EF平分∠DEB.
当堂练习
单选题
练习1.
下列叙述中,正确的是( ).
A.在同一平面内,两条直线的位置关系有三种,分别是相交、平行、垂直
B.不相交的两条直线叫平行线
C.两条直线的铁轨是平行的
D.我们知道,对顶角是相等的,那么反过来,相等的角就是对顶角
练习2.
已知直线l上有2个点A,B,点P是直线l外一点,PA=1cm,PB=2cm,有下列说法:
①点P到直线l的距离等于1cm;
②根据垂线段最短,可以判定PA⊥l;
③过点P只能画一条直线与l平行.
这些说法正确的有( ).
A.0个 B.1个 C.2个 D.3个
练习3.
在同一个平面内,不重合的两条直线的位置关系是( ).
A.平行 B.相交 C.平行或相交 D.无法确定
练习4.
下列语句:
①不相交的两条直线叫平行线
②在同一平面内,两条直线的位置关系只有两种:相交和平行
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行,那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是( ).
练习5.
如图,下列各组条件中,不能得到c∥d的是( ).
A.∠2=∠3 B.∠1+∠2=180°
C.∠2+∠4=180° D.∠2=∠5
练习6.
如图,下列说法中,正确的是( ).
A.因为∠2=∠4,所以AD∥BC
B.因为∠BAD+∠D=180°,所以AD∥BC
C.因为∠1=∠3,所以AB∥CD
D.因为∠BAD+∠B=180°,所以AD∥BC
练习7.
如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是( ).
A.∠1=∠2 B.∠3=∠4
C.∠5=∠B D.∠B+∠BDC=180°
填空题
练习1.
观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1 AB,A1A AB,A1D1 C1D1,AD BC;
(2)A1B1与BC所在的直线是两条不相交的直线,它们 平行线(填“是”或“不是”),由此可知,在 内,两条不相交的直线才能叫做平行线.
练习2.
如图,∵∠ADE=∠DEF(已知),
∴AD∥ ( ),
∵∠EFC+∠C=180°(已知),
∴EF∥ ( ),
∴ ∥ ( )
练习3.
如图,在长方体ABCD﹣EFGH中,棱AB与棱HG的位置关系是 .
练习4.
在同一平面内,如果有两条直线都与第三条直线垂直,那么这两条直线的位置关系是 .
解答题
练习1.
如图所示,已知点A、B、C,按下列要求画图:
(1)连接AB、BC、AC; (2)过点A画BC的平行线MN;
(3)过点A画BC的垂线AD,垂足为D.
练习2.
已知,如图,B、E、C在同一直线上,∠A=∠DEC,∠D=∠BEA,∠A+∠D=90°,求证:AB∥CD。?
练习3.
如图,已知∠AED=60°,∠2=30°,EF平分∠AED,可以判断EF∥BD吗?为什么?
练习4.
已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD于点G.求证:AB∥CD.
单选题:CBCBB DA
填空题
练习1:【答案】
∥,⊥,⊥,∥
平行,同一平面
练习2:【答案】
EF,内错角相等,两直线平行;BC,同旁内角互补,两直线平行;AD,BC,平行于同一条直线的两条直线平行.:
练习3:【答案】
平行
练习4:【答案】
互相平行
解答题:
练习1:【答案】
解:
【解析】
题干解析:作线段AB、AC、BC,然后利用量角器和三角板分别作出直线MN和AD即可.
练习2:【答案】
证明:∵∠A=∠DEC,∠D=∠BEA,∠A+∠D=90°∴∠DEC+∠D=90°,∴DC垂直BC,同理可证AB垂直BC∴AB∥CD。
【解析】
题干解析:等角的余角相等。垂直于同一条直线的两直线平。
练习3:【答案】
解:EF∥BD;
理由如下:
∵∠AED=60°,EF平分∠AED,
∴∠FED=30°,
又∵∠FEB=∠2=30°,
∴EF∥BD(内错角相等,两直线平行).
【解析】
题干解析:本题可通过证直线EF与BD的内错角∠1和∠2相等,来得出EF∥BD的结论.
练习4:【答案】
见解析
【解析】
题干解析:证明:∵BE⊥FD,∴∠EGD=90°,∴∠1+∠D=90°,又∠2和∠D互余,即∠2+∠D=90°,∴∠1=∠2,又已知∠C=∠1,∴∠C=∠2,∴AB∥CD.
