人教版数学七年级下册5.3.1平行线的性质学案(含答案)
文档属性
| 名称 | 人教版数学七年级下册5.3.1平行线的性质学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:18:12 | ||
图片预览



文档简介
平行线的性质
知识集结
知识元
根据平行线的性质求角的度数
知识讲解
结合图形找出平行线被直线所截得出的同位角、内错角或同旁内角,根据平行线的性质和已知中角的度数即可求出角的度数。
例题精讲
根据平行线的性质求角的度数
例1.
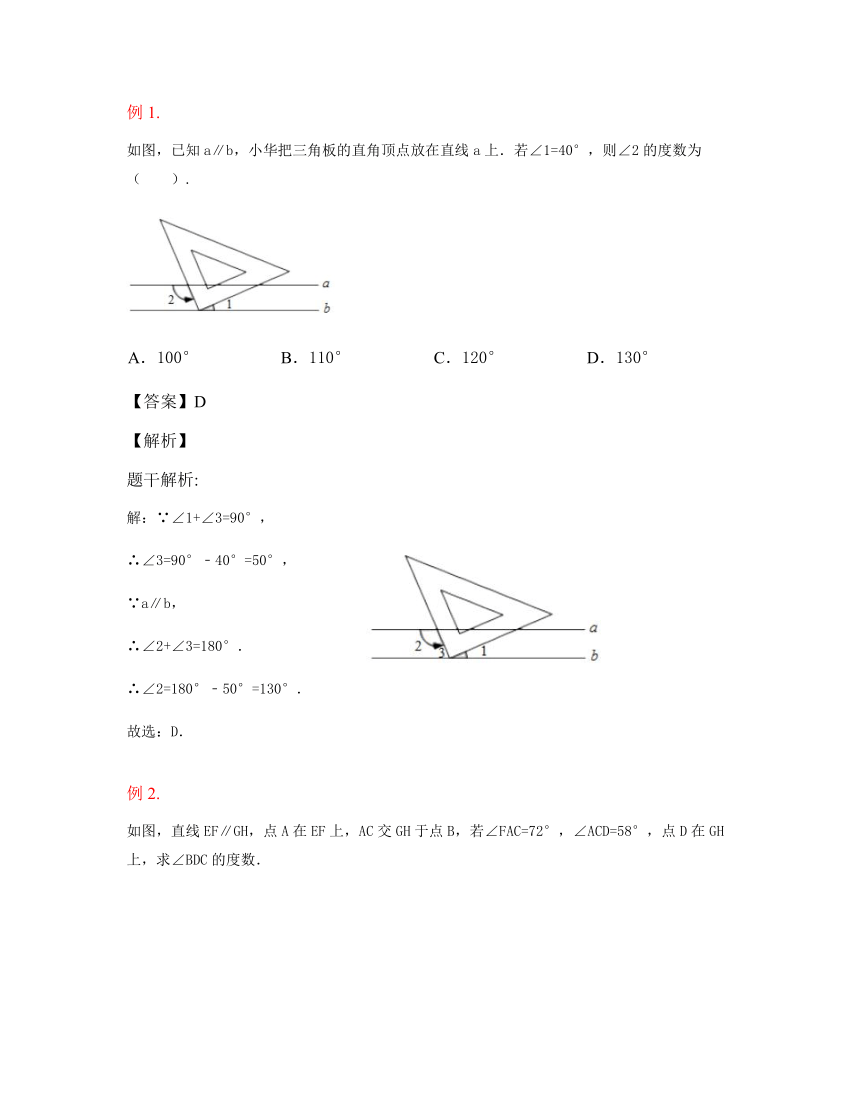
如图,已知a∥b,小华把三角板的直角顶点放在直线a上.若∠1=40°,则∠2的度数为( ).
A.100° B.110° C.120° D.130°
【答案】D
【解析】
题干解析:
解:∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故选:D.
例2.
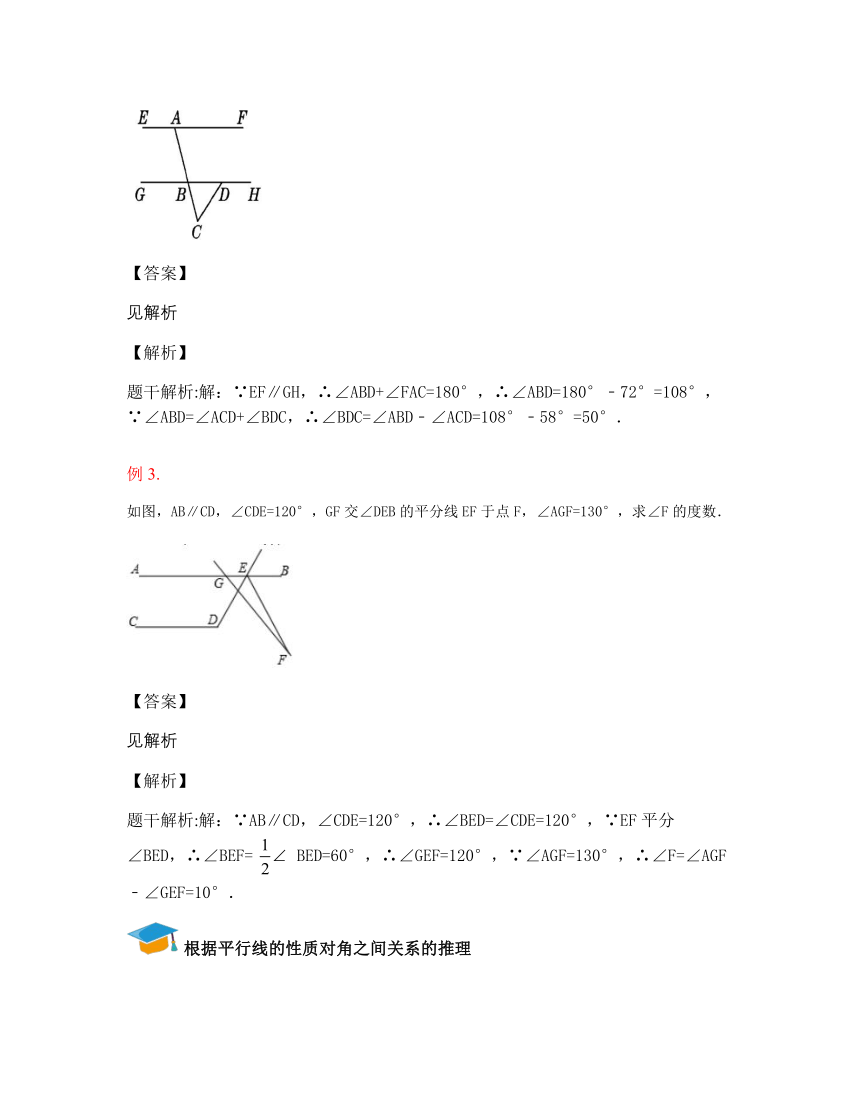
如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
【答案】
见解析
【解析】
题干解析:解:∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
例3.
如图,AB∥CD,∠CDE=120°,GF交∠DEB的平分线EF于点F,∠AGF=130°,求∠F的度数.
【答案】
见解析
【解析】
题干解析:解:∵AB∥CD,∠CDE=120°,∴∠BED=∠CDE=120°,∵EF平分∠BED,∴∠BEF= BED=60°,∴∠GEF=120°,∵∠AGF=130°,∴∠F=∠AGF﹣∠GEF=10°.
根据平行线的性质对角之间关系的推理
知识讲解
根据平行线被直线所截得的同位角相等、内错角相等,同旁内角互补,对角之间关系的进行判断。
例题精讲
根据平行线的性质对角之间关系的推理
例1.
如图,AB∥EF,EF∥CD,EG∥BD,则图中与∠1相等的角(除∠1外)共有( ).
A.6个 B.5个 C.4个 D.2个
【答案】B
【解析】
题干解析:
解:如图,与∠1相等的角有:∠2、∠3、∠4、∠5、∠6共5个.故选B.
例2.
按如图方式折叠一张对边互相平行的纸条,EF是折痕,若∠EFB=32°,则
(1)∠C′EF=32°(2)∠AEC=148°(3)∠BGE=64°(4)∠BFD=116°以上结论正确的是( ).
A.①③ B.②④ C.①③④ D.②③④
【答案】C
【解析】
题干解析:
∵AC′∥BD′,∠EFB=32°
∴∠C′EF=∠EFB=32?,故①正确;
由折叠可知,∠CEF=∠C′EF=32?,
∴∠AEC=180??∠CEF?∠C′EF=116?,故②错误;
∵AC′∥BD′,∠AEC=116?,
∴∠BGE=180??∠AEC=64?,故③正确;
∵CE∥DF,且∠BGE=∠CGF=64?,
∴∠BFD=180??∠CGF=116?,故④正确;
故选:C.
例3.
已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.问CD与AB有什么关系?
【答案】
解:CD⊥AB;理由如下:∵∠1=∠ACB,∴DE∥BC,∠2=∠DCB,又∵∠2=∠3,∴∠3=∠DCB,故CD∥FH,∵FH⊥AB∴CD⊥AB.
【解析】
题干解析:由∠1=∠ACB,利用同位角相等,两直线平行可得DE∥BC,根据平行线的性质和等量代换可得∠3=∠DCB,故推出CD∥FH,再结合已知FH⊥AB,易得CD⊥AB.
例4.
如图,已知:AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.(证明注明理由)
【答案】
证明:∵AC∥DE(已知),∴∠BCA=∠BED(两直线平行,同位角相等),即∠1+∠2=∠4+∠5,∵AC∥DE,∴∠1=∠3(两直线平行,内错角相等);∵DC∥EF(已知),∴∠3=∠4(两直线平行,内错角相等);∴∠1=∠4(等量代换),∴∠2=∠5(等式性质);∵CD平分∠BCA(已知),∴∠1=∠2(角平分线的定义),∴∠4=∠5(等量代换),∴EF平分∠BED(角平分线的定义).
【解析】
题干解析:要证明EF平分∠BED,即证∠4=∠5,由平行线的性质,∠4=∠3=∠1,∠5=∠2,只需证明∠1=∠2,而这是已知条件,故问题得证.
平行线间的距离的应用
知识讲解
(1)平行线间的距离处处相等
(2)同底等高的两个三角形的面积相等。
?
例题精讲
平行线间的距离的应用
例1.
在同一平面内,直线a∥c,且直线a到直线c的距离是2;直线b∥c,直线b到直线c的距离为5,则直线a到直线b的距离为( ).
A.3 B.7 C.3或7 D.无法确定
【答案】C
【解析】
题干解析:
此题考查了两条平行线间的距离,注意思维的严密性,应分情况考虑.分两种情况:
①直线b在直线a和c的上方;则直线a到直线b的距离为5﹣2=3;
②直线b在直线a和直线c的下方则直线a到直线b的距离为5+2=7.
综上所述,直线a到直线b的距离为3或7.故选C.
例2.
如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则△ACE的面积为 .
【答案】
8
【解析】
题干解析:根据两平行线间的距离相等,可知两个三角形的高相等,所以根据△ABD的面积可求出高,然后求△ACE的面积即可.解:在△ABD中,当BD为底时,设高为h,在△AEC中,当AE为底时,设高为h′,∵AE∥BD,∴h=h′,∵△ABD的面积为16,BD=8,∴h=4.则△ACE的面积=×4×4=8.
根据平行线的性质与判定完善简单的推理
知识讲解
理解平行线的性质与判定的区别与联系,分清性质与判定的题设与结论,是完善推理过程的关键。
例题精讲
根据平行线的性质与判定完善简单的推理
例1.
如图:∠1=∠2=∠3,完成说理过程并注明理由:
(1)因为∠1=∠2所以____∥____ ( )
(2)因为 ∠1=∠3
所以____∥____ ( )
【答案】
(1)EF BD 同位角相等两直线平行;(2)ABCD内错角相等两直线平行.
【解析】
题干解析:根据平行线的性质和判定及对顶角的性质即可得出结论。
例2.
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
(1)求证:EF∥CD;
(2)求证:∠1=∠2.
【答案】
证明:(1)∵EF⊥AB于F,CD⊥AB于D,∴∠BFE=∠BDC=90°,∴EF∥CD;(2)∵EF∥CD,∴∠2=∠3,∵∠AGD=∠ACB,∴DG∥BC,∴∠1=∠3∴∠1=∠2.
【解析】
题干解析:(1)由垂直的定义可得∠BFE=∠BDC,再根据平行线的判定可证明EF∥CD;(2)由条件可证明DG∥BC,结合(1)的结论,根据平行线的性质可证明∠1=∠2.
根据平行线的性质与判定求角的大小或判断角之间的关系
知识讲解
根据角之间的关系由平行线的判定得出平行线,根据平行线利用平行线的性质得出角之间的关系,从而求出角的大小或角之间的关系。
?
例题精讲
根据平行线的性质与判定求角的大小或判断角之间的关系
例1.
如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有( )个;若∠1=50°,则∠AHG=( )度.
【答案】
130°
【解析】
题干解析:此题主要是能够结合平行线正确找到同位角、内错角以及同旁内角.解:∵AD∥EG∥BC,AC∥EF,∴∠1=∠3,∠3=∠4,∠4=∠5,∠5=∠6,∠5=∠2.故∠1相等的角(不含∠1)有∠3,∠4,∠2,∠5,∠6共5个.∵∠1=50°,∴∠4=50°.则∠AHG=180°-50°=130°.
例2.
如图,∠1+∠2=180°,∠3=108°,求∠4的度数.
【答案】
解:∵∠3+∠6=180°,∠3=108°,∴∠6=180°-108°=72°,∵∠1+∠2=180°,∠2+∠5=180°,∴∠1=∠5,∴a∥b,∴∠4=∠6=72°.
【解析】
题干解析:先由邻补角的定义求出∠6=180°-108°=72°,再由已知,得∠1=∠5,所以a∥b,再根据两直线平行,内错角相等求∠4的度数.
例3.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
【答案】
证明:∵BD⊥AC,EF⊥AC,∴BD∥EF,∴∠2=∠CBD,∵∠2=∠1,∴∠1=∠CBD,∴GF∥BC,∵BC∥DM,∴MD∥GF,∴∠AMD=∠AGF.
【解析】
题干解析:由BD⊥AC,EF⊥AC,得到BD∥EF,根据平行线的性质得到∠2=∠CBD,等量代换得到∠1=∠CBD,根据平行线的判定定理得到GF∥BC,证得MD∥GF,根据平行线的性质即可得到结论.
根据平行线的性质与判定判断两直线平行
知识讲解
根据平行线利用平行线的性质得出角之间的关系,根据角之间的关系由平行线的判定得出平行线,从而求判断两直线平行。
例题精讲
根据平行线的性质与判定判断两直线平行
例1.
如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
【答案】
见解析
【解析】
题干解析:证明:∵AE平分∠BAD,(已知)∴∠1=∠2,(角平分线的定义)∵AB∥CD,(已知)∴∠1=∠CFE(两直线平行,同位角相等)∵∠CFE=∠E,(已知)∴∠1=∠CFE=∠E,(等量代换)∴∠2=∠E,∴AD∥BC.(内错角相等,两直线平行)
例2.
如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.
【答案】
证明:∵AE平分∠BAD,∴∠1=∠2,∵AB∥CD,∠CFE=∠E,∴∠1=∠CFE=∠E,∴∠2=∠E,∴AD∥BC.
【解析】
题干解析:首先利用平行线的性质以及角平分线的性质得到满足关于AD∥BC的条件,内错角∠2和∠E相等,得出结论.
当堂练习
单选题
练习1.
在同一平面内,直线a∥c,且直线a到直线c的距离是2;直线b∥c,直线b到直线c的距离为5,则直线a到直线b的距离为( ).
A.3 B.7 C.3或7 D.无法确定
练习2.
说法错误的是( ).
A.所有的命题都是定理 B.定理是真命题
C.公理是真命题 D.“画线段AB=CD”不是命题
练习3.
两个角的两边分别平行,其中一个角是60°,则另一个角是( ).
A.60° B.120°
C.60°或120° D.无法确定
练习4.
如图,线段AB=CD,AB与CD相交于O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是( ).
A.AC+BD>AB B.AC+BD=AB
C.AC+BD≥AB D.无法确定
练习5.
已知两个角有一条边在同一直线上,另一条边互相平行,则这两个角 ( ).
A.相等 B.互补 C.相等或互补 D.无法确定
填空题
练习1.
下列句子:
①我们到操场打球去;
②延长线段AB到C;
③对顶角相等;
④若平面上两条直线不相交,则这两条直线平行;
⑤你去看电影吗?
⑥2010年亚运会不是在广州举行;
⑦画一个角等于已知角;
⑧同位角相等吗?
这里是命题的语句是______________;是真命题的是 。
练习2.
已知,如图,直线 a∥b,则∠1,∠2,∠3,∠4 之间的数量关系为 .
解答题
练习1.
把下列命题改写成“如果……那么……”的形式,并分别指出它们的题设和结论:
(1)两点确定一条直线;
(2)同角的补角相等;
(3)两个锐角互余.
练习2.
已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD
证明:∵BE、CF分别平分∠ABC和∠BCD(已知)
∴∠1= ∠ ,∠2= ∠ ( )
∵BE∥CF( )
∴∠1=∠2( )
∴∠ABC= ∠BCD
即∠ABC=∠BCD
∴AB∥CD( )
练习3.
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
(1)求证:EF∥CD;
(2)求证:∠1=∠2.
练习4.
指出下列命题的题设和结论:
(1)等角的补角相等。
(2)有理数一定是自然数。
练习5.
如图,已知:∠1=∠2,∠D=50°,求∠B的度数.
练习6.
已知:如图,四边形ABCD中,AD⊥DC,BC⊥AB,AE平分∠BAD,CF平分∠DCB,AE交BC于E,CF交AD于F,问AE与CF是否平行?为什么?
练习7.
如图,已知直线AB∥CD,求∠A+∠C与∠AEC的大小关系并说明理由.
练习8.
如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?
练习9.
如图,BD⊥AC于D,EF⊥AC于F,DM∥BC,∠1=∠2.求证:∠AMD=∠AGF.
单选题:CACCC
填空题
练习1:【答案】
③④⑥;③④
练习2:【答案】
∠1+∠4=∠2+∠3:
解答题:
练习1【答案】
(1)如果在平面上有两个点,那么过这两个点能确定一条直线.题设:在平面上有两个点;结论:过这两个点能确定一条直线.(2)如果两个角是同角的补角,那么它们相等.题设:两个角是同角的补角;结论:这两个角相等.(3)如果两个角是锐角,那么这两个角互余.题设:两个角是锐角;结论:这两个角互余
练习2:【答案】
解:∵BE、CF分别平分∠ABC和∠BCD(已知),∴∠1= ∠ABC,∠2= ∠BCD(角平分线的定义);∵BE∥CF(已知),∴∠1=∠2(两直线平行,内错角相等),∴∠ABC= ∠BCD,即∠ABC=∠BCD,∴AB∥CD(内错角相等,两直线平行).
【解析】
题干解析:先利用角平分线的定义填空,再根据平行线的性质和判定填空.
练习3:【答案】
证明:(1)∵EF⊥AB于F,CD⊥AB于D,∴∠BFE=∠BDC=90°,∴EF∥CD;(2)∵EF∥CD,∴∠2=∠3,∵∠AGD=∠ACB,∴DG∥BC,∴∠1=∠3∴∠1=∠2.
【解析】
题干解析:(1)由垂直的定义可得∠BFE=∠BDC,再根据平行线的判定可证明EF∥CD;(2)由条件可证明DG∥BC,结合(1)的结论,根据平行线的性质可证明∠1=∠2.
练习4:【答案】
(1)题设:如果两个角相等,结论:那么这两个角是对顶角。(2)题设:如果一个数是有理数,结论:那么这个数是自然数。
【解析】
题干解析:先把命题改写为如果……那么…..的形式,如果后跟的是题设,那么后面就是结论。
练习5:【答案】
解:∵∠1=∠2,∠2=∠EHD,∴∠1=∠EHD,∴AB∥CD;∴∠B+∠D=180°,∵∠D=50°,∴∠B=180°-50°=130°.
【解析】
题干解析:此题首先要根据对顶角相等,结合已知条件,得到一组同位角相等,再根据平行线的判定得两条直线平行.然后根据平行线的性质得到同旁内角互补,从而进行求解.
练习6:【答案】
解:平行.理由如下:∵AD⊥DC,BC⊥AB,∴∠D=∠B=90°.∵∠DAB+∠B+∠BCD+∠D=360°,∴∠DAB+∠BCD=180°.∵AE平分∠BAD,CF平分∠DCB,∴∠DAE+∠DCF=90°.∵∠D+∠DFC+∠DCF=180°,∴∠DFC+∠DCF=90°.∴∠DAE=∠DFC∴AE∥CF.
【解析】
题干解析:想证明AE与CF平行需构造应用平行线判定方法的条件,∠DEA和∠DFC是直线AE与FC被直线CD所截而成的同位角,根据垂直的定义和角平分线的性质可结合图形证得∠DAE=∠DFC,再根据同位角相等,两直线平行可得AE∥CF.
练习7:【答案】
解:∠A+∠C=∠AEC.理由:过E作EF∥AB,∵EF∥AB,∴∠A=∠AEF(两直线平行内错角相等),又∵AB∥CD,EF∥AB,∴EF∥CD,∴∠C=∠CEF(两直线平行内错角相等),又∵∠AEC=∠AEF+∠CEF,∴∠AEC=∠A+∠C.
【解析】
题干解析:过E作EF∥AB,根据平行的传递性,则有EF∥CD,再根据两直线平行内错角相等的性质可求.
练习8:【答案】
平行.证明:∵CD∥AB,∴∠ABC=∠DCB=70°;又∵∠CBF=20°,∴∠ABF=∠ABC-∠CBF=70°-20°=50°;∴∠ABF+∠EFB=50°+130°=180°;∴EF∥AB(同旁内角互补,两直线平行).
【解析】
题干解析:两直线的位置关系有两种:平行和相交,根据图形可以猜想两直线平行,然后根据条件探求平行的判定条件.
练习9:【答案】
证明:∵BD⊥AC,EF⊥AC,∴BD∥EF,∴∠2=∠CBD,∵∠2=∠1,∴∠1=∠CBD,∴GF∥BC,∵BC∥DM,∴MD∥GF,∴∠AMD=∠AGF.
【解析】
题干解析:由BD⊥AC,EF⊥AC,得到BD∥EF,根据平行线的性质得到∠2=∠CBD,等量代换得到∠1=∠CBD,根据平行线的判定定理得到GF∥BC,证得MD∥GF,根据平行线的性质即可得到结论.
