人教版七年级数学 下册 5.3.1 平行线的性质 课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 5.3.1 平行线的性质 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 849.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 09:20:37 | ||
图片预览








文档简介
(共30张PPT)
名言欣赏:
数学是打开科学大门的钥匙。
——培根
平行线的判定方法有哪些?
同位角相等, 两直线平行。
内错角相等, 两直线平行。
同旁内角互补, 两直线平行。
这些判定方法先知道什么,后知道什么?
如果两条直线平行,那么这两条平行线被第三条直线所截而成的8个角会有什么关系呢?
知识回顾
5.3.1 平行线的性质
人教版七年级数学 下册
目标导航
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)。
2.能够根据平行线的性质进行简单的推理。
二、探究新知
用手中的条格纸,任意选取其中的两条线作a,b,则a∥b,再随意画一条直线c与a,b相交,如图所示,用量角器量得图中的八个角,并填表.
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
c
1
2
3
4
a
b
5
6
7
8
合作探究
二、探究新知
各对同位角、内错角、同旁内角之间有什么关系?
d
c
1
2
3
4
a
b
5
6
7
8
再任意画一条截线d,同样度量并比较各角的度数,你总结的结论还成立吗?
合作探究
1、平行线被第三条直线所截,同位角相等,
简单说成: .
2、平行线被第三条直线所截,内错角相等,
简单说成: .
3、平行线被第三条线所截,同旁内角互补,
简单说成: .
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
归纳性质
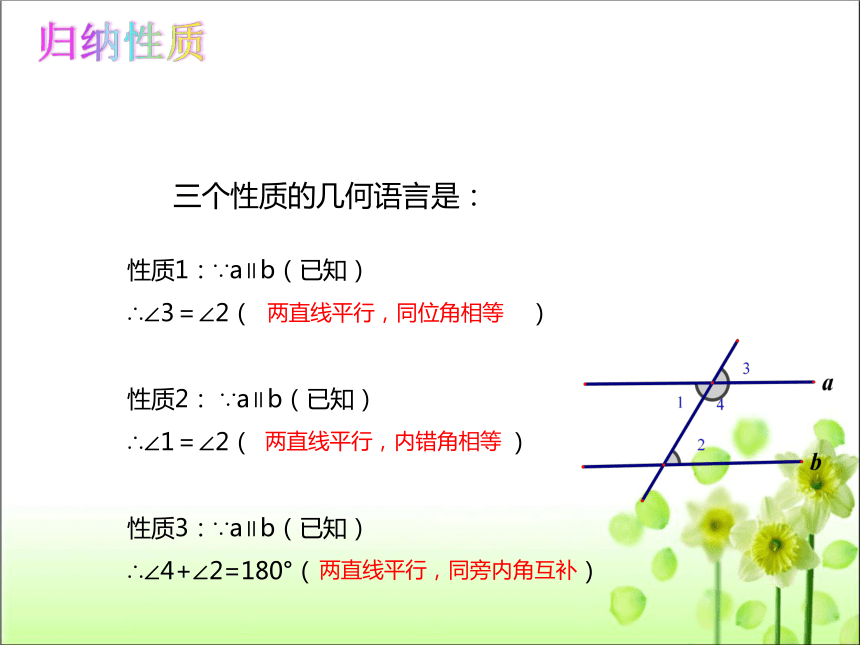
三个性质的几何语言是:
性质1:∵a∥b(已知)
∴∠3=∠2( )
性质2: ∵a∥b(已知)
∴∠1=∠2( )
性质3:∵a∥b(已知)
∴∠4+∠2=180°( )
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
归纳性质
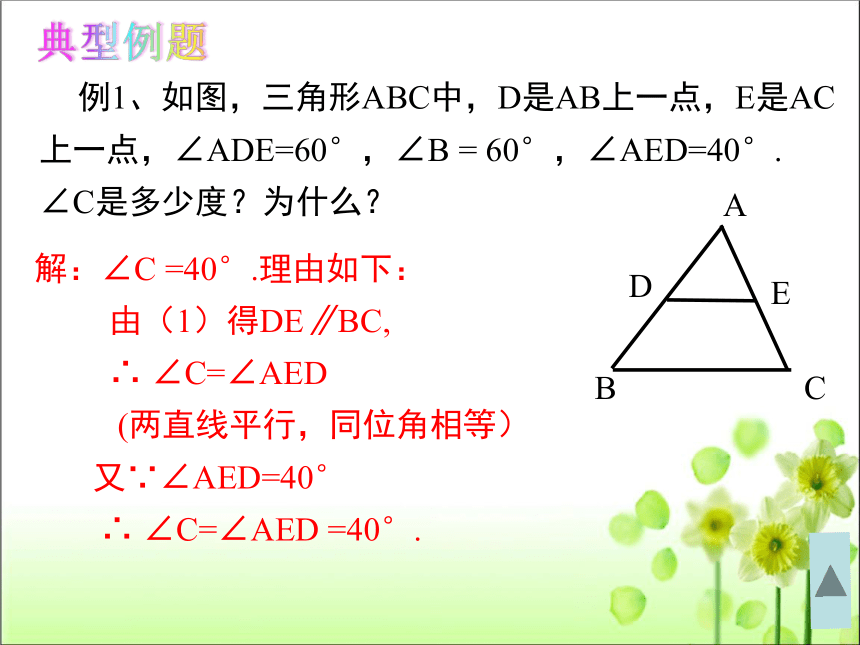
例1、如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
∠C是多少度?为什么?
C
A
B
D
E
解:∠C =40°.理由如下:
由(1)得DE∥BC,
∴ ∠C=∠AED
(两直线平行,同位角相等)
又∵∠AED=40°
∴ ∠C=∠AED =40°.
典型例题
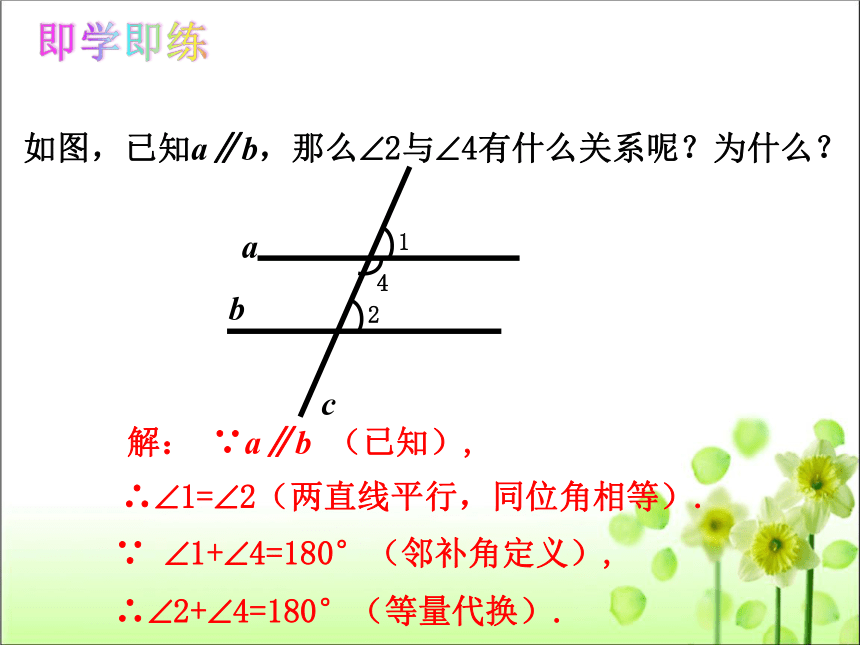
如图,已知a∥b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解: ∵a∥b (已知),
∴?1=?2(两直线平行,同位角相等).
∵ ?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
即学即练
例2、如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
理论应用
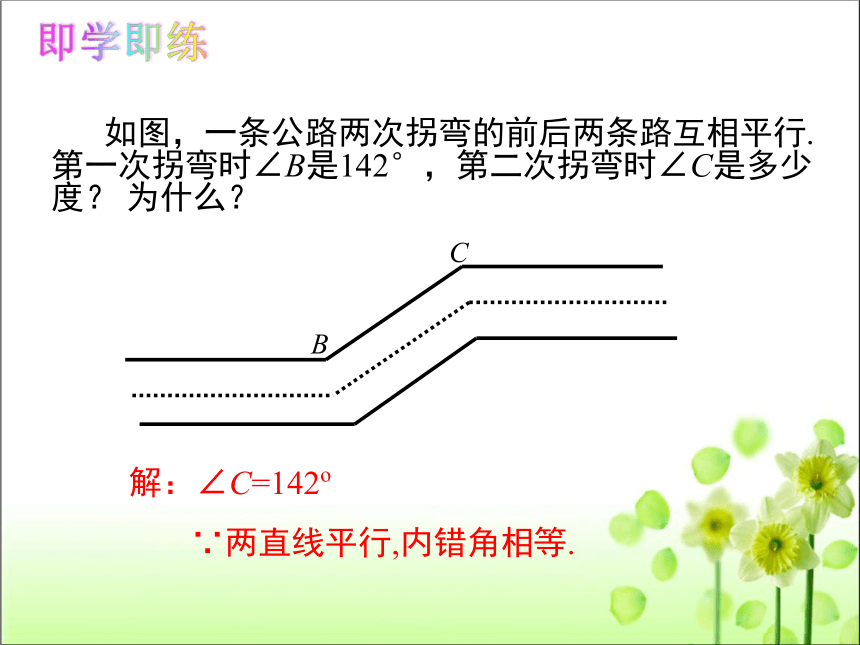
如图,一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°,第二次拐弯时∠C是多少度? 为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
即学即练
例3:如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
趣味延伸
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
变式1:
解:过点E 作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
趣味延伸
变式2:如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
趣味延伸
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = 180°
(n+1)
若有n个拐点,你能找到规律吗?
趣味延伸
五、巩固提高
画两条平行线,说出你画图的根据;再任意画一条直线和这两条平行线都相交,写出所成的角当中的一对内错角,并说明这一对内错角相等的理由.
b
2
a
c
3
解:如图,a∥b,
根据:利用同位角相等,两直线平行画图;
∠3和∠2是内错角, ∠3=∠2,
理由:两直线平行,内错角相等.
即学即练
解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
有这样一道题:如图2,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据。
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
即学即练
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的判定与性质
课堂小结
1.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
检测目标
2. 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
C
解:(1) DE∥BC.理由如下:
∵ ∠ADE=60°,∠B = 60°
∴ ∠ADE=∠B
∴ DE∥BC
(同位角相等,两直线平行 ).
A
B
D
E
检测目标
3.如图,直线a∥b,∠1=54°,∠2 ,∠3 ,∠4各是多少度 ?
解: ∵∠1=54°,
∴ ∠2=∠1=54°.
∵a∥b,
∴ ∠2+∠3=180°(两直线平行,同旁内角互补),
∴ ∠3=180°-∠2=180°-54°=126°.
∵a∥b ,
∴∠4=∠2=54°(两直线平行,内错角相等).
检测目标
五、巩固提高
4.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(1)∵ a∥b,
∴∠1=∠3( ).
a
b
c
1
2
3
4
两直线平行,同位角相等
(2)∵ ∠1= ∠3,
∴a∥b( ).
同位角相等,两直线平行
(3)∵a∥b ,
∴∠1=∠2( ).
两直线平行,内错角相等
检测目标
五、巩固提高
4.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(4)∵ a∥b,
∴∠1+∠4=180°( ).
a
b
c
1
2
3
4
两直线平行,同旁内角互补
(5)∵ ∠1= ∠2,
∴a∥b( ).
内错角相等,两直线平行
(6)∵∠1+∠4=180° ,
∴ a∥b( ____ ).
同旁内角互补,两直线平行
检测目标
5.如图,BCD是一条直线,∠A=75°, ∠1=53°,∠2=75°,求∠B的度数.
B
A
C
D
E
1
2
解: ∵∠A=∠2=75°,
∴AB∥CE,
∴∠B=∠1=53°.
检测目标
6.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
名言欣赏:
数学是打开科学大门的钥匙。
——培根
平行线的判定方法有哪些?
同位角相等, 两直线平行。
内错角相等, 两直线平行。
同旁内角互补, 两直线平行。
这些判定方法先知道什么,后知道什么?
如果两条直线平行,那么这两条平行线被第三条直线所截而成的8个角会有什么关系呢?
知识回顾
5.3.1 平行线的性质
人教版七年级数学 下册
目标导航
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)。
2.能够根据平行线的性质进行简单的推理。
二、探究新知
用手中的条格纸,任意选取其中的两条线作a,b,则a∥b,再随意画一条直线c与a,b相交,如图所示,用量角器量得图中的八个角,并填表.
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
c
1
2
3
4
a
b
5
6
7
8
合作探究
二、探究新知
各对同位角、内错角、同旁内角之间有什么关系?
d
c
1
2
3
4
a
b
5
6
7
8
再任意画一条截线d,同样度量并比较各角的度数,你总结的结论还成立吗?
合作探究
1、平行线被第三条直线所截,同位角相等,
简单说成: .
2、平行线被第三条直线所截,内错角相等,
简单说成: .
3、平行线被第三条线所截,同旁内角互补,
简单说成: .
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
归纳性质
三个性质的几何语言是:
性质1:∵a∥b(已知)
∴∠3=∠2( )
性质2: ∵a∥b(已知)
∴∠1=∠2( )
性质3:∵a∥b(已知)
∴∠4+∠2=180°( )
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
归纳性质
例1、如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
∠C是多少度?为什么?
C
A
B
D
E
解:∠C =40°.理由如下:
由(1)得DE∥BC,
∴ ∠C=∠AED
(两直线平行,同位角相等)
又∵∠AED=40°
∴ ∠C=∠AED =40°.
典型例题
如图,已知a∥b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解: ∵a∥b (已知),
∴?1=?2(两直线平行,同位角相等).
∵ ?1+?4=180°(邻补角定义),
∴?2+?4=180°(等量代换).
即学即练
例2、如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
理论应用
如图,一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°,第二次拐弯时∠C是多少度? 为什么?
解:∠C=142o
∵两直线平行,内错角相等.
B
C
即学即练
例3:如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法.
B
D
C
E
A
解:过点E 作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
趣味延伸
如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
变式1:
解:过点E 作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
趣味延伸
变式2:如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有一个拐点时: ∠A+∠E+∠C= 360°
当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
趣味延伸
…
A
B
C
D
E1
E2
En
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = 180°
(n+1)
若有n个拐点,你能找到规律吗?
趣味延伸
五、巩固提高
画两条平行线,说出你画图的根据;再任意画一条直线和这两条平行线都相交,写出所成的角当中的一对内错角,并说明这一对内错角相等的理由.
b
2
a
c
3
解:如图,a∥b,
根据:利用同位角相等,两直线平行画图;
∠3和∠2是内错角, ∠3=∠2,
理由:两直线平行,内错角相等.
即学即练
解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
有这样一道题:如图2,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据。
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
即学即练
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
平行线的判定与性质
课堂小结
1.直线a,b与直线c相交,给出下列条件:
①∠1= ∠2; ②∠3= ∠6;
③∠4+∠7=180o; ④∠3+ ∠5=180°,
其中能判断a//b的是( )
A. ①②③④
B .①③④
C. ①③
D. ④
1
2
3
4
5
6
7
8
c
a
b
B
检测目标
2. 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
C
解:(1) DE∥BC.理由如下:
∵ ∠ADE=60°,∠B = 60°
∴ ∠ADE=∠B
∴ DE∥BC
(同位角相等,两直线平行 ).
A
B
D
E
检测目标
3.如图,直线a∥b,∠1=54°,∠2 ,∠3 ,∠4各是多少度 ?
解: ∵∠1=54°,
∴ ∠2=∠1=54°.
∵a∥b,
∴ ∠2+∠3=180°(两直线平行,同旁内角互补),
∴ ∠3=180°-∠2=180°-54°=126°.
∵a∥b ,
∴∠4=∠2=54°(两直线平行,内错角相等).
检测目标
五、巩固提高
4.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(1)∵ a∥b,
∴∠1=∠3( ).
a
b
c
1
2
3
4
两直线平行,同位角相等
(2)∵ ∠1= ∠3,
∴a∥b( ).
同位角相等,两直线平行
(3)∵a∥b ,
∴∠1=∠2( ).
两直线平行,内错角相等
检测目标
五、巩固提高
4.如图,已知直线a,b被直线c所截,在括号内为下面各小题推理填上适当的根据:
(4)∵ a∥b,
∴∠1+∠4=180°( ).
a
b
c
1
2
3
4
两直线平行,同旁内角互补
(5)∵ ∠1= ∠2,
∴a∥b( ).
内错角相等,两直线平行
(6)∵∠1+∠4=180° ,
∴ a∥b( ____ ).
同旁内角互补,两直线平行
检测目标
5.如图,BCD是一条直线,∠A=75°, ∠1=53°,∠2=75°,求∠B的度数.
B
A
C
D
E
1
2
解: ∵∠A=∠2=75°,
∴AB∥CE,
∴∠B=∠1=53°.
检测目标
6.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:
∵EF∥AD,
(已知)
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DG∥AB.
∴∠BAC+∠AGD=180°.
∴∠AGD=180°-∠BAC=180°-70°=110°.
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
D
A
G
C
B
E
F
1
3
2
检测目标
我们已经站在了人生的起跑线上,为了实现心中的远大目标,我们正努力拼搏着。成功属于不畏困难、勇往直前的人。相信自己!
教师寄语
通过本课学习,你收获了什么?
课后作业:
完成教科书中相关练习题。
