华东师大版八年级数学下册17章 函数及其图象 小结与复习课件(共40张PPT)
文档属性
| 名称 | 华东师大版八年级数学下册17章 函数及其图象 小结与复习课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 425.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
小结与复习
第17章 函数及其图象
要点梳理
1. 常量与变量
叫变量,
叫常量.
2.函数定义:
取值发生变化的量
取值固定不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析法
图象法.
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
一次函数 一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数 特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,这样的函数称为分段函数.
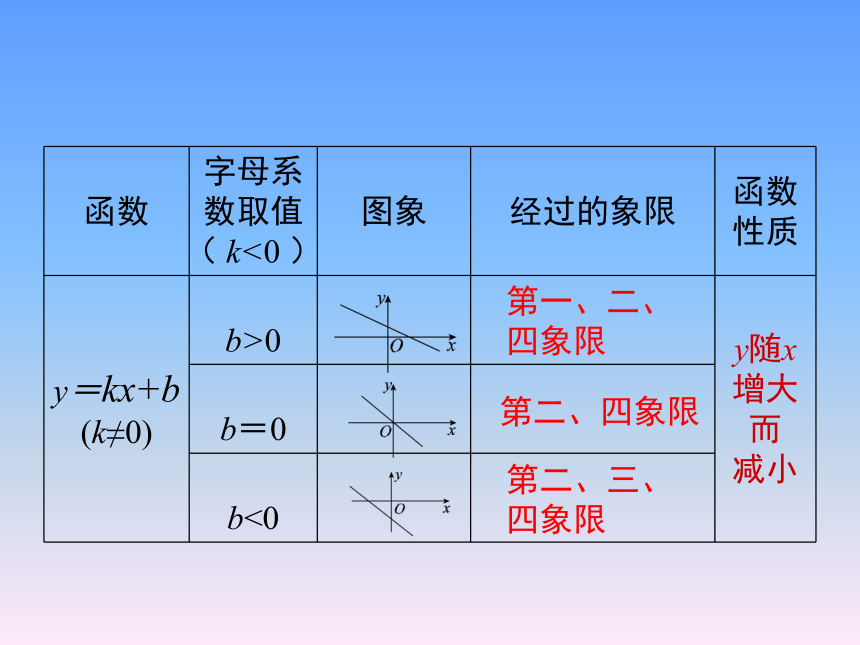
函数 字母系数取值
( k>0 ) 图象 经过的象限 函数性质
y=kx+b
(k≠0) b>0 y随x增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
3.一次函数的图象与性质
函数 字母系数取值
( k<0 ) 图象 经过的象限 函数性质
y=kx+b
(k≠0) b>0 y随x增大而
减小
b=0
b<0
第一、二、
四象限
第二、四象限
第二、三、
四象限
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
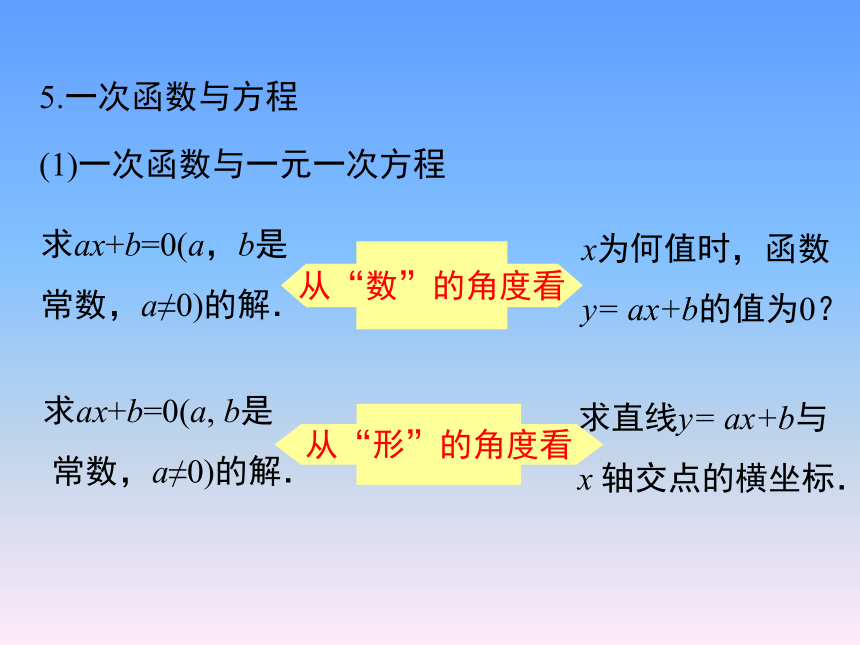
4.用待定系数法求一次函数的解析式
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时,函数
y= ax+b的值为0?
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b与
x 轴交点的横坐标.
从“形”的角度看
(1)一次函数与一元一次方程
5.一次函数与方程
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)一次函数与二元一次方程
方程的解 对应直线点的坐标.
1. 反比例函数的概念
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表示方法: 或 xy=k 或y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
三、反比例函数
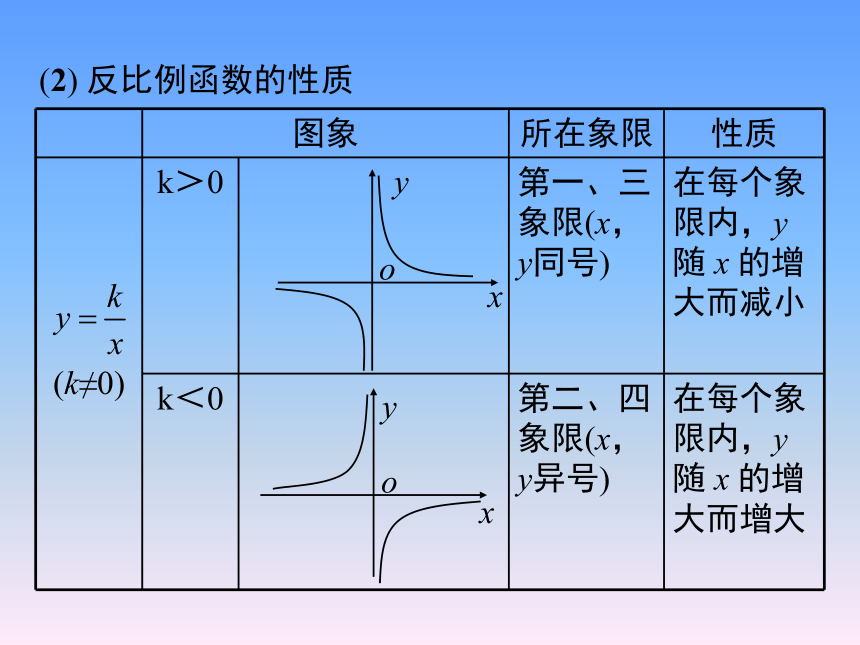
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是轴对称图形又是中心
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
(2) 反比例函数的性质
图象 所在象限 性质
(k≠0) k>0 第一、三象限(x,y同号) 在每个象限内,y 随 x 的增大而减小
k<0 第二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值,求出 k 的值;
③ 写出解析式.
考点讲练
考点一 函数的有关概念及图象
例1 王大爷饭后出去散步,从家中走20分钟到离家900米的公园,与朋友聊天10分钟后,用15分钟返回家中.下面图形表示王大爷离家时间x(分)与离家距离y(米)之间的关系是( )
A
B
C
D
D
O
O
O
O
针对训练
1.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的周长与面积
C.等腰三角形的底边长与面积
D.圆的周长与半径
C
2.函数 中,自变量x的取值范围是( )
A.x>3 B.x<3 C.x≤3 D.x≥-3
B
3.星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(千米)和所用的时间x(分)之间的函数关系图象.下列说法错误的是( )
A.小强从家到公共汽车站步行了2千米
B.小强在公共汽车站等小明用了10分钟
C.公交车的平均速度是34千米/时
D.小强乘公交车用了30分钟
C
x(分)
y(千米)
考点二 一次函数的图象与性质
例2 已知函数y=(2m+1)x+m﹣3;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0;(2)由两直线平行得2m+1=3;(3)一次函数中y随着x的增大而减小,即2m+1<0;(4)代入该点坐标即可求解.
解:(1)∵函数是正比例函数,∴m﹣3=0,且2m+1≠0,
解得m=3;
(2)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1;
(3)∵y随着x的增大而减小,∴2m+1<0,解得m< ???.
(4)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴该函数的解析式为y=5x-1.
一次函数y=kx+b中b=0时,该函数为正比例函数;两条直线平行,其函数解析式中的自变量系数k相等;当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.
方法总结
针对训练
4.一次函数y=-5x+2的图象不经过第______象限.
5.点(-1,y1),(2,y2)是直线y=2x+1上两点,则y1____y2.
三
<
6.填空题:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数y
随x的增大而增大的是_____;函数y随x的增大而减小
的是_____;图象在第一、二、三象限的是______.
②
③
④
①③
x
y
2
=
考点三 一次函数与一次方程
例3 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的方程x+b=kx+4的解是( )
y
x
O
y1=x+b
y2=kx+4
P
A.x=﹣2 B.x=0
C.x=1 D.x=-1
【分析】观察图象,两图象交点为
P(1,3),当x=1时,y1=y2,
据此解题即可.
1
3
C
针对训练
7.方程x+2=0的解就是函数y=x+2的图象与( )
A.x轴交点的横坐标 B.y轴交点的横坐标
C.y轴交点的纵坐标 D.以上都不对
8.两个一次函数y=-x+5和y=-2x+8的图象的交点坐标是 _________.
A
(3,2)
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例4 为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
考点四 一次函数的应用
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42720(元).
即最低成本是 42720 元.
用一次函数解决实际问题,先理解清楚题意,把文字语言转化为数学语言,列出相应的不等式(方程),若是方案选择问题,则要求出自变量在取不同值时所对应的函数值,判断其大小关系,结合实际需求,选择最佳方案.
方法总结
9.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是多少升?
针对训练
解:设一次函数的解析式为y=kx+35,
将(160,25)代入,得160k+35=25,
解得k= ,
所以一次函数的解析式为y= x+35.
再将x=240代入 y= x+35,
得y= ×240+35=20,
即到达乙地时油箱剩余油量是20升.
10.小星以2米/秒的速度起跑后,先匀速跑5秒,然后突然把速度提高4米/秒,又匀速跑5秒.试写出这段时间里他的跑步路程s(单位:米)随跑步时间x(单位:秒)变化的函数关系式,并画出函数图象.
解:依题意得
s={
2x
(0≤x≤5)
6x-20
(510
0
s(米)
5
0
x(秒)
①
40
10
s(米)
10
5
x(秒)
②
x(秒)
s(米)
O
·
·
·
·
5
10
10
40
·
·
·
s=2x (0≤x≤5)
s=6x-20 (5例5 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
解析:方法①分别把各点代入反比例函数求出y1,y2,
y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
考点五 反比例函数的图象和性质
D
11. 已知点 A (x1,y1),B (x2,y2) (x1<0<x2)都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
y1 >0>y2
针对训练
例6 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:因为当 0 ≤ x ≤2 时,y 与 x 成
正比例关系.
所以设 y =kx,由于点 (2,4)
在该线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例关系,
所以设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有
效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
12.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到
28℃时停止加热,停止加热
后,材料温度逐渐下降,这
时温度y与时间 x 成反比例
函数关系,已知第 12 分钟
时,材料温度是14℃.
针对训练
O
y(℃)
x(min)
12
4
14
28
(1) 分别求出该材料加热和停止加热过程中 y 与 x 的函
数关系式(写出x的取值范围);
O
y(℃)
x(min)
12
4
14
28
答案:
y =
4x + 4 (0 ≤ x ≤ 6),
(x>6).
(2) 根据该食品制作要求,在材料温度不低于 12℃ 的
这段时间内,需要对该材料进行特殊处理,那么
对该材料进行特殊处理的时间为多少分钟?
解:当y =12时,y =4x+4,解得 x=2.
由 ,解得x =14.
所以对该材料进行特殊
处理所用的时间为
14-2=12 (分钟).
O
y(℃)
x(min)
12
4
14
28
课堂小结
实际问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与一次方程之间的关系
课堂小结
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
小结与复习
第17章 函数及其图象
要点梳理
1. 常量与变量
叫变量,
叫常量.
2.函数定义:
取值发生变化的量
取值固定不变的量
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
一、函数
3.函数的图象:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法
解析法
图象法.
5.函数的三种表示方法:
4.描点法画图象的步骤:列表、描点、连线
一次函数 一般地,如果y= k x+b (k、b是常数,k≠0),那么y叫做x的一次函数.
正比例函数 特别地,当b=____时,一次函数y=k x+b变为y= _____(k为常数,k≠0),这时y叫做x的正比例函数.
0
kx
二、一次函数
1.一次函数与正比例函数的概念
2.分段函数
当自变量的取值范围不同时,函数的解析式也不同,这样的函数称为分段函数.
函数 字母系数取值
( k>0 ) 图象 经过的象限 函数性质
y=kx+b
(k≠0) b>0 y随x增大而
增大
b=0
b<0
第一、三象限
第一、二、三象限
第一、三、四象限
3.一次函数的图象与性质
函数 字母系数取值
( k<0 ) 图象 经过的象限 函数性质
y=kx+b
(k≠0) b>0 y随x增大而
减小
b=0
b<0
第一、二、
四象限
第二、四象限
第二、三、
四象限
求一次函数解析式的一般步骤:
(1)先设出函数解析式;
(2)根据条件列关于待定系数的方程(组);
(3)解方程(组)求出解析式中未知的系数;
(4)把求出的系数代入设的解析式,从而具体写出这个解析式.这种求解析式的方法叫待定系数法.
4.用待定系数法求一次函数的解析式
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时,函数
y= ax+b的值为0?
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b与
x 轴交点的横坐标.
从“形”的角度看
(1)一次函数与一元一次方程
5.一次函数与方程
一般地,任何一个二元一次方程都可以转化为一次函数y=kx+b(k、b为常数,且k≠0)的形式,所以每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)一次函数与二元一次方程
方程的解 对应直线点的坐标.
1. 反比例函数的概念
定义:形如________ (k为常数,k≠0) 的函数称为反
比例函数,其中x是自变量,y是x的函数,k是比例
系数.
三种表示方法: 或 xy=k 或y=kx-1 (k≠0).
防错提醒:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
三、反比例函数
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k≠0)的
图象是 ,它既是轴对称图形又是中心
对称图形.
反比例函数的两条对称轴为直线 和 ;
对称中心是: .
双曲线
原点
y = x
y=-x
(2) 反比例函数的性质
图象 所在象限 性质
(k≠0) k>0 第一、三象限(x,y同号) 在每个象限内,y 随 x 的增大而减小
k<0 第二、四象限(x,y异号)
在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
(3) 反比例函数比例系数 k 的几何意义
k 的几何意义:反比例函数图象上的点 (x,y) 具有
两坐标之积 (xy=k) 为常数这一特点,即过双曲线
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 |k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
?利用待定系数法确定反比例函数:
① 根据两变量之间的反比例关系,设 ;
② 代入图象上一个点的坐标,即 x、y 的一对
对应值,求出 k 的值;
③ 写出解析式.
考点讲练
考点一 函数的有关概念及图象
例1 王大爷饭后出去散步,从家中走20分钟到离家900米的公园,与朋友聊天10分钟后,用15分钟返回家中.下面图形表示王大爷离家时间x(分)与离家距离y(米)之间的关系是( )
A
B
C
D
D
O
O
O
O
针对训练
1.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的周长与面积
C.等腰三角形的底边长与面积
D.圆的周长与半径
C
2.函数 中,自变量x的取值范围是( )
A.x>3 B.x<3 C.x≤3 D.x≥-3
B
3.星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(千米)和所用的时间x(分)之间的函数关系图象.下列说法错误的是( )
A.小强从家到公共汽车站步行了2千米
B.小强在公共汽车站等小明用了10分钟
C.公交车的平均速度是34千米/时
D.小强乘公交车用了30分钟
C
x(分)
y(千米)
考点二 一次函数的图象与性质
例2 已知函数y=(2m+1)x+m﹣3;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行于直线y=3x﹣3,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
【分析】(1)由函数是正比例函数得m-3=0且2m+1≠0;(2)由两直线平行得2m+1=3;(3)一次函数中y随着x的增大而减小,即2m+1<0;(4)代入该点坐标即可求解.
解:(1)∵函数是正比例函数,∴m﹣3=0,且2m+1≠0,
解得m=3;
(2)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1;
(3)∵y随着x的增大而减小,∴2m+1<0,解得m< ???.
(4)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴该函数的解析式为y=5x-1.
一次函数y=kx+b中b=0时,该函数为正比例函数;两条直线平行,其函数解析式中的自变量系数k相等;当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.
方法总结
针对训练
4.一次函数y=-5x+2的图象不经过第______象限.
5.点(-1,y1),(2,y2)是直线y=2x+1上两点,则y1____y2.
三
<
6.填空题:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数y
随x的增大而增大的是_____;函数y随x的增大而减小
的是_____;图象在第一、二、三象限的是______.
②
③
④
①③
x
y
2
=
考点三 一次函数与一次方程
例3 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的方程x+b=kx+4的解是( )
y
x
O
y1=x+b
y2=kx+4
P
A.x=﹣2 B.x=0
C.x=1 D.x=-1
【分析】观察图象,两图象交点为
P(1,3),当x=1时,y1=y2,
据此解题即可.
1
3
C
针对训练
7.方程x+2=0的解就是函数y=x+2的图象与( )
A.x轴交点的横坐标 B.y轴交点的横坐标
C.y轴交点的纵坐标 D.以上都不对
8.两个一次函数y=-x+5和y=-2x+8的图象的交点坐标是 _________.
A
(3,2)
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例4 为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
考点四 一次函数的应用
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值为
33×800+17×960=42720(元).
即最低成本是 42720 元.
用一次函数解决实际问题,先理解清楚题意,把文字语言转化为数学语言,列出相应的不等式(方程),若是方案选择问题,则要求出自变量在取不同值时所对应的函数值,判断其大小关系,结合实际需求,选择最佳方案.
方法总结
9.李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是多少升?
针对训练
解:设一次函数的解析式为y=kx+35,
将(160,25)代入,得160k+35=25,
解得k= ,
所以一次函数的解析式为y= x+35.
再将x=240代入 y= x+35,
得y= ×240+35=20,
即到达乙地时油箱剩余油量是20升.
10.小星以2米/秒的速度起跑后,先匀速跑5秒,然后突然把速度提高4米/秒,又匀速跑5秒.试写出这段时间里他的跑步路程s(单位:米)随跑步时间x(单位:秒)变化的函数关系式,并画出函数图象.
解:依题意得
s={
2x
(0≤x≤5)
6x-20
(5
0
s(米)
5
0
x(秒)
①
40
10
s(米)
10
5
x(秒)
②
x(秒)
s(米)
O
·
·
·
·
5
10
10
40
·
·
·
s=2x (0≤x≤5)
s=6x-20 (5
例函数 的图象上,则y1,y2,y3的大小关系是
( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
解析:方法①分别把各点代入反比例函数求出y1,y2,
y3的值,再比较出其大小即可.
方法②:根据反比例函数的图象和性质比较.
考点五 反比例函数的图象和性质
D
11. 已知点 A (x1,y1),B (x2,y2) (x1<0<x2)都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
y1 >0>y2
针对训练
例6 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0 ≤ x ≤2 时,y 与 x 的函数解析式;
解:因为当 0 ≤ x ≤2 时,y 与 x 成
正比例关系.
所以设 y =kx,由于点 (2,4)
在该线段上,
所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数解析式;
解:当 x > 2时,y 与 x 成反比例关系,
所以设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有
效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,
解得x≥1,∴1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥ 2,解得 x ≤ 4. ∴2< x ≤4.
所以服药一次,治疗疾病的有
效时间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
12.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到
28℃时停止加热,停止加热
后,材料温度逐渐下降,这
时温度y与时间 x 成反比例
函数关系,已知第 12 分钟
时,材料温度是14℃.
针对训练
O
y(℃)
x(min)
12
4
14
28
(1) 分别求出该材料加热和停止加热过程中 y 与 x 的函
数关系式(写出x的取值范围);
O
y(℃)
x(min)
12
4
14
28
答案:
y =
4x + 4 (0 ≤ x ≤ 6),
(x>6).
(2) 根据该食品制作要求,在材料温度不低于 12℃ 的
这段时间内,需要对该材料进行特殊处理,那么
对该材料进行特殊处理的时间为多少分钟?
解:当y =12时,y =4x+4,解得 x=2.
由 ,解得x =14.
所以对该材料进行特殊
处理所用的时间为
14-2=12 (分钟).
O
y(℃)
x(min)
12
4
14
28
课堂小结
实际问题
函数
建立函
数模型
定义
自变量取值范围
表示法
一次函数
y=kx+b(k≠0)
应用
图象:一条直线
性质:
k>0,y 随x 的增大而增大
k<0,y 随x 的增大而减小
数形结合
一次函数与一次方程之间的关系
课堂小结
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
