人教版九年级数学下册 26.1 反比例函数 同步练习含答案
文档属性
| 名称 | 人教版九年级数学下册 26.1 反比例函数 同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 10:22:48 | ||
图片预览



文档简介
反比例函数 同步练习
1、填空题
1、反比例函数的图象在第二、四象限,那么实数的取值范围是???????? ??
2、.若A(-3,y1),B(-2,y2),C(1,y3)三点都在函数y=-的图象上,则y1,y2,y3的大小关系是(用“<”连接)???????
3、已知:点P(m,n)在直线y=-x+2上,也在双曲线y=-上,则m2+n2的值为???????? ??
4、如图,直线y=x+2与双曲线y=相交于点A(m,3),与x轴交于点C.点P在x轴上,如果△ACP的面积为3,则点P的坐标是???????? ??
5、.若点A坐标(3,2)点B是x轴正半轴上的动点,点C是反比例图像上的动点。若△ABC为等腰直角三角形,则点B的坐标是?????
6、如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与正比例函数y=kx,y=x(k>1)的图象分别交于点A,B,若∠AOB=45°,则△AOB的面积是???????? ??
二、选择题
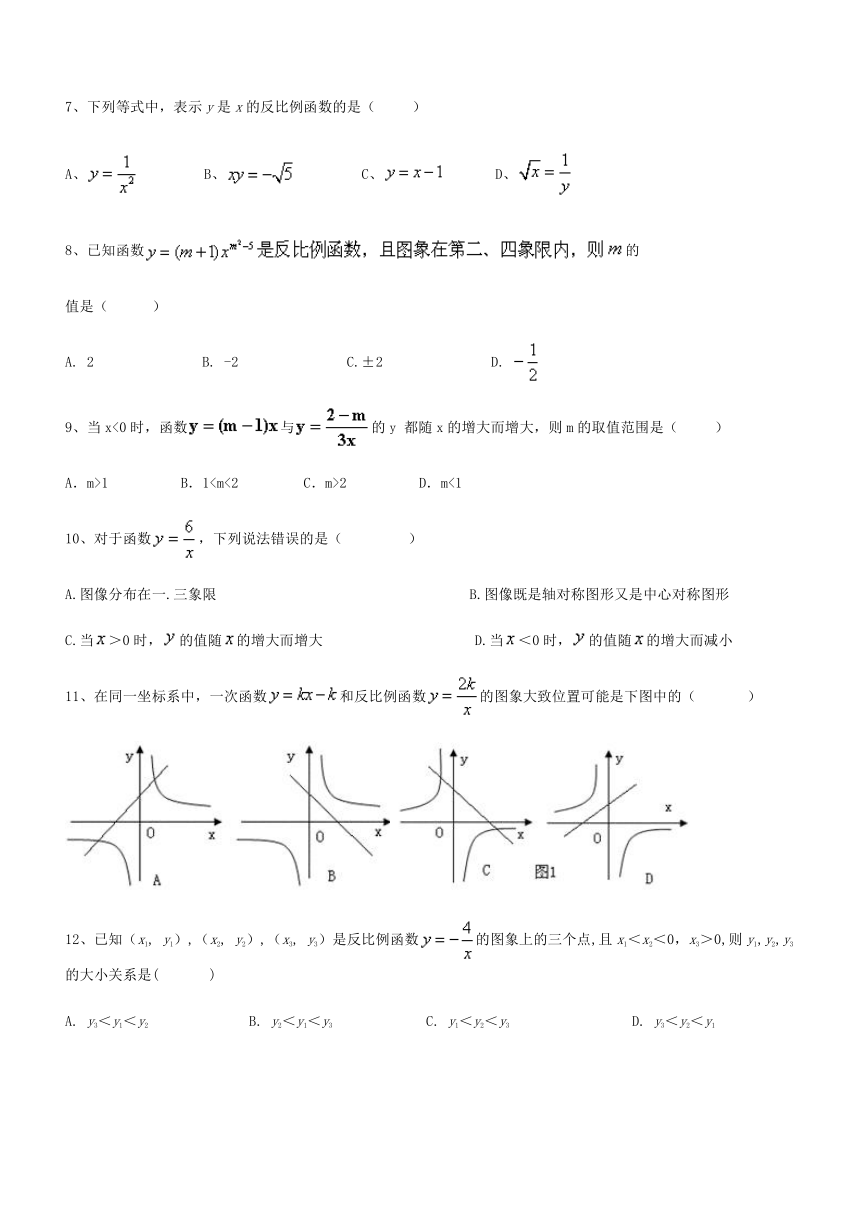
7、下列等式中,表示y是x的反比例函数的是(?? )
A、??? ?B、 ????C、? ??D、
8、已知函数的
值是( )
A. 2??????? B. -2??????? C.±2??????? D.
9、当x<0时,函数与的y 都随x的增大而增大,则m的取值范围是(?? )
A.m>1?? B.1
10、对于函数,下列说法错误的是(???? )
A.图像分布在一.三象限????????????????? B.图像既是轴对称图形又是中心对称图形
C.当>0时,的值随的增大而增大??? ? D.当<0时,的值随的增大而减小
11、在同一坐标系中,一次函数和反比例函数的图象大致位置可能是下图中的(??? )
12、已知(x1, y1),(x2, y2),(x3, y3)是反比例函数的图象上的三个点,且x1<x2<0,x3>0,则y1,y2,y3的大小关系是(??? )
A. y3<y1<y2?? ???? B. y2<y1<y3? ?????C. y1<y2<y3???? ????D. y3<y2<y1
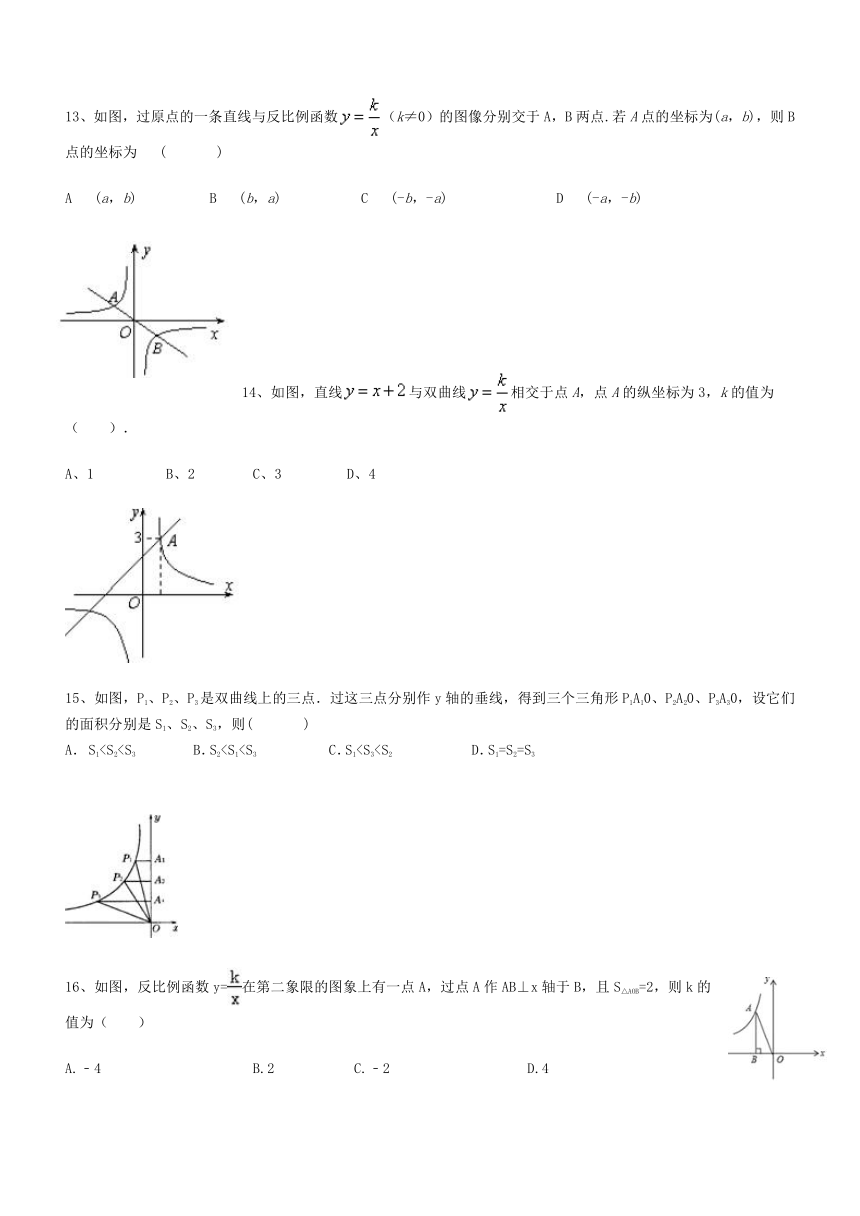
13、如图,过原点的一条直线与反比例函数(k≠0)的图像分别交于A,B两点.若A点的坐标为(a,b),则B点的坐标为? (??? )
A ?(a,b)?? ? ?B ?(b,a)???? ?C ?(-b,-a)?????? ?D ?(-a,-b)
14、如图,直线与双曲线相交于点A,点A的纵坐标为3,k的值为( ).
A、1 B、2 C、3 D、4
15、如图,P1、P2、P3是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形P1A10、P2A20、P3A30,设它们的面积分别是S1、S2、S3,则(??? ) A. S1
16、如图,反比例函数y=在第二象限的图象上有一点A,过点A作AB⊥x轴于B,且S△AOB=2,则k的值为( )
A.﹣4?????????? B.2????? C.﹣2????????? D.4
17如图,正比例函数与反比例函数的图象交于,两点,轴于点,连接,则的面积为( )
A. ???? B. ??? ?C. ??? ?D.
17、如图,已知四边形是菱形,轴,垂足为,函数的图象经过点,且与交于点.若,则的面积为( )
A. ???? B. ??? ?C. ?? ??D.
三、简答题
19、已知是的反比例函数,当=3时,=5.
(1)写出与的函数关系式;
(2)求当=5时,的值.
20、在平面直角坐标系中,反比例函数的图象与的图象关于轴对称,又与直线交于点,试确定的值.
21、如图,一次函数和反比例函数的图像交于A、B两点.
(1)利用图中条件,求出两个函数的解析式;
(2)根据图像写出使一次函数的值大于反比例函数的值的x的取值范围.
22、如图,E是正方形ABCD的边AD上的动点,F是边BC延长线上的一点,且BF=EF,AB=12,设AE=x,BF=y.
(1)当△BEF是等边三角形时,求BF的长;
(2)求y与x之间的函数解析式,并写出它的定义域;
(3)把△ABE沿着直线BE翻折,点A落在点处,试探索:△能否为等腰三角形?如果能,请求出AE的长;如果不能,请说明理由.
23、已知反比例函数图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3, 若直线y=ax+b经过点A,并且经过反比例函数的图象上另一点C(n,—),
(1)反比例函数的解析式为?????????,m= ????,n= ??;
(2)求直线y=ax+b的解析式;
(3)在y轴上是否存在一点P,使△PAO为等腰三角形,若存在,请直接写出P点坐标,若不存在,说明理由。
24、如图,A、B两点在函数的图象上.
(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的坐标.
参考答案
一、填空题
1、m<2????????
2、????
3、6
4、(-2,0)或(-6,0)
5、(4,0)
6、2
二、选择题
7、B;8、B;9、C;10、C;11、C;12、A;13、D;14、C;15、D、;16、A.;17、D;18、B;
三、简答题
19、(1)??? (2)3
20、解:依题意得,反比例函数的解析式为的图像上。
因为点A(m,3)在反比例函数的图象上,
所以m=-1。
即点A的坐标为(-1,3)。
由点A(-1,3)在直线y=ax+2上,
可求得a=-1。
21、解:(1)反比例解析式:
??? ????一次函数:
?? ?(2)或
22、(1)当△BEF是等边三角形时,∠ABE=30°.
∵AB=12,∴AE=.
∴BF=BE=.
(2)作EG⊥BF,垂足为点G.
根据题意,得EG=AB=12,FG=y-x,EF=y.
∴.
∴所求的函数解析式为.
(3)∵∠AEB=∠FBE=∠FEB,∴点落在EF上.
∴,∠=∠=∠A=90°.
∴要使△成为等腰三角形,必须使.
而,,
∴.
∴.整理,得.
解得.
经检验:都原方程的根,但不符合题意,舍去.
当AE=时,△为等腰三角形.
23、(1);m=3; n=4….……3分(2)…………6分
?????? (3)答:存在点P使△PAO为等腰三角形;
点P坐标分别为:
P1(0,) ; P2(0,6);? P3(0,) ; ?P4(0,) ……10分
24、解:(1)由图象可知,函数的图象经过点A(1,6)
可得.
设直线的解析式为.
∵,两点在函数的图象上,
∴ 解得
∴直线的解析式为.
?
?
(2)图中阴影部分(不包括边界)所含格点的是(2,4) (3,3) (4,2)
