人教版七年级数学下册 5.4 平移教案
文档属性
| 名称 | 人教版七年级数学下册 5.4 平移教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 513.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 10:43:43 | ||
图片预览




文档简介
5.4 平移
课题
5.4 平移
授课人
教
学
目
标
知识技能
1.了解平移的特征,能发现某些特殊图案是可以通过平移得到的;
2.能发现、归纳图形平移的特征.
数学思考
通过讨论、探究、交流等形式,使学生在辩论中获得知识体验.
问题解决
经历操作、探究、归纳、总结图形平移的基本特征的过程,培养学生的抽象概括能力.
情感态度
学生经历操作、试验、发现、确认等数学活动,感受数学活动充满了探索性与创造性,激发学生勇于探究的热情.
教学
重点
图形平移的特征.
教学
难点
认识图形平移的特征.
授课
类型
新授课
课时
教具
多媒体,自制教具.
教学活动
教学
步骤
师生活动
设计意图
活动
一:
创设
情境
导入
新课
【课堂引入】
欣赏下面的图案.
图5-4-7
观察上面的图案,它们有什么相同的特点?能否根据其中的一部分绘制出整个图案?
培养学生的观察能力,使学生能通过观察确定基本图形.
活动
二:
实践
探究
交流
新知
【探究1】 平移的概念和性质
1.学生描图操作,教师根据学生情况进行如下指导.
(1)提出问题:如何在一张半透明的纸上,画出一排形状大小如的雪人?
(2)描图前教师说明:为了保证“按同一方向平移”,大家应该在雪人帽顶的上方约1厘米处画一条与书右边缘垂直的直线,半透明纸也应画一条直线,画图时要始终保持两条直线重合.
(3)学生描图,描出三个雪人图.
2.观察、思考.
(1)学生在自己所画出的相邻两个雪人中,找出三组对应点:鼻尖A与A',帽顶B与B',纽扣C与C',连接这些对应点.
(2)观察这些线段,它们的位置关系如何?数量关系呢?
学生用平移三角尺的方法验证三条线段是否平行,用刻度尺度量法确定三条线段是否相等.
教师在黑板上板书学生的发现:
AA'∥BB'∥CC',且AA'=BB'=CC'.
(3)学生再连接一些其他对应点的线段,验证前面的发现是否正确.
3.师生归纳
(1)描图起什么作用?
描出的图形与原来图形的形状、大小完全相同.在半透明纸上描出的所有雪人形状、大小完全相同.
1.教师指导学生如何准确画出图形.
2.观察图形中对应点间的位置关系与数量关系,归纳平移的概念.
活动
二:
实践
探究
交流
新知
(2)在书上和半透明纸上画直线而且要求描图时,两条直线要重合.这样做起什么作用?
保证在半透明纸上所画的图形沿直线所规定的方向移动.
(3)就半透明纸所画的图形归纳平移的性质
①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;
②新图形中的每一个点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
4.平移的定义.
定义:一个图形沿着某个方向移动一定的距离,图形的这种移动,叫做平移.
(1)让学生根据图5-4-8说明这些图形如何通过平移完成.
图5-4-8
(2)让学生根据图5-4-9说明图形是如何通过平移完成的.由此引导学生得出平移的方向不仅限于是水平的.
图5-4-9
(3)由学生举出生活中利用了平移的例子,如人在观光电梯上两个不同时刻之间的位置关系,坐登山缆车时人在吊箱里两个不同时刻的位置关系都是平移;黑板报中花边的设计利用的是平移;奥运会五环旗图案五环之间可通过平移得到……
3.注意方法的多样性,能答出平移结果都应当鼓励,但最后应当找出最基本的图形.
活动
三:
开放
训练
体现
应用
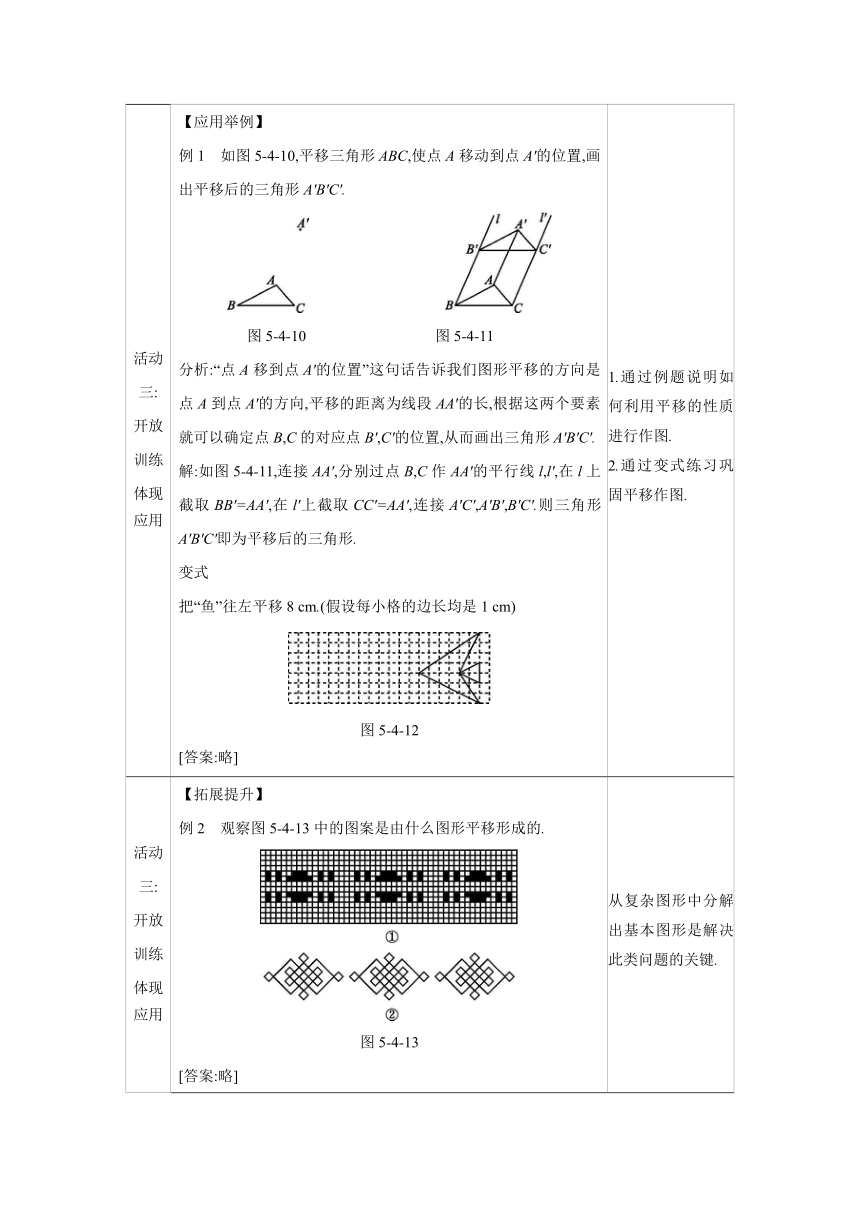
【应用举例】
例1 如图5-4-10,平移三角形ABC,使点A移动到点A'的位置,画出平移后的三角形A'B'C'.
图5-4-10 图5-4-11
分析:“点A移到点A'的位置”这句话告诉我们图形平移的方向是点A到点A'的方向,平移的距离为线段AA'的长,根据这两个要素就可以确定点B,C的对应点B',C'的位置,从而画出三角形A'B'C'.
解:如图5-4-11,连接AA',分别过点B,C作AA'的平行线l,l',在l上截取BB'=AA',在l'上截取CC'=AA',连接A'C',A'B',B'C'.则三角形A'B'C'即为平移后的三角形.
变式
把“鱼”往左平移8 cm.(假设每小格的边长均是1 cm)
图5-4-12
[答案:略]
1.通过例题说明如何利用平移的性质进行作图.
2.通过变式练习巩固平移作图.
活动
三:
开放
训练
体现
应用
【拓展提升】
例2 观察图5-4-13中的图案是由什么图形平移形成的.
图5-4-13
[答案:略]
从复杂图形中分解出基本图形是解决此类问题的关键.
活动
四:
课堂
总结
反思
【当堂训练】
1.图形经过平移后,图形的位置 改变 ,图形的形状 不改变 ,图形的大小 不改变 .(填“改变”或“不改变”)?
2.经过平移,每一组对应点所连成的线段 平行(或在同一条直线上)且相等 .?
3.如图5-4-14,线段CD是由线段AB平移后得到的图形,点C为点A的对应点,画出点B的对应点D的位置.
图5-4-14
课后作业:
课本第30页习题5.4第1,2,3,4,5题.
通过练习进一步加强对平移知识的理解和掌握.
【板书设计】
5.4 平移
框架图式总结,更容易形成知识网络.
【教学反思】
①[授课流程反思]
由比较美观的图形导入,既引起了学生的探究兴趣,又训练了学生的观察能力,使学生通过观察确定基本图形,引出平移的概念.
②[讲授效果反思]
本节课的教学效果较好,通过本节课的学习,学生由实例认识平移,理解平移的含义,理解平移前后两个图形对应点连线平行(或在同一条直线上)且相等,对应角相等,能够利用平移的性质进行平移作图.
回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师教学能力.
活动
四:
课堂
总结
反思
③[师生互动反思]
④[习题反思]
好题题号 ?
错题题号 ?
学习目标: 了解平移的概念,会进行点的平移,理解平移的性质,能解决简单的平移问题
重点:平移的概念和作图方法.
难点:平移的作图.
一预习导学
预习课本P28—P30,并完成以下练习
1、观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?
2如何在一张半透明的纸上,画出一排形状和大小如图的雪人?
2、在平面内,将一个图形沿某个方向___一定的距离,这样的图形运动称为平移,平移改变的是图形的_____。平移不改变图形的____和____。
3、图形的平移是由_____和_____决定的。
4、经过平移所得的图形与原来的图形的对应
线段_______,对应角____,对
应点所连的线段____。
5、如图1,△ABC平移到△DEF,图中相等的线段有_____________,相等的角有____________,平行的线段有______________。
6、把一个△ABC沿东南方向平移3cm,则AB边上的中点P沿___方向平移了__cm。
7、如图,△ABC是由四个形状大小相同的三角形拼成的,则可以看成是△ADF平移得到的小三角形是___________。
8、如图,△DEF是由△ABC先向右平移__格,再向___平移___格而得到的。
9、将正方形ABCD沿对角线AC方向平移,且平移后的图形的一个顶点恰好在AC的中点O处,则移动前后两个图形的重叠部分的面积是原正方形面积的____。
10、直角△ABC中,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为____cm2。
11、如图,有一条小船,若把小船平移,使点A平移到点B,请你在图中画出平移后的小船。
12、如图,平移三角形ABC,使点A运动到A`,画出平移后的三角形A`B`C`.
二、课堂学习研讨
(一)平移的概念
1、一个图形________________________叫做平移变换,简称平移。
2、下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
3、如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A.△OCD B.△OAB
C.△OAF D.△OEF
(二)平移的性质
1、平移后的图形与原图形_____、______完全相同,新图形中的每一个点,都是由___________________移动后得到的,这两个点是对应点,连接各组对应点的线段______且________或__________。对应线段______且________或__________。对应角_______。
2、如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A.AB∥DE且AB=DE B.∠DEC=∠B
C.AD∥EC且AD=EC D.BC=AD+EC
3、△ABC沿BC的方向平移到△DEF的位置,(1)若∠B=260,∠F=740,则∠1=_______,∠2=______,∠A=_______,∠D=______
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于________,DF=_______,CF=_________。
(三)平移作图
1、△ABC在网格中如图所示,请根据下列提示作图
(1)向上平移2个单位长度.
(2) 再向右移3个单位长度.
2、已知三角形ABC、点D,D为A的对应点。过点D作三角形ABC平移后的图形。
三、随堂小测
(一)选择题
1、下列哪个图形是由左图平移得到的( )
2、如图所示,△FDE经过怎样的平移可得到△ABC.( )
沿射线EC的方向移动DB长;
B.沿射线EC的方向移动CD长
沿射线BD的方向移动BD长;
D.沿射线BD的方向移动DC长
3、下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
4、如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分别是( )
A.∠F,AC B.∠BOD,BA
C.∠F,BA D.∠BOD,AC
5、在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等
(二)填空题
1、在平移过程中,平移后的图形与原来的图形________和_________都相同,因此对应线段和对应角都________.
2、如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=____度,∠EDF=_______度,∠F=______度,∠DOB=_______度.
(三)解答题
1、如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.
2、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置.
3、如图所示,画出平行四边形ABCD向上平移1厘米后的图形.
4、如图,将△ABC沿东北方向平移3cm。
5、完成下列推理过程:如图,已知AB∥CD,CD∥EF,∠A=105°,∠ACE=51°,求:∠E的度数.
解:∵AB∥CD(已知),
∴∠A+_____=180°( ).
∵∠A=105°( ),
∴∠ACD=180°-105°=_______.
∴∠DCE=∠ACD-∠ACE=75°-51°=______________,
又∵EF∥CD( ),
∴∠E=_______ =___
6、如图所示,己知∠1=∠2,
∠3=∠4,∠5=∠C,
求证:DE//BF
课题
5.4 平移
授课人
教
学
目
标
知识技能
1.了解平移的特征,能发现某些特殊图案是可以通过平移得到的;
2.能发现、归纳图形平移的特征.
数学思考
通过讨论、探究、交流等形式,使学生在辩论中获得知识体验.
问题解决
经历操作、探究、归纳、总结图形平移的基本特征的过程,培养学生的抽象概括能力.
情感态度
学生经历操作、试验、发现、确认等数学活动,感受数学活动充满了探索性与创造性,激发学生勇于探究的热情.
教学
重点
图形平移的特征.
教学
难点
认识图形平移的特征.
授课
类型
新授课
课时
教具
多媒体,自制教具.
教学活动
教学
步骤
师生活动
设计意图
活动
一:
创设
情境
导入
新课
【课堂引入】
欣赏下面的图案.
图5-4-7
观察上面的图案,它们有什么相同的特点?能否根据其中的一部分绘制出整个图案?
培养学生的观察能力,使学生能通过观察确定基本图形.
活动
二:
实践
探究
交流
新知
【探究1】 平移的概念和性质
1.学生描图操作,教师根据学生情况进行如下指导.
(1)提出问题:如何在一张半透明的纸上,画出一排形状大小如的雪人?
(2)描图前教师说明:为了保证“按同一方向平移”,大家应该在雪人帽顶的上方约1厘米处画一条与书右边缘垂直的直线,半透明纸也应画一条直线,画图时要始终保持两条直线重合.
(3)学生描图,描出三个雪人图.
2.观察、思考.
(1)学生在自己所画出的相邻两个雪人中,找出三组对应点:鼻尖A与A',帽顶B与B',纽扣C与C',连接这些对应点.
(2)观察这些线段,它们的位置关系如何?数量关系呢?
学生用平移三角尺的方法验证三条线段是否平行,用刻度尺度量法确定三条线段是否相等.
教师在黑板上板书学生的发现:
AA'∥BB'∥CC',且AA'=BB'=CC'.
(3)学生再连接一些其他对应点的线段,验证前面的发现是否正确.
3.师生归纳
(1)描图起什么作用?
描出的图形与原来图形的形状、大小完全相同.在半透明纸上描出的所有雪人形状、大小完全相同.
1.教师指导学生如何准确画出图形.
2.观察图形中对应点间的位置关系与数量关系,归纳平移的概念.
活动
二:
实践
探究
交流
新知
(2)在书上和半透明纸上画直线而且要求描图时,两条直线要重合.这样做起什么作用?
保证在半透明纸上所画的图形沿直线所规定的方向移动.
(3)就半透明纸所画的图形归纳平移的性质
①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;
②新图形中的每一个点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行(或在同一条直线上)且相等.
4.平移的定义.
定义:一个图形沿着某个方向移动一定的距离,图形的这种移动,叫做平移.
(1)让学生根据图5-4-8说明这些图形如何通过平移完成.
图5-4-8
(2)让学生根据图5-4-9说明图形是如何通过平移完成的.由此引导学生得出平移的方向不仅限于是水平的.
图5-4-9
(3)由学生举出生活中利用了平移的例子,如人在观光电梯上两个不同时刻之间的位置关系,坐登山缆车时人在吊箱里两个不同时刻的位置关系都是平移;黑板报中花边的设计利用的是平移;奥运会五环旗图案五环之间可通过平移得到……
3.注意方法的多样性,能答出平移结果都应当鼓励,但最后应当找出最基本的图形.
活动
三:
开放
训练
体现
应用
【应用举例】
例1 如图5-4-10,平移三角形ABC,使点A移动到点A'的位置,画出平移后的三角形A'B'C'.
图5-4-10 图5-4-11
分析:“点A移到点A'的位置”这句话告诉我们图形平移的方向是点A到点A'的方向,平移的距离为线段AA'的长,根据这两个要素就可以确定点B,C的对应点B',C'的位置,从而画出三角形A'B'C'.
解:如图5-4-11,连接AA',分别过点B,C作AA'的平行线l,l',在l上截取BB'=AA',在l'上截取CC'=AA',连接A'C',A'B',B'C'.则三角形A'B'C'即为平移后的三角形.
变式
把“鱼”往左平移8 cm.(假设每小格的边长均是1 cm)
图5-4-12
[答案:略]
1.通过例题说明如何利用平移的性质进行作图.
2.通过变式练习巩固平移作图.
活动
三:
开放
训练
体现
应用
【拓展提升】
例2 观察图5-4-13中的图案是由什么图形平移形成的.
图5-4-13
[答案:略]
从复杂图形中分解出基本图形是解决此类问题的关键.
活动
四:
课堂
总结
反思
【当堂训练】
1.图形经过平移后,图形的位置 改变 ,图形的形状 不改变 ,图形的大小 不改变 .(填“改变”或“不改变”)?
2.经过平移,每一组对应点所连成的线段 平行(或在同一条直线上)且相等 .?
3.如图5-4-14,线段CD是由线段AB平移后得到的图形,点C为点A的对应点,画出点B的对应点D的位置.
图5-4-14
课后作业:
课本第30页习题5.4第1,2,3,4,5题.
通过练习进一步加强对平移知识的理解和掌握.
【板书设计】
5.4 平移
框架图式总结,更容易形成知识网络.
【教学反思】
①[授课流程反思]
由比较美观的图形导入,既引起了学生的探究兴趣,又训练了学生的观察能力,使学生通过观察确定基本图形,引出平移的概念.
②[讲授效果反思]
本节课的教学效果较好,通过本节课的学习,学生由实例认识平移,理解平移的含义,理解平移前后两个图形对应点连线平行(或在同一条直线上)且相等,对应角相等,能够利用平移的性质进行平移作图.
回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师教学能力.
活动
四:
课堂
总结
反思
③[师生互动反思]
④[习题反思]
好题题号 ?
错题题号 ?
学习目标: 了解平移的概念,会进行点的平移,理解平移的性质,能解决简单的平移问题
重点:平移的概念和作图方法.
难点:平移的作图.
一预习导学
预习课本P28—P30,并完成以下练习
1、观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?
2如何在一张半透明的纸上,画出一排形状和大小如图的雪人?
2、在平面内,将一个图形沿某个方向___一定的距离,这样的图形运动称为平移,平移改变的是图形的_____。平移不改变图形的____和____。
3、图形的平移是由_____和_____决定的。
4、经过平移所得的图形与原来的图形的对应
线段_______,对应角____,对
应点所连的线段____。
5、如图1,△ABC平移到△DEF,图中相等的线段有_____________,相等的角有____________,平行的线段有______________。
6、把一个△ABC沿东南方向平移3cm,则AB边上的中点P沿___方向平移了__cm。
7、如图,△ABC是由四个形状大小相同的三角形拼成的,则可以看成是△ADF平移得到的小三角形是___________。
8、如图,△DEF是由△ABC先向右平移__格,再向___平移___格而得到的。
9、将正方形ABCD沿对角线AC方向平移,且平移后的图形的一个顶点恰好在AC的中点O处,则移动前后两个图形的重叠部分的面积是原正方形面积的____。
10、直角△ABC中,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为____cm2。
11、如图,有一条小船,若把小船平移,使点A平移到点B,请你在图中画出平移后的小船。
12、如图,平移三角形ABC,使点A运动到A`,画出平移后的三角形A`B`C`.
二、课堂学习研讨
(一)平移的概念
1、一个图形________________________叫做平移变换,简称平移。
2、下列各组图形中,可以经过平移变换由一个图形得到另一个图形的是( )
3、如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( )
A.△OCD B.△OAB
C.△OAF D.△OEF
(二)平移的性质
1、平移后的图形与原图形_____、______完全相同,新图形中的每一个点,都是由___________________移动后得到的,这两个点是对应点,连接各组对应点的线段______且________或__________。对应线段______且________或__________。对应角_______。
2、如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
A.AB∥DE且AB=DE B.∠DEC=∠B
C.AD∥EC且AD=EC D.BC=AD+EC
3、△ABC沿BC的方向平移到△DEF的位置,(1)若∠B=260,∠F=740,则∠1=_______,∠2=______,∠A=_______,∠D=______
(2)若AB=4cm,AC=5cm,BC=4.5cm,EC=3.5cm,则平移的距离等于________,DF=_______,CF=_________。
(三)平移作图
1、△ABC在网格中如图所示,请根据下列提示作图
(1)向上平移2个单位长度.
(2) 再向右移3个单位长度.
2、已知三角形ABC、点D,D为A的对应点。过点D作三角形ABC平移后的图形。
三、随堂小测
(一)选择题
1、下列哪个图形是由左图平移得到的( )
2、如图所示,△FDE经过怎样的平移可得到△ABC.( )
沿射线EC的方向移动DB长;
B.沿射线EC的方向移动CD长
沿射线BD的方向移动BD长;
D.沿射线BD的方向移动DC长
3、下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
4、如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分别是( )
A.∠F,AC B.∠BOD,BA
C.∠F,BA D.∠BOD,AC
5、在平移过程中,对应线段( )
A.互相平行且相等; B.互相垂直且相等 C.互相平行(或在同一条直线上)且相等
(二)填空题
1、在平移过程中,平移后的图形与原来的图形________和_________都相同,因此对应线段和对应角都________.
2、如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=____度,∠EDF=_______度,∠F=______度,∠DOB=_______度.
(三)解答题
1、如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.
2、如图所示,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置.
3、如图所示,画出平行四边形ABCD向上平移1厘米后的图形.
4、如图,将△ABC沿东北方向平移3cm。
5、完成下列推理过程:如图,已知AB∥CD,CD∥EF,∠A=105°,∠ACE=51°,求:∠E的度数.
解:∵AB∥CD(已知),
∴∠A+_____=180°( ).
∵∠A=105°( ),
∴∠ACD=180°-105°=_______.
∴∠DCE=∠ACD-∠ACE=75°-51°=______________,
又∵EF∥CD( ),
∴∠E=_______ =___
6、如图所示,己知∠1=∠2,
∠3=∠4,∠5=∠C,
求证:DE//BF
