人教版八年级数学下册17.1.1勾股定理课件 (共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1.1勾股定理课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览

文档简介
(共21张PPT)
☆新人教版☆八年级下册☆
◇第十七章◇勾股定理◇
☆17.1.3☆勾股定理(3)☆
◇十一崇仁◇ 方世超 ◇
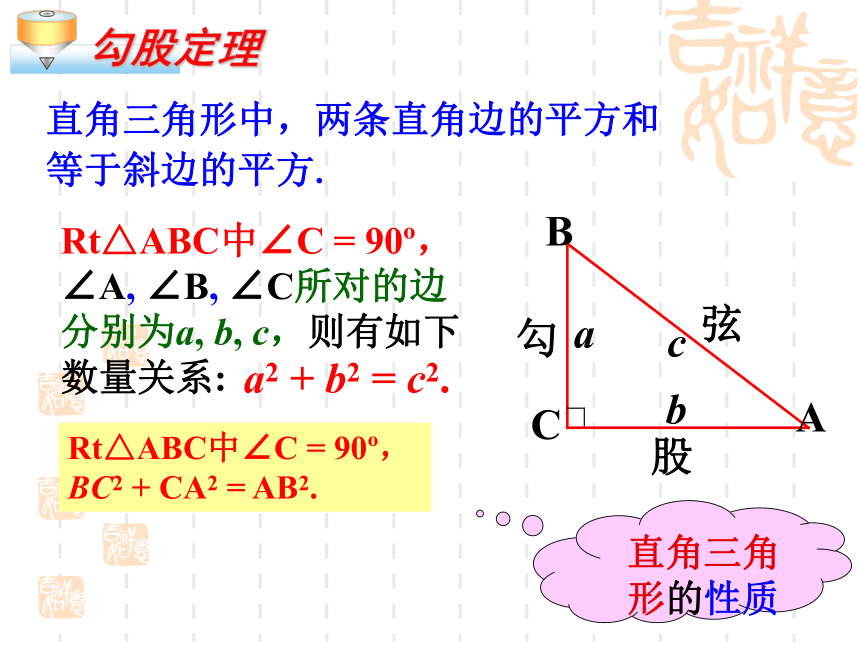
Rt△ABC中∠C = 90?,∠A, ∠B, ∠C所对的边分别为a, b, c,则有如下数量关系:
直角三角形中,两条直角边的平方和等于斜边的平方.
a2 + b2 = c2.
勾
股
弦
Rt△ABC中∠C = 90?,BC2 + CA2 = AB2.
直角三角形的性质
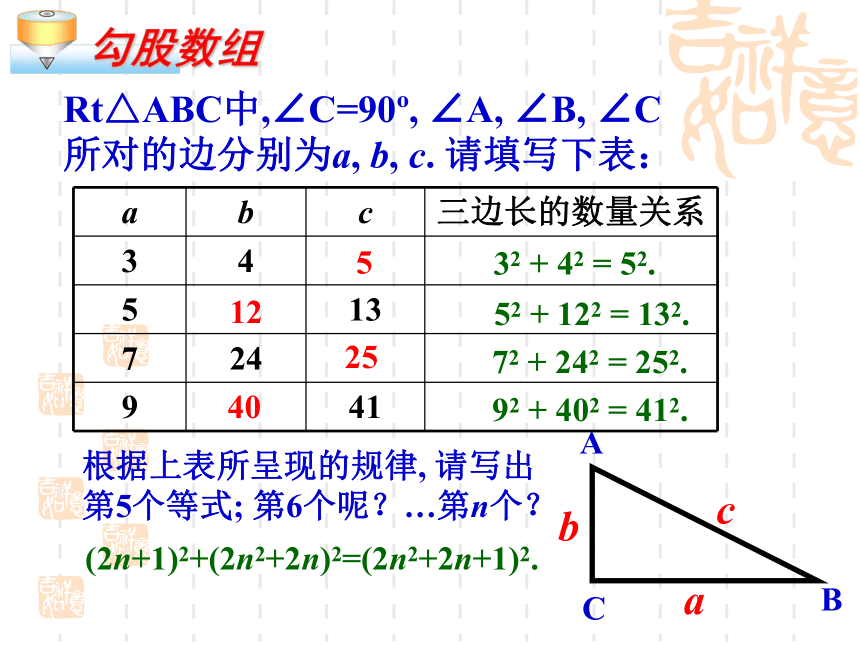
Rt△ABC中,∠C=90?, ∠A, ∠B, ∠C所对的边分别为a, b, c. 请填写下表:
根据上表所呈现的规律, 请写出第5个等式; 第6个呢?…第n个?
5
32 + 42 = 52.
12
52 + 122 = 132.
25
72 + 242 = 252.
40
92 + 402 = 412.
(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
a b c 三边长的数量关系
3 4
5 13
7 24
9 41
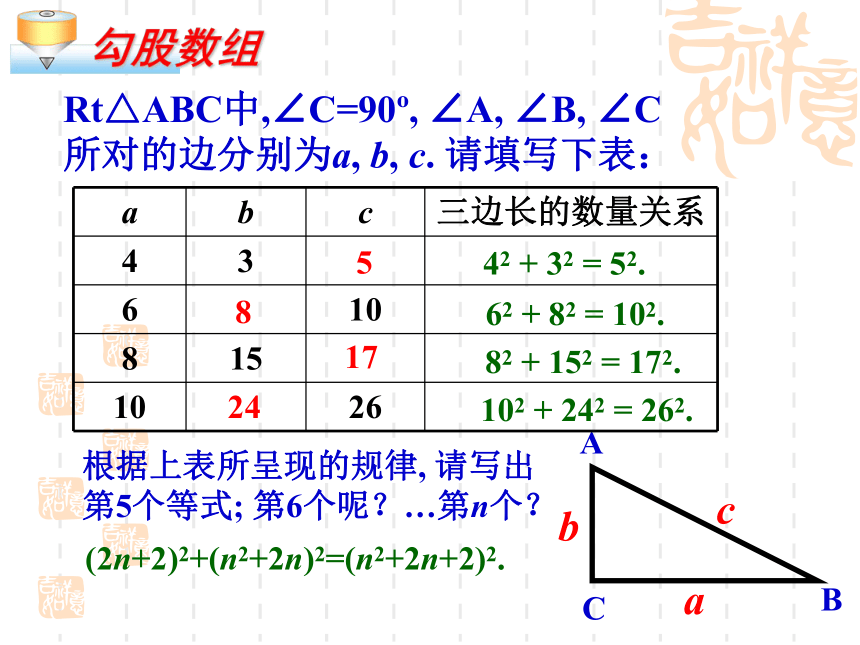
Rt△ABC中,∠C=90?, ∠A, ∠B, ∠C所对的边分别为a, b, c. 请填写下表:
根据上表所呈现的规律, 请写出第5个等式; 第6个呢?…第n个?
5
42 + 32 = 52.
8
62 + 82 = 102.
17
82 + 152 = 172.
24
102 + 242 = 262.
(2n+2)2+(n2+2n)2=(n2+2n+2)2.
a b c 三边长的数量关系
4 3
6 10
8 15
10 26
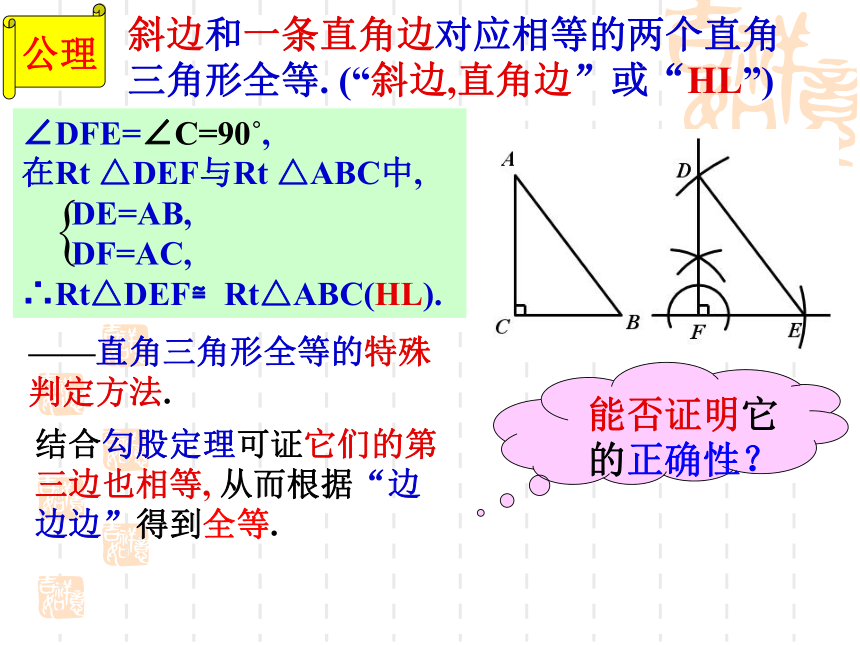
斜边和一条直角边对应相等的两个直角三角形全等. (“斜边,直角边”或“HL”)
——直角三角形全等的特殊判定方法.
∠DFE=∠C=90?,
在Rt △DEF与Rt △ABC中,
DE=AB,
DF=AC,
∴Rt△DEF≌Rt△ABC(HL).
能否证明它的正确性?
结合勾股定理可证它们的第三边也相等, 从而根据“边边边”得到全等.
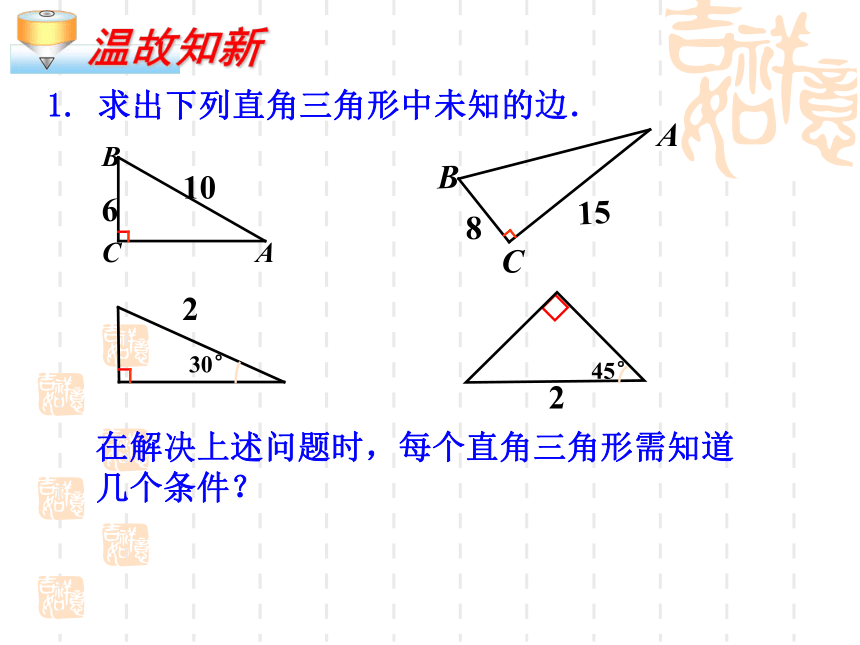
1. 求出下列直角三角形中未知的边.
在解决上述问题时,每个直角三角形需知道几个条件?
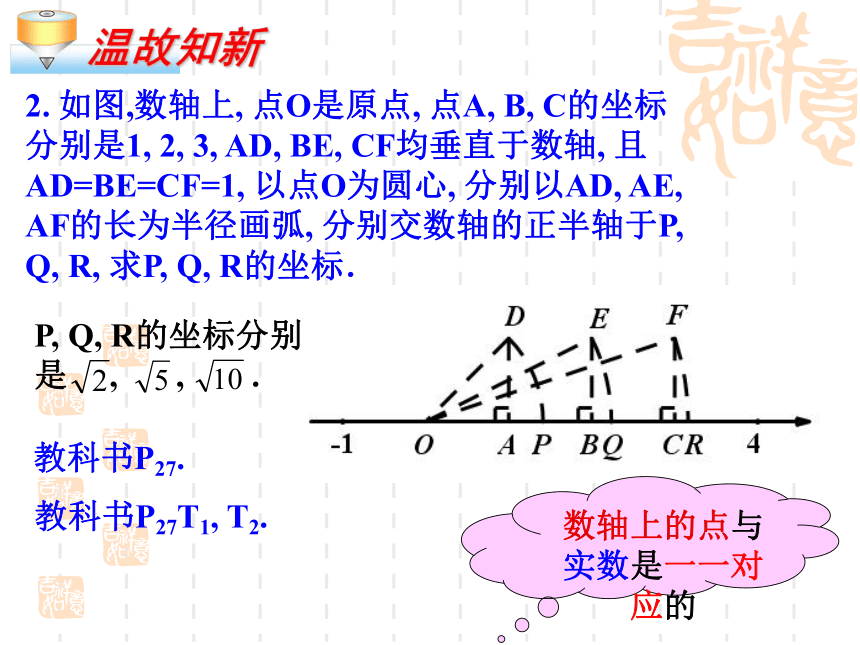
2. 如图,数轴上, 点O是原点, 点A, B, C的坐标分别是1, 2, 3, AD, BE, CF均垂直于数轴, 且AD=BE=CF=1, 以点O为圆心, 分别以AD, AE, AF的长为半径画弧, 分别交数轴的正半轴于P, Q, R, 求P, Q, R的坐标.
数轴上的点与实数是一一对应的
P, Q, R的坐标分别
是 , , .
教科书P27.
教科书P27T1, T2.
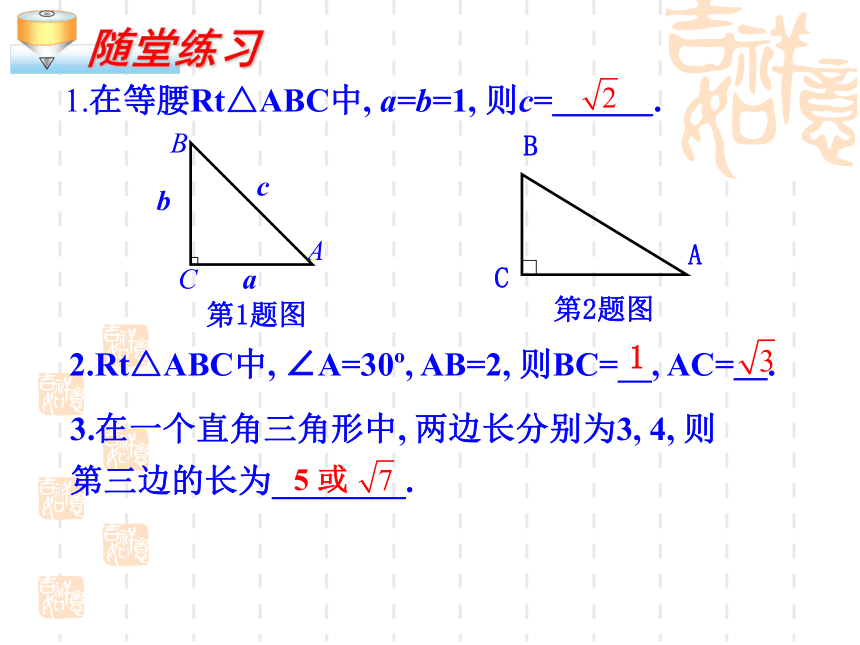
1.在等腰Rt△ABC中, a=b=1, 则c=___.
第1题图
第2题图
3.在一个直角三角形中, 两边长分别为3, 4, 则第三边的长为________.
5 或
2.Rt△ABC中, ∠A=30?, AB=2, 则BC=__, AC=_.
1
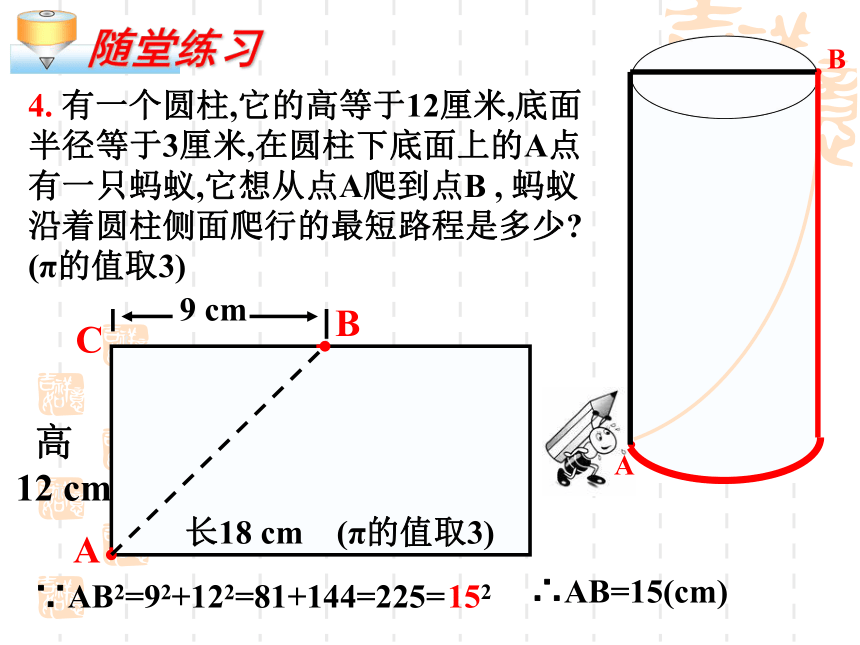
4. 有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)
A
B
C
长18 cm (π的值取3)
高
12 cm
∵AB2=92+122=81+144=225=
152
∴AB=15(cm)
5. 在一个内腔长30 cm, 宽40 cm, 高50 cm的木箱中放一根笔直的细玻璃管, 这根玻璃管的长度至多为多少cm?
A
C
B
D
Rt△ACD中∠ADC=90?,
AC2=AD2+CD2=402+302
=502,
Rt△ACB中∠ACB=90?,
AB2=AC2+BC2
=402+302+502
=502×2,
∴AB=50 cm.
6. 如图, 已知:等腰直角△ABC中, P为斜边BC上的任一点. 求证:PB2+PC2=2PA2 .
D
7.(广东·中考)如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));……以此下去,则正方形A4B4C4D4的面积为__________.
图(1)
A1
B1
C1
D1
A
B
C
D
D2
A2
B2
C2
D1
C1
B1
A1
A
B
C
D
图(2)
【解析】由勾股定理得:新正方形A1B1C1D1边长为 ,正
方形A2B2C2D2边长为5,···,正方形A4B4C4D4的边长为25,
正方形A4B4C4D4的面积为625.
答案:625
8.矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长.
A
B
C
D
F
E
解:设DE为x,
X
(8- X)
则CE为 (8-x).
由题意可知:EF=DE=x,
X
AF=AD=10.
10
10
8
∵∠B=90°,
∴ AB2+ BF2=AF2,
即82+ BF2=102,
∴BF=6,
∴CF=BC-BF=10-6=4.
∵∠C=90°,
∴ CE2+CF2=EF2,
(8-x)2+42=x2,
64-16x+x2+16=x2,
80 -16x=0,
16x=80
x=5
在Rt△ADE中∠D=90°,
∴AE2=AD2+DE2,
∴AE2=102+52=125,
∴AE=
9. 如图,棱长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
A.3 B. C.2 D.1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
1.在Rt△ABC中,∠C=90°,
已知: a=5, b=12, 求c.
已知: b=6,c=10 , 求a.
已知: a=7, c=25, 求b.
2.一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.
4.一架长为5的梯子,斜立靠在一竖直的墙上,这时梯子下端距离墙的底端为3,若梯子顶端下滑了1,则梯子底端将外移_____.
5.如图,要在高为3m,斜坡为5m的楼梯表
面铺地毯,地毯的长度至少需________m
6.把直角三角形两条直角边同时扩大到原来
的3倍,则其斜边( )
A.不变 B.扩大到原来的3倍
C.扩大到原来的9倍 D.减小到原来的1/3
A
B
C
1
7
B
7.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高____________米。
15
8.小东拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少米?
解:设竹竿长x米,则城门高为 (x-1)米.
根据题意得:
32+ (x-1) 2 =x2
9+x2-2x+1=x2
10 -2x=0
2x=10
x=5
答:竹竿长5米.
理想是指路明灯.没有理想,就没有坚定的方向,而没有方向,就没有生活.
—— 托尔斯泰
☆新人教版☆八年级下册☆
◇第十七章◇勾股定理◇
☆17.1.3☆勾股定理(3)☆
◇十一崇仁◇ 方世超 ◇
Rt△ABC中∠C = 90?,∠A, ∠B, ∠C所对的边分别为a, b, c,则有如下数量关系:
直角三角形中,两条直角边的平方和等于斜边的平方.
a2 + b2 = c2.
勾
股
弦
Rt△ABC中∠C = 90?,BC2 + CA2 = AB2.
直角三角形的性质
Rt△ABC中,∠C=90?, ∠A, ∠B, ∠C所对的边分别为a, b, c. 请填写下表:
根据上表所呈现的规律, 请写出第5个等式; 第6个呢?…第n个?
5
32 + 42 = 52.
12
52 + 122 = 132.
25
72 + 242 = 252.
40
92 + 402 = 412.
(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
a b c 三边长的数量关系
3 4
5 13
7 24
9 41
Rt△ABC中,∠C=90?, ∠A, ∠B, ∠C所对的边分别为a, b, c. 请填写下表:
根据上表所呈现的规律, 请写出第5个等式; 第6个呢?…第n个?
5
42 + 32 = 52.
8
62 + 82 = 102.
17
82 + 152 = 172.
24
102 + 242 = 262.
(2n+2)2+(n2+2n)2=(n2+2n+2)2.
a b c 三边长的数量关系
4 3
6 10
8 15
10 26
斜边和一条直角边对应相等的两个直角三角形全等. (“斜边,直角边”或“HL”)
——直角三角形全等的特殊判定方法.
∠DFE=∠C=90?,
在Rt △DEF与Rt △ABC中,
DE=AB,
DF=AC,
∴Rt△DEF≌Rt△ABC(HL).
能否证明它的正确性?
结合勾股定理可证它们的第三边也相等, 从而根据“边边边”得到全等.
1. 求出下列直角三角形中未知的边.
在解决上述问题时,每个直角三角形需知道几个条件?
2. 如图,数轴上, 点O是原点, 点A, B, C的坐标分别是1, 2, 3, AD, BE, CF均垂直于数轴, 且AD=BE=CF=1, 以点O为圆心, 分别以AD, AE, AF的长为半径画弧, 分别交数轴的正半轴于P, Q, R, 求P, Q, R的坐标.
数轴上的点与实数是一一对应的
P, Q, R的坐标分别
是 , , .
教科书P27.
教科书P27T1, T2.
1.在等腰Rt△ABC中, a=b=1, 则c=___.
第1题图
第2题图
3.在一个直角三角形中, 两边长分别为3, 4, 则第三边的长为________.
5 或
2.Rt△ABC中, ∠A=30?, AB=2, 则BC=__, AC=_.
1
4. 有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B , 蚂蚁沿着圆柱侧面爬行的最短路程是多少? (π的值取3)
A
B
C
长18 cm (π的值取3)
高
12 cm
∵AB2=92+122=81+144=225=
152
∴AB=15(cm)
5. 在一个内腔长30 cm, 宽40 cm, 高50 cm的木箱中放一根笔直的细玻璃管, 这根玻璃管的长度至多为多少cm?
A
C
B
D
Rt△ACD中∠ADC=90?,
AC2=AD2+CD2=402+302
=502,
Rt△ACB中∠ACB=90?,
AB2=AC2+BC2
=402+302+502
=502×2,
∴AB=50 cm.
6. 如图, 已知:等腰直角△ABC中, P为斜边BC上的任一点. 求证:PB2+PC2=2PA2 .
D
7.(广东·中考)如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));……以此下去,则正方形A4B4C4D4的面积为__________.
图(1)
A1
B1
C1
D1
A
B
C
D
D2
A2
B2
C2
D1
C1
B1
A1
A
B
C
D
图(2)
【解析】由勾股定理得:新正方形A1B1C1D1边长为 ,正
方形A2B2C2D2边长为5,···,正方形A4B4C4D4的边长为25,
正方形A4B4C4D4的面积为625.
答案:625
8.矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长.
A
B
C
D
F
E
解:设DE为x,
X
(8- X)
则CE为 (8-x).
由题意可知:EF=DE=x,
X
AF=AD=10.
10
10
8
∵∠B=90°,
∴ AB2+ BF2=AF2,
即82+ BF2=102,
∴BF=6,
∴CF=BC-BF=10-6=4.
∵∠C=90°,
∴ CE2+CF2=EF2,
(8-x)2+42=x2,
64-16x+x2+16=x2,
80 -16x=0,
16x=80
x=5
在Rt△ADE中∠D=90°,
∴AE2=AD2+DE2,
∴AE2=102+52=125,
∴AE=
9. 如图,棱长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
A.3 B. C.2 D.1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
1.在Rt△ABC中,∠C=90°,
已知: a=5, b=12, 求c.
已知: b=6,c=10 , 求a.
已知: a=7, c=25, 求b.
2.一直角三角形的一直角边长为7, 另两条边长为两个连续整数,求这个直角三角形的周长.
4.一架长为5的梯子,斜立靠在一竖直的墙上,这时梯子下端距离墙的底端为3,若梯子顶端下滑了1,则梯子底端将外移_____.
5.如图,要在高为3m,斜坡为5m的楼梯表
面铺地毯,地毯的长度至少需________m
6.把直角三角形两条直角边同时扩大到原来
的3倍,则其斜边( )
A.不变 B.扩大到原来的3倍
C.扩大到原来的9倍 D.减小到原来的1/3
A
B
C
1
7
B
7.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高____________米。
15
8.小东拿着一根长竹竿进一个宽为3米的城门,他先横着拿不进去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少米?
解:设竹竿长x米,则城门高为 (x-1)米.
根据题意得:
32+ (x-1) 2 =x2
9+x2-2x+1=x2
10 -2x=0
2x=10
x=5
答:竹竿长5米.
理想是指路明灯.没有理想,就没有坚定的方向,而没有方向,就没有生活.
—— 托尔斯泰
