人教版七年级下册 5.2 平行线及其判定 同步练习含答案
文档属性
| 名称 | 人教版七年级下册 5.2 平行线及其判定 同步练习含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览


文档简介
平行线及其判定 同步练习
1、选择题
1、在同一平面内,两条不重合直线的位置关系可能是(?? )。
A.?平行或相交?????????????B.?垂直或相交
C.?垂直或平行?????????????D.?平行、垂直或相交
2、下列说法中,正确的个数为(?? )
(1)过一点有无数条直线与已知直线平行
(2)如果a∥b,a∥c,那么b∥c
(3如果两线段不相交,那么它们就平行?? (4)如果两直线不相交,那么它们就平行
A.1个????? B.2个????? C.3个????? D.4个
3、如果∠α与∠β是对顶角且互补,则它们两边所在的直线( ).
A.互相垂直??????? B.互相平行????? C.即不垂直也不平行???? D.不能确定
4、如图1,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A. 同位角相等,两直线平行 B.内错角相等,两直线平行??
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
5、如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠4 ???B.∠D=∠DCE?? ?C.∠1=∠2?? ?D.∠D+∠ACD=180°
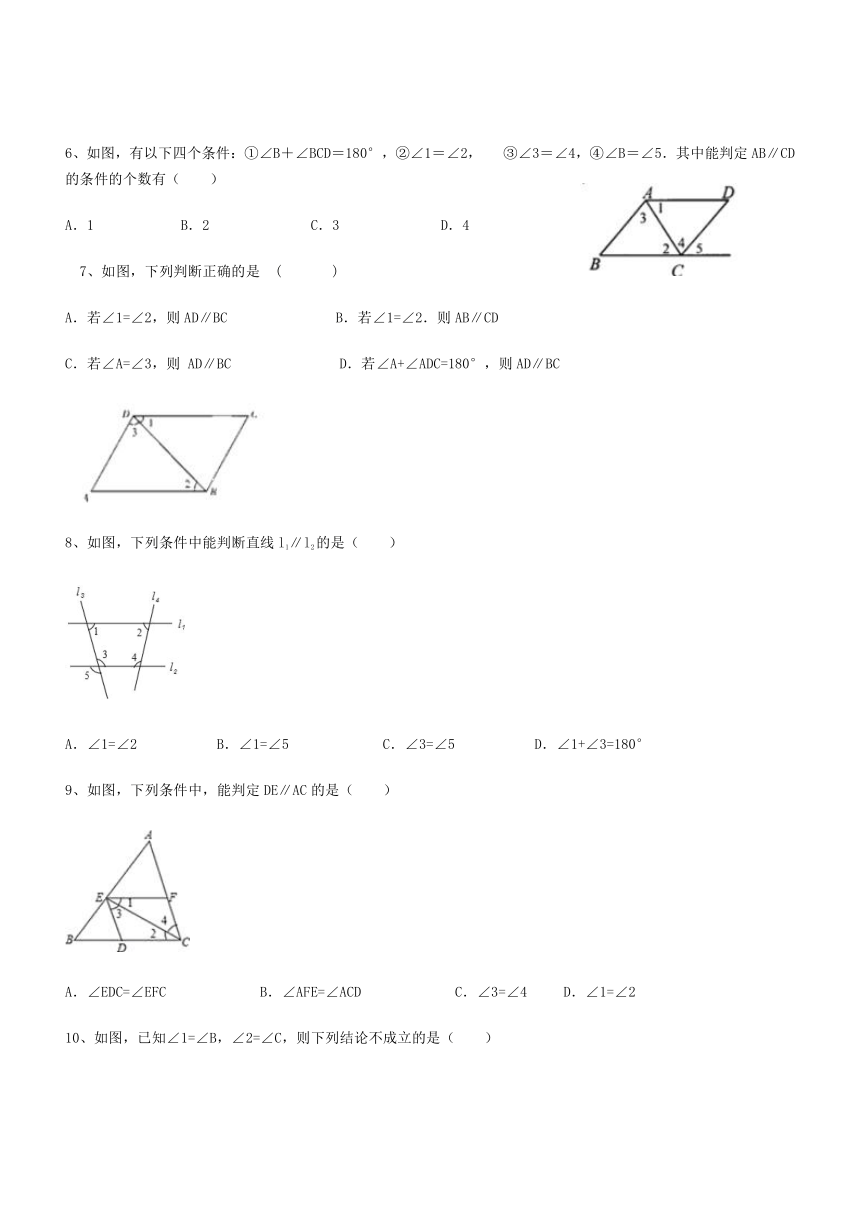
6、如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,? ③∠3=∠4,④∠B=∠5.其中能判定AB∥CD的条件的个数有(??)
A.1??? ?? B.2 ?????? C.3?? ??? ?D.4
?7、如图,下列判断正确的是?(??? )
A.若∠1=∠2,则AD∥BC??????? B.若∠1=∠2.则AB∥CD
C.若∠A=∠3,则 AD∥BC??????? D.若∠A+∠ADC=180°,则AD∥BC
8、如图,下列条件中能判断直线l1∥l2的是( )
A.∠1=∠2????? B.∠1=∠5?????? C.∠3=∠5????? D.∠1+∠3=180°
9、如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC?????? B.∠AFE=∠ACD?????? C.∠3=∠4?? D.∠1=∠2
10、如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( )???????????
????????????????????????????????????????
A.∠2+∠B=180°??? B.AD∥BC??????? C.AB=BC??????? D.AB∥CD
二、填空题
11、如图,已知∠A=75°,∠B=105°? 则?????∥?????.?
12、如上中图所示,∠1=∠2,则?????∥?????,∠BAD+?????=180°.
13、如图,装修工人向墙上钉木条.若∠2=100°,要使木条b与a平行,则∠1的度数等于?????? .
???? ???????????
14、长方形ABCD中,∠ADB=20°,现将这一长方形纸片沿AF折叠,若使AB′∥BD,则折痕AF与AB的夹角∠BAF应为?????
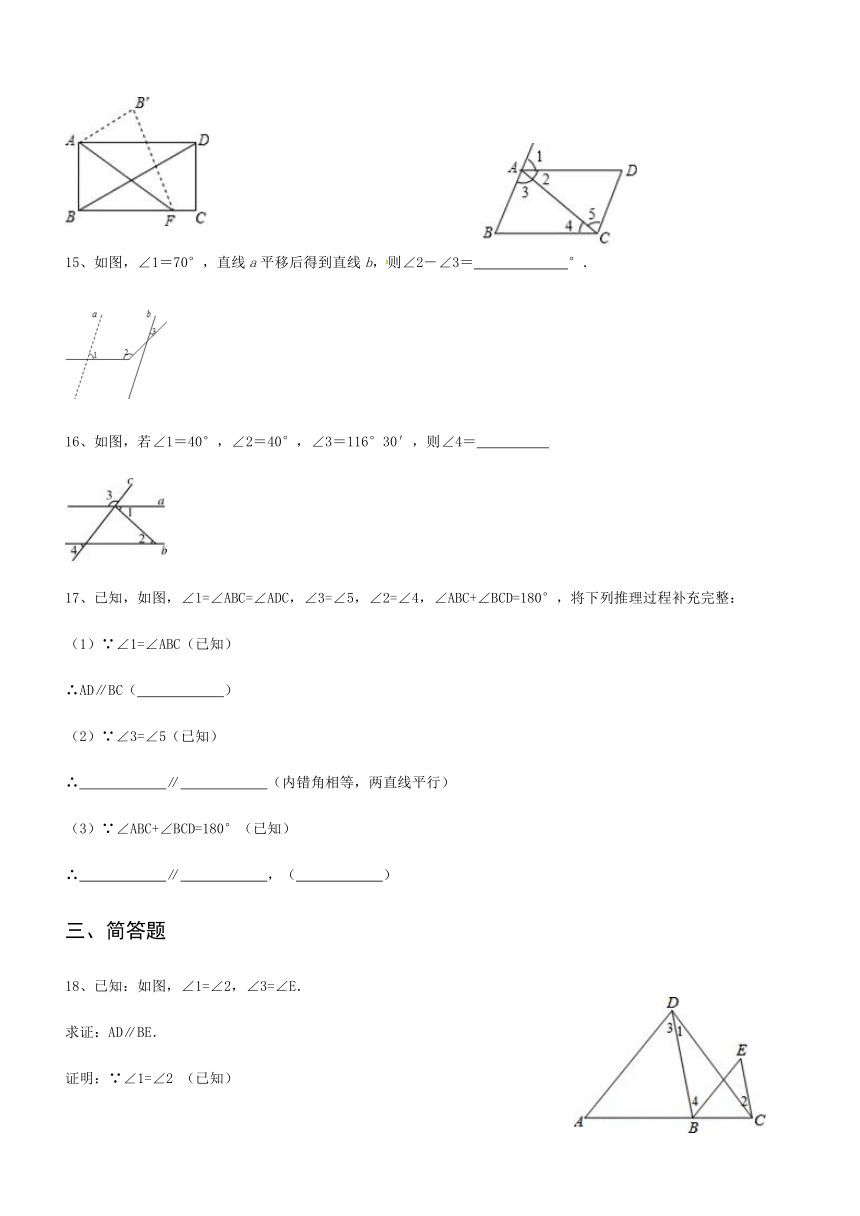
15、如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=?? ????°.
16、如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=?????
???????????
17、已知,如图,∠1=∠ABC=∠ADC,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°,将下列推理过程补充完整:
(1)∵∠1=∠ABC(已知)
∴AD∥BC( )
(2)∵∠3=∠5(已知)
∴ ∥ (内错角相等,两直线平行)
(3)∵∠ABC+∠BCD=180°(已知)
∴ ∥ ,( )
三、简答题
18、已知:如图,∠1=∠2,∠3=∠E.
求证:AD∥BE.
证明:∵∠1=∠2 (已知)
∴ ∥ ( ????????????????????? )
∴∠E=∠ ( ????????????????????? )?????????? ?
又∵∠E=∠3 ( 已知 )
∴∠3=∠ ( ????????? )
∴AD∥BE.( ?????????????????????? )
19、读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.????????
20、已知:如图,∠B=42°,∠A+10°=∠1,∠ACD=64°求证:AB∥CD。
21、.如图,AB∥CD,EF分别交AB、CD于点G、H,∠BGH、∠DHF的平分线分别为GM、HN.求证:GM∥HN.
??
22、已知:如图,∠1 =∠2,∠3 =∠4,∠5 =∠6.求证:ED ∥FB.
参考答案
一、选择题
1、A;2、A;3、A;;4、A;;5、C;6、C;;7、B;8、D;9、C;10、C;
二、填空题
11、AD∥BC?
12、AD? BC? ∠B
13、80
14、 55°
15、110??????
16、63°30′
17、(1))∵∠1=∠ABC(已知)
∴AD∥BC(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行;
(2)∵∠3=∠5,
∴AB∥CD(内错角相等,两直线平行).
故答案为:AB,CD;
(3))∵∠ABC+∠BCD=180°(已知)
∴AB∥CD,(同旁内角互补,两直线平行).
故答案为:AB,CD,同旁内角互补,两直线平行.
三、简答题
18、证明:∵∠1=∠2 (已知)
∴ DB ∥ EC ( 内错角相等,两直线平行???? )
∴∠E=∠ 4 ( ? 两直线平行,内错角相等??? )
又∵∠E=∠3 ( 已知 )
∴∠3=∠ 4 ( 等量代换???? )
∴AD∥BE.( ?? 内错角相等,两直线平行?? )
19、解:(1)(2)如图所示.
??????
(3)∠PQC=60°.
∵ PQ∥CD,
∴ ∠DCB+∠PQC=180°.
∵ ∠DCB=120°,
∴ ∠PQC=180°120°=60°.
20、解:因为∠B=42°,∠A+10°=∠1,又∠B+∠A+∠1=180°,所以∠A=64°,所以∠1=74°;
因为∠DCA+∠1+∠B=64°+74°+42°=180°,所以:AB∥CD。
21、
22、证明:∵ ∠3 =∠4,∴ AC∥BD.∴ ∠6+∠2+∠3 = 180°.
∵ ∠6 =∠5,∠2 =∠1,∴ ∠5+∠1+∠3 = 180°.
∴ ED∥FB.
