人教版初中数学七年级下册 5.1.1相交线课件(共20张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册 5.1.1相交线课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 914.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
人教版 初中数学
七年级下
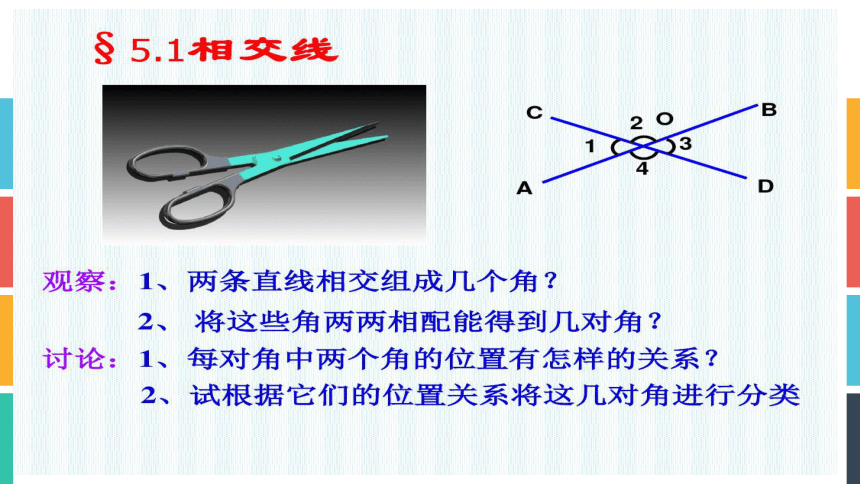
相交线
观察这些图片,你能否看到相交线、平行线?
提出问题
本课是在学生已经学习了直线、射线、
线段和角的有关知识的基础上,进一步研究
平面内不重合的两条直线的一种位置关系:
相交,研究相交线所形成的邻补角、对顶
角的位置和数量关系.
课前了解
5.1.1 相交线
人教版七年级数学 下册
目标导航
1.理解邻补角与对顶角的概念;
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(重点、难点)
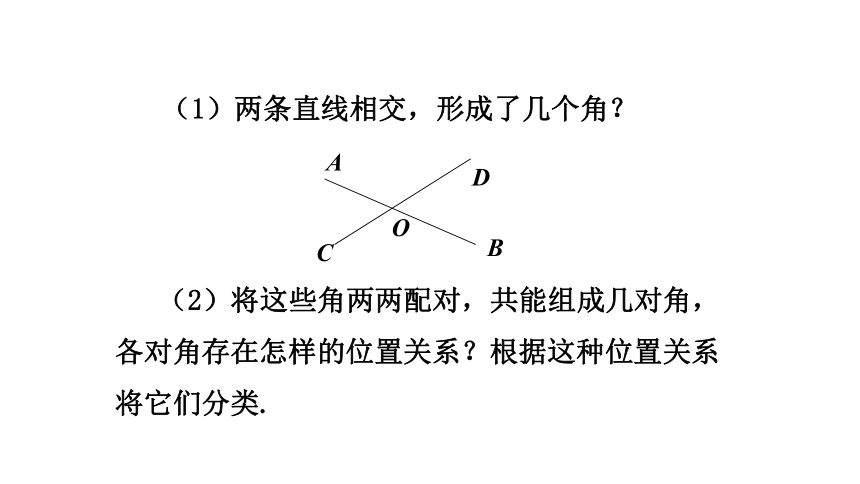
(1)两条直线相交,形成了几个角?
O
C
A
B
D
(2)将这些角两两配对,共能组成几对角,各对角存在怎样的位置关系?根据这种位置关系将它们分类.
1
2
A
C
D
O
3
4
B
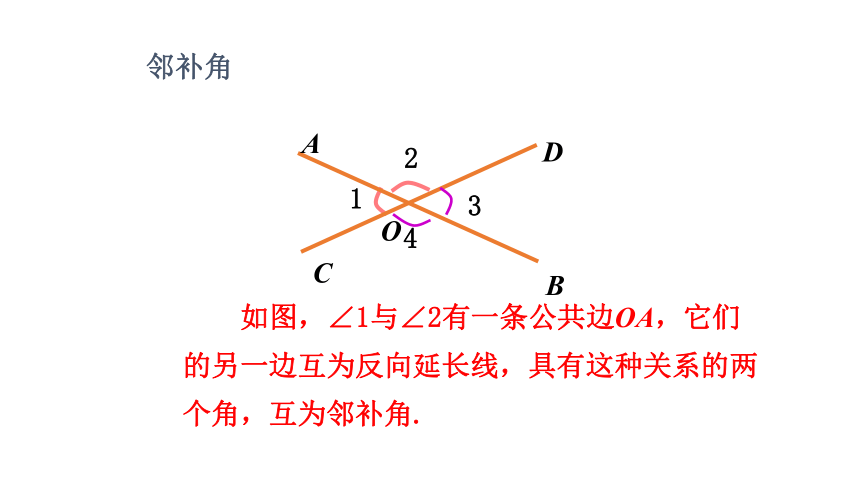
如图,∠1与∠2有一条公共边OA,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角
1
2
3
A
B
C
D
O
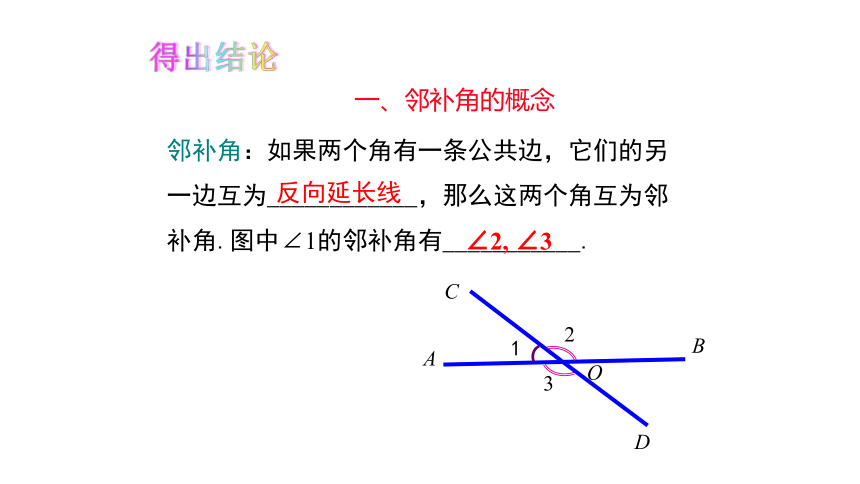
邻补角:如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2, ∠3
一、邻补角的概念
得出结论
1
2
A
C
D
O
3
4
B
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种关系的两个角,互为对顶角.
对顶角
1
2
A
B
C
D
O
对顶角:如果两个角有一个公共定点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
二、对顶角的概念
得出结论
动手练一练
1.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°
∠2+∠3= 180°
∴∠2的补角有∠1和∠3
∵ ∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5
∴∠2的补角有∠6和∠8
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°
∴∠8= ∠1
∵ ∠8= ∠6(对顶角相等)
∴∠6= ∠1.
如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
拓展
观察下列各图,寻找对顶角(不含平角)
⑴ 如图a,图中共有 对对顶角;
⑵ 如图b,图中共有 对对顶角;
⑶ 如图c,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有10条直线相交于一点,则可形成 对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
如图,若∠1:∠2=2:7 ,求各角的度数。
解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°, ∠2=140°
根据对顶角相等,得
∠3=40°, ∠4=140°
下列各图中,∠1和∠2是邻补角吗?
为什么?
(1) (2) (3)
1
2
1
1
2
2
谢谢
人教版 初中数学
七年级下
相交线
观察这些图片,你能否看到相交线、平行线?
提出问题
本课是在学生已经学习了直线、射线、
线段和角的有关知识的基础上,进一步研究
平面内不重合的两条直线的一种位置关系:
相交,研究相交线所形成的邻补角、对顶
角的位置和数量关系.
课前了解
5.1.1 相交线
人教版七年级数学 下册
目标导航
1.理解邻补角与对顶角的概念;
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.(重点、难点)
(1)两条直线相交,形成了几个角?
O
C
A
B
D
(2)将这些角两两配对,共能组成几对角,各对角存在怎样的位置关系?根据这种位置关系将它们分类.
1
2
A
C
D
O
3
4
B
如图,∠1与∠2有一条公共边OA,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
邻补角
1
2
3
A
B
C
D
O
邻补角:如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2, ∠3
一、邻补角的概念
得出结论
1
2
A
C
D
O
3
4
B
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种关系的两个角,互为对顶角.
对顶角
1
2
A
B
C
D
O
对顶角:如果两个角有一个公共定点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
二、对顶角的概念
得出结论
动手练一练
1.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°
∠2+∠3= 180°
∴∠2的补角有∠1和∠3
∵ ∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5
∴∠2的补角有∠6和∠8
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°
∴∠8= ∠1
∵ ∠8= ∠6(对顶角相等)
∴∠6= ∠1.
如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
拓展
观察下列各图,寻找对顶角(不含平角)
⑴ 如图a,图中共有 对对顶角;
⑵ 如图b,图中共有 对对顶角;
⑶ 如图c,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有10条直线相交于一点,则可形成 对对顶角.
图a
图b
图c
2
6
12
n(n-1)
90
如图,若∠1:∠2=2:7 ,求各角的度数。
解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°, ∠2=140°
根据对顶角相等,得
∠3=40°, ∠4=140°
下列各图中,∠1和∠2是邻补角吗?
为什么?
(1) (2) (3)
1
2
1
1
2
2
谢谢
